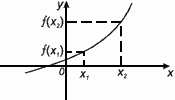Наименование школы
|
СШ №
|
предмет
|
Алгебра
|
ФИО педагога
|
Валиева
|
Дата: урок №»5
|
|
Класс: 10
|
Количество присутствующих: Количество отсутствующих
|
Раздел:
|
10.1А Функция, ее свойства и график
|
Класс:
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Свойства функции
|
Цели обучения в соответствии
с учебной программой
|
10.4.1.3 - уметь определять свойства функции;
|
Цели урока
|
Учащиеся повторят и систематизируют материал по свойствам функции
|
Ход урока
Этап урока/
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Организационный момент
Середина урока
Конец урока
|
. Приветствует учеников, проверяет готовность к уроку, желает успеха.
Фронтальная работа.
№1. По данным рисункам определите:
а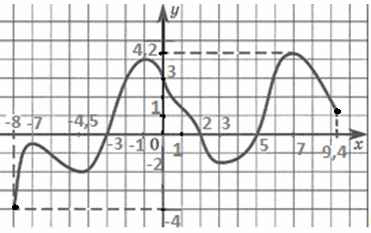 ) область определения функции; ) область определения функции;
б) область значений функции;
в) нули функции;
г) промежутки знакопостоянства функции.
Приложение №1
Групповая работа.
Объедините учащихся в группы. Предложите карточки с графиками нескольких функций для закрепления понятия монотонности на промежутке.
Попросите учащихся определить промежутки возрастания, убывания и постоянства функции. Является ли функция непрерывной?
1. Определите промежутки возрастания, убывания и постоянства функции. Является ли функция непрерывной?
Период функции. рассмотреть различные виды периодических функций и их свойства. Например, функцию y =С, где С-const, периодом которой является любое число
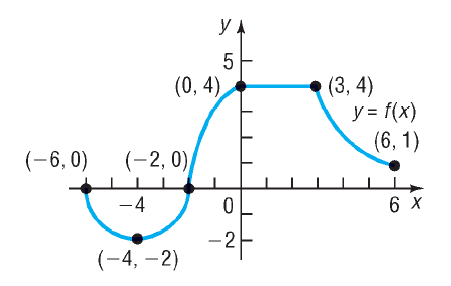 T ≠ 0 и функцию дробной части числа T ≠ 0 и функцию дробной части числа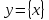 , где периодом будетT =1. , где периодом будетT =1.
Индивидуальная работа.
1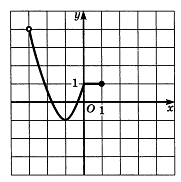 . Функция, имеющая период Т = 4 задана графиком на промежутке (-3;1]. Найдите значение этой функции при х = 11. . Функция, имеющая период Т = 4 задана графиком на промежутке (-3;1]. Найдите значение этой функции при х = 11.
Задание.Определите по заданному графику функции её свойства.
Четность функции. Приложение №2
П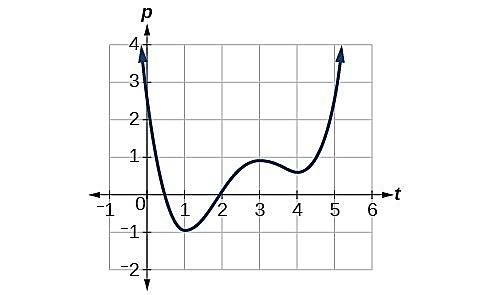 ри исследовании функции на четность и нечетность можно использовать следующие свойства: ри исследовании функции на четность и нечетность можно использовать следующие свойства:
Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
Произведение двух четных функций является четной функцией, равно как и произведение двух нечетных функций. Произведение четной и нечетной функции — нечетная функция.
Если функция  четная (нечетная), то и обратная функция четная (нечетная), то и обратная функция  четная (нечетная). четная (нечетная).
Задание. Исследуйте функцию 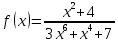 на четность. на четность.
Рефлексия.
Рефлексия
В конце урока учащиеся проводят устную рефлексию (по желанию):
– Я понял, что …
– Я узнал, что …
– Я научился …
Домашнее задание.
|
Совместно с учащимися определяют тему и цель урока.
Совместно с учителем повторяют свойства функции.
Повторяют определения.
Записывают ответы на вопросы
а)
б)
в)
г)
Работа с памяткой
Учащиеся самостоятельно выполняют задание с последующей взаимопроверкой в парах. При необходимости получают консультацию учителя.
Выполняют задание.
Определяют
1)область определения функции;
2) область значения функции;
3) нули функции;
4) периодичность функции;
5) промежутки монотонности;
6) промежутки знакопостоянства функции;
7) наибольшее и наименьшее значения функции;
8) четность, нечетность функции;
9) ограниченность функции;
10) непрерывность функции;
11) экстремумы функции
Знакомятся с алгоритмом и свойствами
Выполняют задания. Учащийся у доски
Приложение №3
Учащиеся подытоживают свои знания по изучаемой теме.
|
Словесная оценка учителя.
Взаимооценивание
Словесная оценка учителя.
Взаимооценивание
Взаимопроверка
ФО
самопроверка по образцу, комментарии учителя
Словесная оценка учителя
Взаимооценивание
|
Раздаточный материал
Приложение №1
|
Приложение №1
«Свойства функции»
|
Памятка
|
1. Чётность и нечётность
|
Функция четная, если
f(-x) = f(x)
Св-во: График четной функции симметричен относительно оси 0y
|
Функция нечетная, если
f(-x) = –f(x)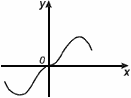
Св-во: График нечетной функции симметричен относительно начала координат.
|
2.Периодичность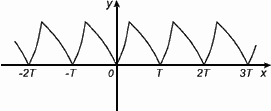
|
Функция f(x) периодическая, если f(x) = f(x+Т) = f(x-Т), 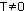 , ,
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
|
3. Монотонность (возрастание, убывание)
|
|
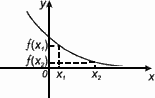
Функция f(x) возрастает, если x1 < x2 и f(x1)< f(x2).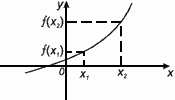
|
Функция f(x) убывает, если x1 < x2 и f(x1) > f(x2).
|
Функция f(x) не возрастает,
если x1 < x2 и f(x1) ≥ f(x2).
|
Функция f(x) не убывает,
если x1 < x2 и f(x1) ≤ f(x2).
|
4. Промежутки знакопостоянства
|
|
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
|
Промежуток, на котором y>0, график находится выше оси ОХ.
Промежуток, на котором y<0, график находится выше оси ОY
|
5.Ограниченность и неограниченность.
|
|
Функция называется ограниченной, если, |f(x)| ≤ b, b>0
|
Если b>0 не существует, то функция - неограниченная.
|
6. Экстремумы
|
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
|
Хmax - точка максимума, если f(х)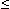 f(Xmax). f(Xmax).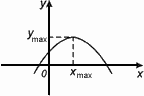
Ymax=f(Xmax) - максимум функции.
|
Хmin - точка минимума, если f(х)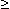 f(Xmin). f(Xmin).
Ymin=f(Xmin) - минимум функции.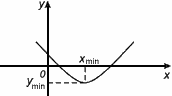
|
Приложение№2
Алгоритм исследования функции на четность
1.Установить, симметрична ли область определения функции. Если нет, то функция ФОВ, если да, то второй шаг
2. Составить выражение f(-x)
3. Сравнить f(-x) и f(x)
а) если f(-x) = f(x), то функция четная
б) если f(-x) = -f(x), то функция нечетная
в) если не а) и б) то ФОВ
Приложение №3
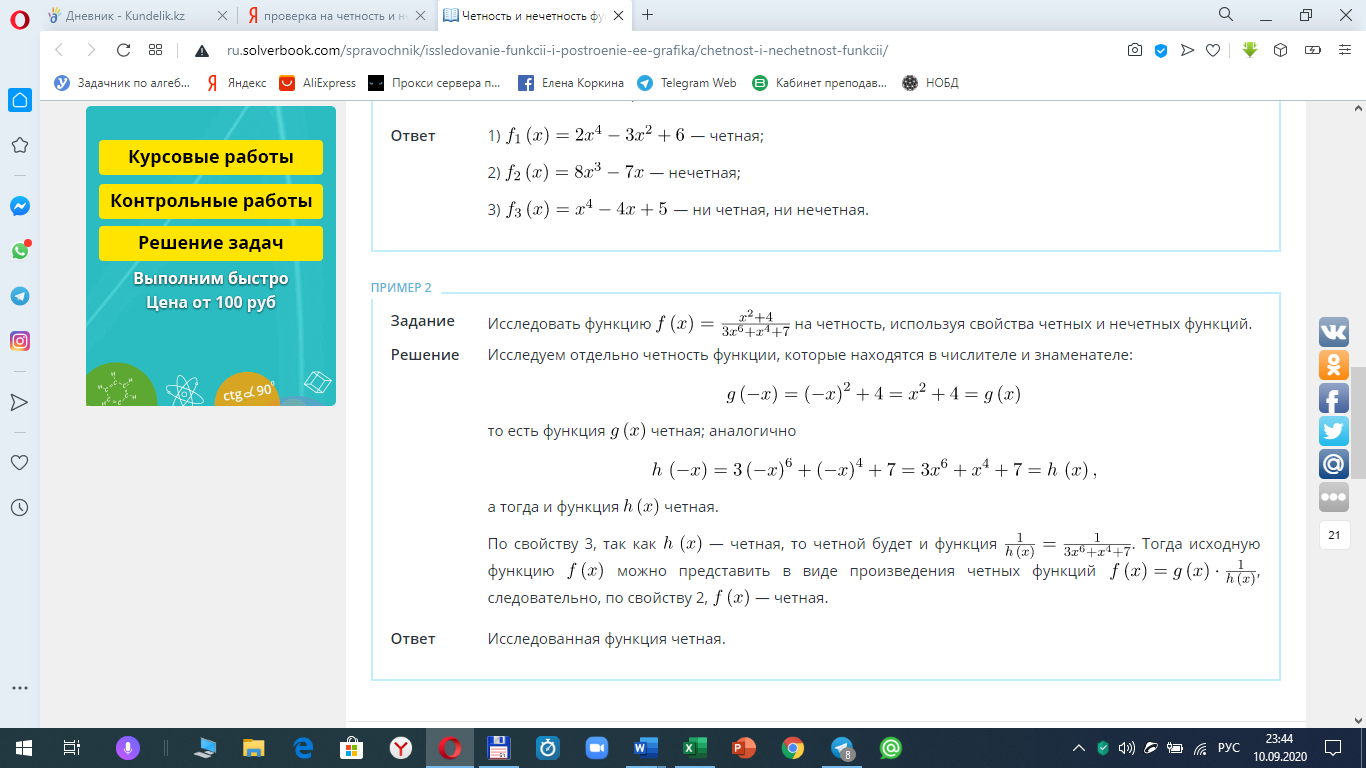
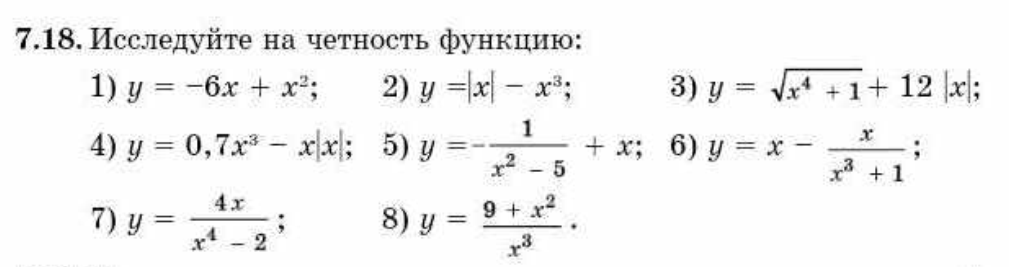 |
 Скачать 438.97 Kb.
Скачать 438.97 Kb.

 ) область определения функции;
) область определения функции; T ≠ 0 и функцию дробной части числа
T ≠ 0 и функцию дробной части числа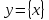 , где периодом будетT =1.
, где периодом будетT =1. . Функция, имеющая период Т = 4 задана графиком на промежутке (-3;1]. Найдите значение этой функции при х = 11.
. Функция, имеющая период Т = 4 задана графиком на промежутке (-3;1]. Найдите значение этой функции при х = 11.  ри исследовании функции на четность и нечетность можно использовать следующие свойства:
ри исследовании функции на четность и нечетность можно использовать следующие свойства: четная (нечетная), то и обратная функция
четная (нечетная), то и обратная функция  четная (нечетная).
четная (нечетная).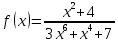 на четность.
на четность.