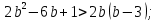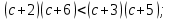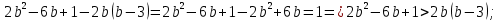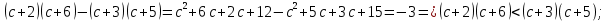Урок №5 Учитель: Зарипова Л.З.
Предмет: Алгебра
Тема урока: Числовые неравенства.
Тип урока: Изучение новой темы.
Цели: расширить представления учащихся о числовых неравенствах; сформировать навыки записи, чтения и сравнения числовых промежутков между собой, развивать умение использовать теоретические знания при решении практических задач, познавательный интерес к математике, расширять кругозор;
Задачи:
Образовательные:
познакомить учащихся с определением неравенств и числовых неравенств;
рассмотреть правила сравнения числовых неравенств;
рассмотреть универсальный способ сравнения;
Развивающие:
развитие логического мышления;
развитие умений анализировать и делать выводы.
Воспитательные:
Методы:
Групповой
Индивидуальный (при построении в тетрадях);
Фронтальный (во время подведения итогов исследовательской работы и итогов урока вообще).
Планируемые результаты обучения:
Личностные:
готовность и способность обучающихся к саморазвитию и личностному самоопределению;
сформированность их мотивации к обучению и целенаправленной познавательной деятельности, системы значимых социальных и межличностных отношений, ценностно-смысловых установок, отражающих личностные и гражданские позиции в деятельности, социальные компетенции, правосознание;
способность ставить цели и строить жизненные планы;
способность к осознанию российской идентичности в поликультурном социуме.
Метапредметные:
самостоятельно определять цели своего обучения;
осуществлять контроль своей деятельности в процессе достижения результата;
соотносить свои действия с планируемыми результатами;
определять способы действий в рамках предложенных условий и требований;
определять понятия;
устанавливать причинно-следственные связи;
понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
действовать в соответствии с предложенным алгоритмом.
Предметные:
повторить правила сравнения чисел;
ввести определение понятия числового неравенства;
формировать умение использовать данное определение для сравнения чисел и доказательства неравенств
расширить знания о числовых неравенствах
познакомиться с ролью неравенств в жизни.
Структура урока:
Организационный этап (3 мин).
Актуализация знаний (5 мин).
Изложение нового материала (20 мин).
Первичное закрепление (15 мин).
Рефлексия (2 мин).
Итог урока, домашнее задание (3 мин).
Оборудование:
Алгебра. 8 класс. Учебник. 2013,2007 год - Макарычев Ю.Н. и др.
Этап урока и его цель
|
Деятельность учителя
|
Деятельность учащихся
|
Формируемые УУД
|
Организационный этап;
Цель: настроить учащихся на урок
|
Учитель приветствует учащихся, проверяет присутствующих, оценивает самочувствие детей.
|
Приветствуют учителя и проверяют свою готовность к уроку.
|
Регулятивные:
учащиеся проверяют свою готовность к уроку.
|
Актуализация опорных знаний. Фронтальный опрос.
Цель: вспомнить пройденный материал.
|
Сегодня мы начинаем изучать новый раздел алгебры, который называется «Неравенства».
В этом разделе мы познакомимся с числовыми неравенствами, их видами и свойствами.
Научимся их применять при сравнении выражений и доказательстве неравенств. И с многим другим интересным материалом входящим в этот раздел.
Ребята, давайте вспомним всё, что мы знаем о сравнении.
Ребята, посмотрите на доску, сравните:
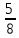 и и 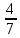
3,6748 и 3,675
36,5810 и 36,581
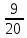 и 0,45 и 0,45
-5,5 и 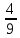
-15 и -23
-115 и -127
Ребята, а какие правила используют для сравнения чисел?
Какое правило применяется для сравнения чисел, расположенных на координатной прямой?
На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.
Действительно, пусть a и b – некоторые числа. Обозначим разность a - b буквой с. Так как а – b= с, то a=b+c.
Если с – положительное число, то точка с координатой b+с лежит правее точки с координатой b, а если с – отрицательное число, то точка левее.
Значит, если а > b, то точка с координатой а лежит правее точки с координатой b, а если a < b – левее.
Заметим!
«В зависимости от конкретного вида чисел используют тот или иной способ сравнения. Что не совсем удобно. Легче иметь универсальный способ сравнения чисел, который мог бы охватить все случаи».
|
Готовятся к уроку. Настраиваются на рабочий лад.
Слушают учителя.
Смотрят на доску и отвечают на вопросы.
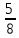 > > 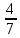
3,6748 < 3,675
36,5810 = 36,581
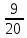 = 0,45 = 0,45
-5,5 < 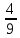
-15 > -23
-115 > -127
Отвечают, какие правила используют для сравнения чисел:
а) Из двух положительных чисел больше то, модуль которого больше;
б) Из двух отрицательных чисел больше то, модуль которого меньше;
в) Любое отрицательное число меньше положительного;
г) Любое положительное число больше нуля;
д) Любое отрицательное число меньше нуля.
Смотрят на доску и вспоминают какое правило применяется для сравнения чисел, расположенных на координатной прямой.
|
Личностные: устанавливают связь учебной деятельности с ее мотивом.
|
Изложение нового материала.
|
Так что же такое неравенство?
Неравенство - соотношение между числами (или любыми математическими выражениями, способными принимать численное значение), указывающее, какое из них больше или меньше другого.
Давайте теперь рассмотрим универсальный способ сравнения:
a>b, a-b>0;
a
a=b, a-b=0;
«Число a больше числа b, если разность a – b – положительное число; число а меньше числа b, если разность a – b – отрицательное число; если разность a – b = 0, то числа а и b равны.»
Рассмотрим пример:
Докажем, что при любых значениях переменной а верно неравенство:
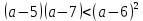
Пример 2.
Докажем что 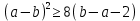 : :
|
Записывают определение.
Записывают способ в тетрадь.
a>b, a-b>0;
a
a=b, a-b=0;
Для этого составим разность левой и правой частей неравенства, и преобразуем её:
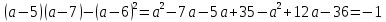
При любом а рассматриваемая разность отрицательна и, следовательно, верно неравенство
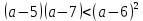
Решают и записывают в тетради пример.
Предположим «противное», то есть, что 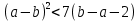 : :
Теперь попробуем это доказать, предварительно раскрыв скобки и перенеся все в левую часть (здесь частично используем метод доказательства по определению):
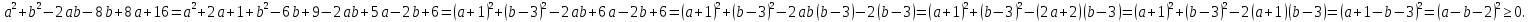
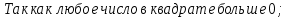
Делаем вывод о том, что наше предположение неверно. Значит, неравенство (a – b)2 ≥ 8(b – a – 2) доказано.
|
Личностные:
осознания качества усвоенных знаний
|
Первичное закрепление Цель: закрепить изученный материал.
|
Итак, теперь давайте откроем рабочие тетради и выполним задания №. 724, 728(а, г), 729(в, г), на страницах 22 – 26, и №12 из учебника на странице15.
(Задание №724. Сравните числа a и b, если:
а) 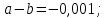
б) 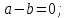
в) 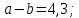
Задание №728. Докажите что при любом значении переменной верно неравенство:
а) 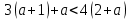 ; ;
г) 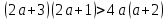
Задание №729. Докажите неравенство:
в) 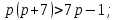
г) 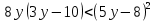 ; ;
|
Выполняют задания на закрепление темы.
Открывают рабочие тетради и выполняют задания:
Задание №724.
а) 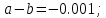
Разность a и b– отрицательна, из этого следует что b > a на -0,001.
б) 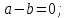
Разность a и b – равна нулю, из этого следует, что a = b.
в) 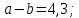
Разность a и b – положительна, из этого следует что число a – больше, числа b на 4,3;
Задание №728.
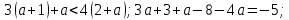 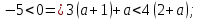
г) 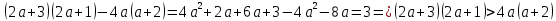
Задание №729.
в)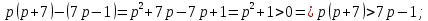
г)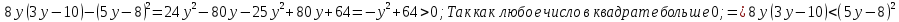 . .
|
Познавательные: проводят анализ и разбор задачи, закрепляют материал.
|
Рефлексия
Цель: проанализировать полученные знания.
|
Как вы можете оценить Вашу работу на нашем занятии по пятибалльной шкале?
Есть ли у Вас вопросы по этой теме, на которые мы не дали ответов?
|
Оценивают уровень знаний по этой теме.
|
|
Итоги урока.
Цель: оценка деятельности учащихся.
|
Учитель сообщает оценки за урок, задает домашнее задание, прощается с классом.
Домашнее задание:
§10. Пункт 28. Номера 728 (б,в) и 729 (а,б).
Все свободны! До свидания!
|
Задание №728(б,в) в РТ.
б) 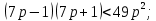
в) 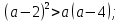
Решение:
б) 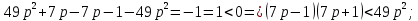
в) 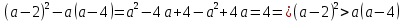 ; ;
Задание №729(а,б) в РТ.
а) 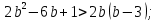
б) 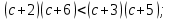
Решение:
а)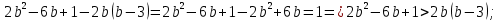
б)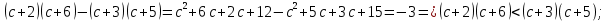
|
| |
 Скачать 33.8 Kb.
Скачать 33.8 Kb.
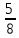 и
и 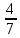
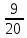 и 0,45
и 0,45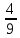
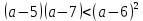
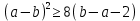 :
: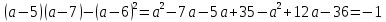
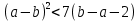 :
: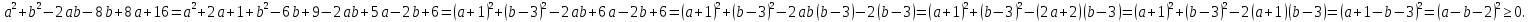
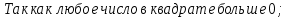
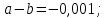
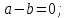
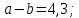
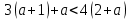 ;
;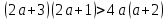
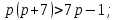
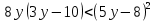 ;
;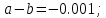
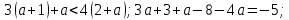
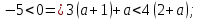
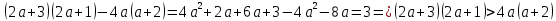
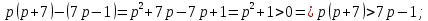
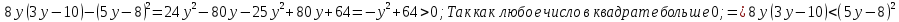 .
.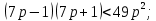
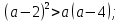
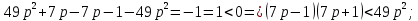
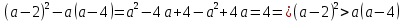 ;
;