21то. Урок. 6 Множества и элементы логики Математическая логика
 Скачать 49.87 Kb.
|
|
Урок. №6 Множества и элементы логики Математическая логика Логика ‑ раздел математики, который изучает доказуемость утверждений. Верные и неверные предложения в математике называют высказываниями. При этом вместо слов «верное» и «неверное» говорят истинное и ложное. Основные операции логики: отрицание, дизъюнкция, конъюнкция. Одним из способов решения логических задач является контрпример — пример, опровергающий верность некоторого утверждения. Множество. Действия над множествами. Множество является первичным неопределяемым понятием в математике. Объекты множества, называются его элементами. Множества обозначаются заглавными буквами, а элементы строчными.  - пустое множество;А∩В - пересечение множеств; АU В ‑ объединение множеств; А∩В =  т.е. нет общих элементов;‑ дополнение; Способы задания множеств. 1. Перечислением его элементов 2. Описание свойств Характеристическое свойство ‑ это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий множеству. Над множествами, как и над числами, выполняют действия. Круги Эйлера ‑ хорошая иллюстрация действий.   Особенно важны числовые множества. N ‑ множество натуральных чисел; Z ‑ множество целых чисел; Q ‑ множество рациональных чисел; R ‑ множество действительных чисел. Математическая индукция Индукцией называется переход от частных утверждений к общим. Одним из важных методов доказательств является метод математической индукции. Большинство формул, относящихся к натуральным числам n, доказываются методом математической индукции.Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если оно справедливо для n = 1 из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1. Доказательство по методу математической индукции проводится в три этапа: Проверятся справедливость утверждения для любого натурального числа n (обычно для n = 1); Предполагается справедливость утверждения при любом натуральном n=k; Доказывается справедливость утверждения для числа nk+1, отталкиваясь от предположения второго пункта. Примеры и разбор решения заданий тренировочного модуля 1. Докажите следующее утвердение: Если n ‑ натуральное число,то число  четное.При n=1 наше утверждение истинно:  четное число.Предположим, что  - четное число.Докажем: - четное. (так как сумма двух четных чисел четное число) Значит, четно при всех натуральных значениях n.2.Задача. Каждый ученик в группе изучает английский или немецкий язык. Английский изучают 25 человек, немецкий 27 человек, а тот и другой 18 человек. Сколько учеников в группе? Решение: А- изучают английский, В ‑ изучают немецкий, А∩В ‑ изучают английский и немецкий. 25+27-18=32 ученика в группе. 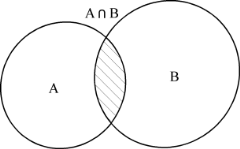 |