Конспект урока по теме: Разложение на множители с помощью формул квадрата суммы и квадрата разности.. Урок 66 Дата 21. 02. 2018 Тема. Разложение на множители с помощью формул квадрата суммы и квадрата разности
 Скачать 20.85 Kb. Скачать 20.85 Kb.
|
|
Урок № 66 Дата 21.02.2018 Тема. Разложение на множители с помощью формул квадрата суммы и квадрата разности. Тип урока: урок проверки и коррекции знаний и умений. Цели урока: Отработать и закрепить навыки разложения многочлена на множители с использованием формул квадрата суммы и квадрата разности, устранить пробелы в знаниях учащихся по использованию данного способа. Развивать логическое мышление, умение применять знания в нестандартных ситуациях, умения классифицировать, обобщать. Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать в коллективе. Формируемые УУД: Личностные: личностное самоопределение; уважительно-доброжелательное отношение к людям. Регулятивные: целеполагание, как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно; планирование, коррекция. Познавательные: умение структурировать знания, контроль и оценка процесса и результата деятельности; анализ, синтез, выбор оснований для сравнения Коммуникативные: речевая деятельность, навыки сотрудничества Основные понятия Многочлен, разложение на множители, формулы сокращенного умножения. Ход урока I. Организационный момент. Мы изучили с вами тему “Возведение в квадрат суммы и разности двух выражений”. На прошлых уроках выяснили, как можно применить эти формулы для разложения многочленов на множители. Сегодня продолжим применение формул квадрата суммы и квадрата разности двух выражений. Как думаете, какая цель сегодняшнего урока? II. Проверка домашнего задания Ответы на вопросы по домашнему заданию (разбор нерешенных задач) № 843 а) (x-8)2≥0 б) (x+4)2≥0 в) -(x+2)2≤0 г) -(x-9)2≤0 №845 а) (x2-4y2)2 б) (  )2 )2в) ( 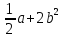 )2 г) (ax-b)2 )2 г) (ax-b)2№851(б) Ответ: 7a3-7a2-15a-a4 Контроль усвоения материала (письменный опрос). Вариант 1. Представьте, если возможно, выражение в виде квадрата одночлена: 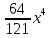 ; 0,36x2y6; 49y10; 4x3 ; 0,36x2y6; 49y10; 4x3Представить в виде удвоенного произведения: 2a; 30b; 4n; 10xy; Разложить на множители трехчлен: b2+10b+25 б. a6-6a3b2 +9b4 Вариант 2. Представьте, если возможно, выражение в виде квадрата одночлена:  ; 0,81x6y8; 64y10; 25x7 ; 0,81x6y8; 64y10; 25x7Представить в виде удвоенного произведения: 4b; 32ab; 2c; 20xy; Разложить на множители трехчлен: а. c2-8c+16 б. x4+2x2y+y2 III. Актуализация опорных знаний: Что значит разложить на множители? Сформулируйте, как возвести в квадрат сумму двух выражений? Сформулируйте, как возвести в квадрат разность двух выражений? IV. Решение упражнений на разложение многочленов на множители с помощью формулы квадрата суммы и квадрата разности №№852 – устно Какое правило применяли для выполнения данного задания? №840 (в) – самостоятельно с проверкой № 844 – в тетрадях, с комментированием № 846 – самостоятельно с проверкой Дополнительное задание Продолжите ряд: 101, 112, 131, 415, 161, 718 ... (поставить запятые через каждые две цифры. Теперь понятно, что следующее число будет 192. Последовательность состоит из чисел 10, 11, 12, и т.д., но запятые расставлены через каждые три цифры). Чему равна сумма -65+(-64)+(-63)+…+64+65+66? V. Итоги урока. Рефлексия: А теперь ребята продолжите предложение: Сегодня на уроке мне понравилось… Сегодня на уроке я повторил… Сегодня на уроке я закрепил… Какие виды работ вызвали затруднения и требуют повторения… В каких знаниях уверен… Помог ли урок продвинуться в знаниях, умениях, навыках по предмету… Кому, над, чем следовало бы ещё поработать… Насколько результативным был урок сегодня. VI. Домашнее задание. №№ 850, 970, 851(в) |
