конспект урока Равенство фигур. Конспект урока по геометрии. Равенство фигур. Равенство треуголь. Урок 9. Понятие о равенстве фигур. Равенство треугольников. 7 класс п онятие о равенстве фигур
 Скачать 1.37 Mb.
|
|
Урок №9. Понятие о равенстве фигур. Равенство треугольников. 7 класс П 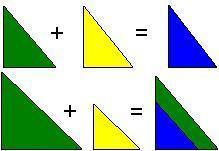 онятие о равенстве фигур1.1.В геометрии две фигуры, имеющие одинаковые форму и размер называют равными. 1.2. Две геометрические фигуры называются равными, если их можно совместить при наложении. Из этого определения 1.1. следует, например, что если заданные прямоугольник и квадрат имеют равные площади, то они всё равно не становятся равными фигурами, так как это разные фигуры по форме. Или, два круга однозначно имеют одну и ту же форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры. Вопрос: Какие отрезки будут считаться равными? Какие окружности будут считаться равными? Какие прямоугольники будут считаться равными? Ответ: Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами (короткая сторона одного прямоугольника равна короткой стороне другого, длинная сторона одного прямоугольника равна длинной стороне другого). На глаз бывает трудно определить, равны ли фигуры, имеющие одинаковую форму. Поэтому для определения равенства простых фигур их измеряют (с помощью линейки, циркуля). У отрезков длину, у кругов радиус, у прямоугольников длину и ширину, у квадратов только одну любую сторону. Вопрос: Можно ли сравнивать все геометрические фигуры? Ответ: Тут следует отметить, что не все фигуры можно сравнивать. Нельзя, например, определить равенство прямых, т. к. любая прямая бесконечна, и , следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца. Если же мы имеем дело со сложными (произвольными) фигурами, то бывает даже сложно определить, имеют ли они одинаковую форму. Ведь фигуры могут быть перевернуты в пространстве. Трудно сказать, одинаковые ли это по форме фигуры или нет.  Таким образом, нужно иметь надежный принцип сравнения фигур . Он таков: равные фигуры при наложении друг на друга совпадают. Чтобы сравнить две изображенные фигуры наложением, на одну из них накладывают кальку (прозрачную бумагу) и копируют (срисовывают) на нее форму фигуры. Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать. Если можно вырезать сами фигуры (или они представляют собой отдельные плоские объекты, а не нарисованы) то калька не нужна. П  ри изучении геометрических фигур можно заметить множество их особенностей, связанных с равенством их частей. Так, если сложить круг вдоль диаметра, то две его половинки окажутся равными (они совпадут наложением).  Если разрезать прямоугольник по диагонали, то получится два прямоугольных треугольника. Если один из них повернуть на 180 градусов по часовой стрелке или против часовой стрелки, то он совпадет со вторым. То есть диагональ разбивает прямоугольник на две равные части. Равенство треугольников  А.Д. Александров Геометрия 7 класс А сейчас выполним задание поэтапно: 1  .Начертим два равных угла. Этот способ построения угла равного данному углу, мы выбрали не случайно. Обратите внимание: в результате построения у нас получилось два треугольника с равными сторонами: АВ=ON=AC=OM=R , BC=NM по построению. А теперь измерьте углы между соответствующими равными сторонами. Получили, что < А= < О, < В= Делаем выводы: Значит, в равных треугольниках соответствующие углы равны. Выполним самостоятельно: Проведем прямую а и в Отметим на них точки А и В, Р и С соответственно так, чтобы расстояние между точками на одной прямой было 4 см. От точки А и Р с помощью транспортира против часовой стрелки по отношению к прямым а и в откладываем <60о , а от точек В и С аналогично <130о. Продолжим лучи, образующие углы до пересечения прямых.     Е К А 4 см В Р 4 см С Полученные лучи пересекаются в точках Е и К Измерим стороны АЕ и РК, ВЕ и КС, они равны.  Мы доказали, что если у двух треугольников два угла равны , прилегающие к равным сторонам, то у них и две другие стороны равны. Аналогично докажем, что если построить два равных угла, и, на лучах, образующих эти углы отложить равные отрезки соответственно, а затем соединить концы отложенных отрезков, то поучим треугольники с равными сторонами. 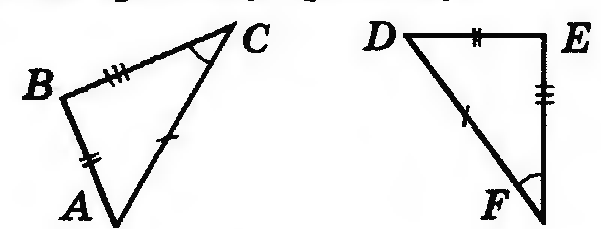 Таким образом, практическим путем, мы доказали три признака, по которым можно определить равенство треугольников. Признаки равенства треугольников — это теоремы, на основании которых можно доказать, что некоторые треугольники равны. В геометрии используются три признака равенства треугольников Первый признак равенства треугольников (по двум сторонам и углу между ними) 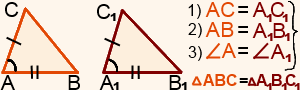 Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников (по стороне и двум прилежащим к ней углам) 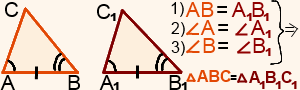 Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Третий признак равенства треугольников (по трем сторонам) 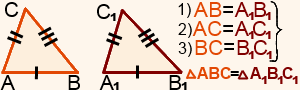 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Домашнее задание ( работа по карточкам): Карточка 1 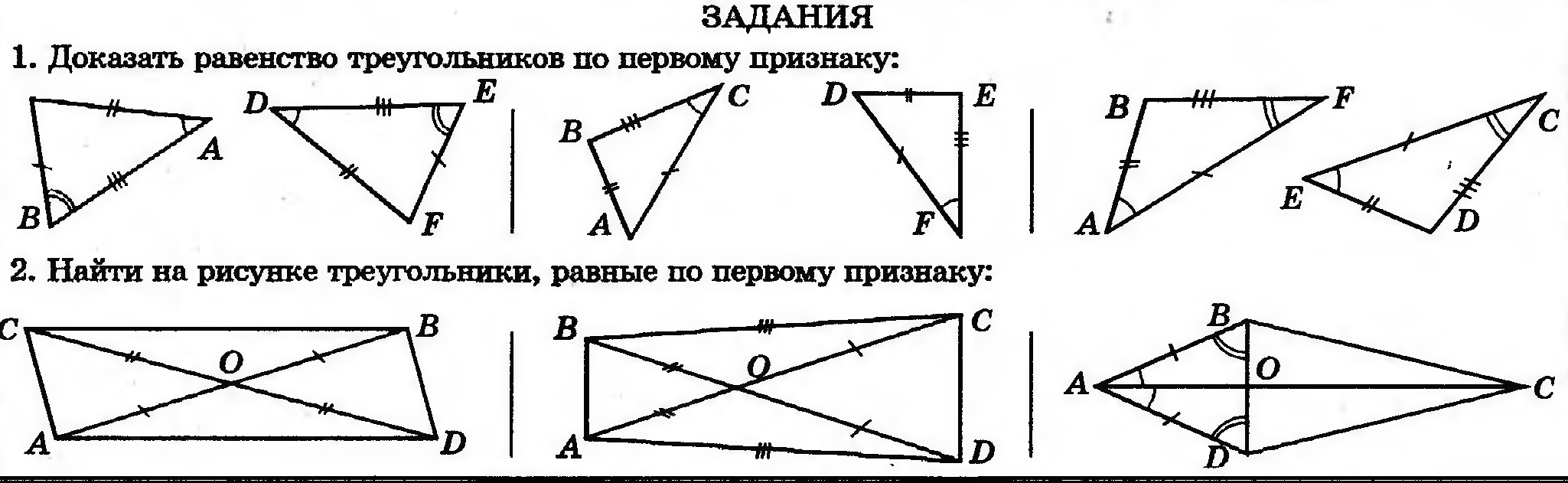 Карточка 2  Карточка 3  |