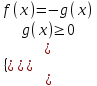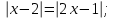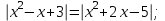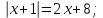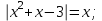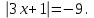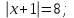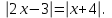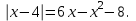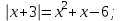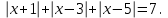|
|
Технологическая карта урока 11 класс. ТК 10.04.2019 алгебра 11 уу. Урок 99 Класс 11б предмет Алгебра и начала математического анализа оу мкоу Троицкая сош
Схема конспекта урока
Часть 1.
Дата 10.04.2019
|
Урок № 99
|
Класс 11Б
|
Предмет Алгебра и начала математического анализа
|
ОУ МКОУ «Троицкая СОШ»
|
Тема урока: Уравнения и неравенства с модулями
|
УМК С.М. Никольский «Алгебра и начала математического анализа»
|
Место урока в системе уроков по теме (всего уроков на тему/номер урока по теме): № 1/1
|
Тип урока: комбинированный
|
Дидактические единицы учебного материала, которыми ученик должен владеть для успешной работы на уроке
|
Дидактические единицы учебного материала, которые ученик изучит на уроке
|
Представлять, понимать
|
Знать
|
Уметь
|
Алгоритм: решение уравнений и неравенств с модулями
|
Модуль числа
|
Определение модуля
|
Решать простейшие уравнения и неравенства с модулями
|
Планируемые предметные результаты урока
|
Ученик должен знать
|
Ученик должен уметь
|
Ученик научится представлять и понимать
|
На 3
|
На 4
|
На 5
|
На 3
|
На 4
|
На 5
|
Хотя бы один способ решения для одного из видов уравнений и неравенств
|
Способ решения для двух из видов уравнений и неравенств
|
Все способы решения для всех видов уравнений и неравенств
|
Решать хотя бы один из видов уравнений и неравенств
|
Решать два вида уравнений и неравенств
|
Решать все виды уравнений и неравенств
|
Алгоритм решения уравнений и неравенств, содержащий знак модуля
|
Метапредметная направленность урока заключается в формировании умения осуществлять поиск решения задачи посредством организации деятельности учащихся по анализу условия, составлению плана решения.
|
|
Личностная направленность урока заключается в формировании ответственного отношения к делу посредством организации деятельности учащихся по осуществлению поиска решения задач.
|
|
Технология обучения
|
Форма обучения
|
Метод обучения
|
Системно-деятельностный подход
|
Фронтальная, индивидуальная, групповая, парная
|
практикум
|
Дидактические средства обучения
|
Презентация, карточки
|
Источники информации:
|
для учителя
|
для обучающихся
|
Никольский С.М., Потапов М.К., Н.Н. Решетников Н.Н., Шевкин А.В. Алгебра и начала математического анализа, учебник для 11 класса общеобразовательных учреждений, М.: Просвещение, 2009.
Дорофеев Г. В. Обобщение метода интервалов. – Математика в школе, 1969, №3.
Панферов В. С., Сергеев И. Н. ЕГЭ – 2010. Математика. Задача С3, под редакцией А. Л. Семенова и И. В. Ященко. – М.: МЦНМО, 2010.
Садовничий Ю. В. ЕГЭ. Практикум по математике: Решение уравнений и неравенств. Преобразование алгебраических выражений. – М.: Издательство «Экзамен», 2012.
|
Презентация, карточки
|
Цель урока:
(определяется планируемыми результатами и способами их достижения)
|
Задачи урока:
(конкретизация цели)
|
Способствовать формированию у учащихся умений решать уравнения и неравенства, содержащие знак модуля
|
1) формирование у учащихся умения отбирать нужную информацию для изучения темы (фронтальный опрос);
2) формирование у учащихся умения формулировать тему и цель урока (фронтальная работа по вопросам учителя);
3) формирование у учащихся умения анализировать и обобщать при решении задач;
4) формирование у учащихся умения осуществлять поиск решения задачи по данной теме;
5) формирование у учащихся способности к самоанализу и рефлексии.
|
Часть 2.
Характеристики этапов урока
|
|
|
|
|
|
|
Этап урока, время
|
Цели этапа
|
Предметные учебные действия, формируемые на этапе
|
Универсальные учебные действия, формируемые на этапе
|
ФОУД
|
Используемые на этапе СО
|
1.Актуализация знаний, 10 мин
|
вспомнить ранее изученное (обобщенный метод интервалов, метод рационализации)
|
Уметь использовать знания об обобщенном методе интервалов и методе рационализации
|
Структурирование знаний; выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения
|
ИФ
|
Презентация,
|
2. Изучение нового материала, 10 мин
|
Формировать у учащихся основные понятия по данной теме; знакомство с алгоритмом решения уравнений и неравенств с модулями
|
Алгоритм решения уравнений и неравенств со знаком модуля
|
Понимание и осмысление информации
|
Ф
|
Презентация
|
3.Закрепление знаний, 17 мин
|
формирование умения выполнять анализ задач через фронтальную работу с классом;
формирование умения составлять план решения задач;
формирование умения реализовывать план решения задач через самостоятельную работу.
|
Умение решать уравнения и неравенства, содержащие знак модуля
|
Умение составлять план действий
|
Ф П И
|
Презентация, карточки
|
4.Рефлексия
|
оценить удовлетворенность уроком
|
|
Умение выражать свои мысли
|
Ф
|
Лист рефлексии
|
5.Подведение итогов урока, домашнее задание 3 мин
|
подвести итоги урока, запись домашнего задания
|
|
Умение анализировать и оценивать свою деятельность
|
Ф
|
Лист самооценки
|
Характеристики этапов урока
|
|
|
|
Этап урока, время
|
Деятельность учителя
(с указанием конкретных методов и приемов обучения, средств и форм контроля, учебно-познавательных и учебно-практических задач, решаемых на данном этапе)
|
Деятельность учащихся
|
Продукт деятельности учащихся
|
1.Актуализация знаний, 10 мин
|
Учитель проводит фронтальный опрос, предлагает учащимся подумать над тем, какую деятельность они чаще всего осуществляют на уроках математики, в результате чего формулируется цель урока.
|
Учащиеся отвечают на вопросы
|
Ответы на вопросы учителя
|
2. Изучение нового материала, 10 мин
|
Объясняет новый материал в виде лекции. К каждому утверждению приводит примеры и вместе с учащимися разбирает их решение. После совместно с учащимися обобщают то, о чем было рассказано.
|
Слушают объяснение учителя, делают необходимые записи в тетради, участвуют в разборе примеров. Отвечают на вопросы учителя.
|
Конспект в тетради
|
3.Закрепление знаний, 17 мин
|
Осуществляет дифференцированную работу по закреплению полученных знаний, а именно, организует работу у доски по решению уравнений и неравенств с модулями
|
Решают задания у доски, отвечают на вопросы учителя. Обосновывают свой ответ. Участвуют в обсуждении выявленных затруднений.
|
Решенные задания, карточка
|
4.Рефлексия
|
Учитель организует рефлексивную деятельность учащихся
|
Учащиеся оценивают свою деятельность
|
|
5.Подведение итогов урока, домашняя работа, 5 мин
|
Подводит итог урока, обращает внимание учащихся на важные моменты, задает домашнее задание
|
Учащиеся оценивают свою деятельность
|
|
Часть 3.
Ход урока
1. Актуализация знаний
Сообщение темы, цели, задач урока.
Учитель зачитывает слова:
«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
Альберт Эйнштейн
Учащиеся делятся на группы по 4-5 человек для решения и быстрого обсуждения следующих заданий:
Что такое модуль?
Как решаются уравнения: 1) 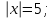 3) 3) 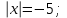
2) 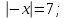 4) 4) 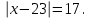
Когда простейшие уравнения имеют один, два, другое число корней?
После работы в группах, общее обсуждение класса.
Проверка ответов учащихся по готовым ответам
Изучение нового материала
Для ознакомления с новым материалом все учащиеся получают следующую вспомогательную тавлицу:
Данные таблицы изучаются учащимися самостоятельно, затем коллективно обсуждается метод решения каждого уравнения из 4 строки.
Виды уравнений
|
Способы решения
|
Особенности решения
|
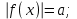
где a 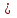 R R
|
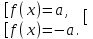
|
Обратить внимание на значение а. Если а<0, то уравнение корней не имеет.
|
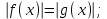
|
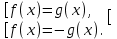
Или f2(x)=g2(x)
|
Совокупность уравнений удобно применять, если подмодульные выражения выше первой степени.
|
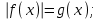
|
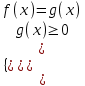 и и 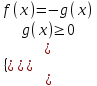
|
Обратить внимание!
После решения уравнений в системе исключить те корни, которые не входят в решение неравенства.
|
Рассмотрите уравнения и определите метод решения с помощью данных таблицы:
а) 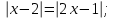
б) 
в) 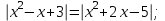
г) 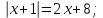
д) 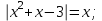
е) 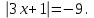
|
Учитель показывает на доске решение уравнения, содержащее переменную под знаком модуля методом промежутков.
Уравнение вида 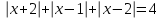 решается с использованием следующего алгоритма: решается с использованием следующего алгоритма:
выражение, содержащееся под знаком модуля, приравниваем к нулю и решаем уравнение;
используя найденные корни, разбиваем числовую ось на промежутки;
исходное уравнение решаем для каждого промежутка по отдельности, причем знак абсолютной величины опускаем на основе определения модуля;
проверяем принадлежность решения рассматриваемому промежутку;
найденные решения уравнений будут корнями исходного уравнения.
Решение уравнения: 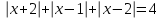
Приравниваем к нулю выражения, стоящие под знаком модуля
х+2=0; х-1=0; х-2=0;
х=-2 х=1 х=2
Найденными корнями разбиваем числовую ось на промежутки
    
х+2 - + + +
х-1 - -2 - 1 + 2 + Х
х-2 - - - +
3,4)) Последовательно исследуем каждое уравнение на каждом
промежутке на «знак» и решаем для каждого промежутка
в отдельности, опуская знак модуля,
затем проверяем принадлежность решения
рассматриваемому промежутку, т.е.
х 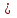 (-∞; -2] (-∞; -2]
-х-2-х+1-х+2 =4
-3х=3
х=-1
х=-1 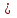 (-∞; -2) - не корень уравнения; (-∞; -2) - не корень уравнения;
х 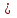 ( -2; 1) ( -2; 1)
х+2-х+1-х+2=4
-х=-1
х=1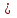 [ -2; 1) – не корень уравнения; [ -2; 1) – не корень уравнения;
х 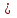 [1; 2) [1; 2)
х+2+х-1-х+2=4
х=1
х=1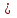 [ 1; 2) – корень уравнения; [ 1; 2) – корень уравнения;
х 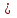 [ 2; +∞) [ 2; +∞)
х+2+х-1+х-2=4
3х=5
х=5/3
х=5/3 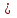 [2;+∞) - не корень уравнения; [2;+∞) - не корень уравнения;
Ответ: 1.
Закрепление изученногоПервичное
Самостоятельная работа в трех разноуровневых вариантах с последующей самопроверкой по готовым ответам. Все ученики получают одинаковые карточки и сами выбирают вариант для работы.
Самостоятельная работа
Тема: Решение уравнений, содержащих переменную под знаком модуля.
|
Самостоятельная работа
Тема: Решение уравнений, содержащих переменную под знаком модуля.
|
Вариант 1 (3 балла)
Решите уравнения:
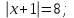
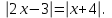
|
Вариант 1 (3 балла)
Решите уравнения:
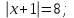
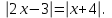
|
Вариант 2 (4 балла)
Решите уравнения:

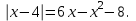
|
Вариант 2 (4 балла)
Решите уравнения:

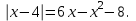
|
Вариант 2 (5 баллов)
Решите уравнения:
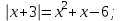
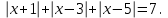
|
Вариант 2 (5 баллов)
Решите уравнения:
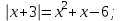
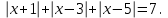
|
Ответы: Вариант 1 Вариант 2 Вариант 3
7 и -9; 1. 4; 3 и  ; 1. -3 и 3 ; 1. -3 и 3
-1/3 и 7. 2. 3 и 4. 2. 2 и 4.
4. Рефлексия
Продолжить фразы на стикерах:
Сегодня я узнала.....
Я смог.....
Я понял, что.....
Я научился.......
Было интересно.......
У меня получилось......
Подведение итогов, домашнее задание
§ 22 № 366(2;4) № 369 (2). (учебник издательства «Мектеп») |
|
|
 Скачать 88.73 Kb.
Скачать 88.73 Kb.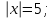 3)
3) 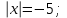
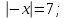 4)
4) 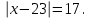
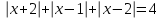 решается с использованием следующего алгоритма:
решается с использованием следующего алгоритма: 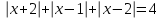





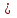 (-∞; -2]
(-∞; -2] 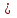 (-∞; -2) - не корень уравнения;
(-∞; -2) - не корень уравнения;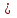 ( -2; 1)
( -2; 1)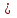 [ -2; 1) – не корень уравнения;
[ -2; 1) – не корень уравнения;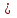 [1; 2)
[1; 2)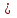 [ 1; 2) – корень уравнения;
[ 1; 2) – корень уравнения;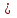 [ 2; +∞)
[ 2; +∞)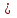 [2;+∞) - не корень уравнения;
[2;+∞) - не корень уравнения; ; 1. -3 и 3
; 1. -3 и 3
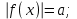
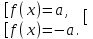
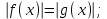
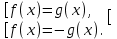
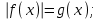
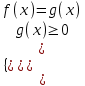 и
и