конспект урока Числовые последовательности. Урок алгебры в 9 классе по теме Числовые последовательности
 Скачать 0.93 Mb.
|
|
Урок алгебры в 9 классе по теме «Числовые последовательности» Цели уроков: Формирование представления о числовой последовательности как функции с натуральным аргументом. Формирование знаний о способах задания числовых последовательностей, умений находить члены последовательности по предложенной формуле, а также умений находить саму формулу, задающую последовательность. Развитие умений применять ранее изученный материал. Развитие умений анализировать, сравнивать, обобщать. Привитие санитарно-гигиенических навыков, пропаганда здорового образа жизни. Ход уроков Организационный момент. Повторение видов функций. Подготовка к восприятию новых знаний. Изучение нового материала. Закрепление. Знаменитые последовательности. Дополнительные задачи. Домашнее задание. Подведение итогов урока. Оборудование и материалы. Рабочий лист для учащихся с планом уроков и упражнениями. Приложение 1. Лист с домашней работой. Приложение 2. Мультимедийный проектор. Экран. Презентация. Урок 1. 1. Организационный момент. Последовательность - одно из самых основных понятий математики. Последовательность может быть составлена из чисел, точек, функций, векторов и т.д. Сегодня на уроке мы познакомимся с понятием " числовая последовательность", узнаем, какие могут быть последовательности, познакомимся со знаменитыми последовательностями. 2. Повторение видов функций. Вам известны функции, определённые на всей числовой прямой или на её непрерывных промежутках: линейная функция у = кх+в, квадратичная функция у = ах2+вх+с, функция у =  ,прямая пропорциональность у = кх, обратная пропорциональность у =  ,кубическая функция у = х3, функция у =|х|.  (Графики функций показываются на слайдах презентации). Для каждой функции указать область определения и способы задания функции. 3. Подготовка к восприятию новых знаний. Но бывают функции, заданные на других множествах. Пример. Во многих семьях есть обычай, своего рода ритуал: в день рождения ребёнка родители подводят его к дверному косяку и торжественно отмечают на нём рост именинника. Ребёнок растёт, и на косяке с годами возникает целая лесенка отметок. Три, пять, два: Такова последовательность приростов от года к году. Но есть и другая последовательность, и именно её члены аккуратно выписывают рядом с засечками. Это - последовательность значений роста. Слайд презентации. Две последовательности связаны друг с другом. Вторая получается из первой сложением. Рост - это сумма приростов за все предыдущие годы. Рассмотрим ещё несколько задач. Задача 1. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день? (Ответы учащихся записываются на доске: 500, 530, 560, 590, 620). Задача 2. В период интенсивного роста человек растёт в среднем на 5 см в год. Сейчас рост у ученика С. - 180 см. Какого роста он будет в 2018 году? (2м 30 см). Но этого быть не может. Почему? Задача 3. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих. Через сколько дней заболеют все ученики нашей школы (300 человек)? (Через 4 дня). Это примеры функций, заданных на множестве натуральных чисел-числовые последовательности. Ставится цель урока: Найти способы нахождения любого члена последовательности. Задачи урока: Выяснить, что такое числовая последовательность и как задаются последовательности. Изучение нового материала. Определение: Числовая последовательность- это функция, заданная на множестве натуральных чисел (слайд: последовательности составляют такие элементы природы, которые можно пронумеровать). Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности: 1, 2, 3, 4, 5, : - последовательность натуральных чисел; 2, 4, 6, 8, 10, :- последовательность четных чисел; 1, 3, 5, 7, 9, : - последовательность нечетных чисел; 1, 4, 9, 16, 25, : - последовательность квадратов натуральных чисел; 2, 3, 5, 7, 11, : - последовательность простых чисел; 1,   ,  ,  , :- последовательность чисел, обратных натуральным.Число членов каждого из этих рядов бесконечно; первые пять последовательностей - монотонно возрастающие, последняя - монотонно убывающая. Обозначение: у1, у2, у3, у4, у5,: 1, 2, 3, 4, 5, :п,:-порядковый номер члена последовательности. (уп)- последовательность, уп- п-ый член последовательности. (ап)- последовательность, ап - п-ый член последовательности. ап-1 -предыдущий член последовательности, ап+1 - последующий член последовательности. № 332. Последовательности бывают конечными и бесконечными, возрастающие и убывающие. Задание. Записать первые 5 членов последовательности: От первого натурального числа увеличение на 3. От 10 увеличение в 2 раза и уменьшение на 1. От числа 6 чередовать увеличение на 2 и увеличение в 2 раза. Эти числовые ряды тоже называются числовыми последовательностями. 5. Знаменитые последовательности: Числа Фибоначчи. Приложение 3. Треугольник Паскаля. Приложение 3. Урок 2. Числовая последовательность считается заданной, если указан способ, позволяющий найти член последовательности любого номера. 1. Способы задания последовательностей: Словесный. (уп)- последовательность натуральных чисел, кратных трём. (уп): 3, 6, 9, 12, 15, : Табличный. Слайд презентации.
Графический. Слайд презентации. Аналитический. Указать формулу п-ого члена последовательности. (уп = 3п) Рекуррентный (от латинского - возвращаться). Это формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие. (уп = уп-1 + 3). 2. Закрепление. сп =  . Запишите первые 5 членов последовательности.(По одному человеку решают у доски, остальные - в тетради). : 74, 81, 88, 95, 102, : Задайте формулу п-ого члена. (уп = уп-1 + 7). Рабочая тетрадь: с. 46, № 38. 3. Дополнительные задачи. Запишите первые пять членов последовательности, заданной таким описанием: каждый член последовательности на 1 больше соответствующего члена ряда Фибоначчи. Запишите первые пять членов последовательности, заданной формулой ап = (-3)п-1. Запишите первые пять членов последовательности, заданной рекуррентно: а1 = 4, ап+1 = ап + 2. Запишите первые пять членов последовательности, заданной графиком: Домашнее задание. Приложение 2. Подведение итогов урока. Итак, мы разобрали понятие последовательности и способы её задания. Ответьте на вопросы: Что такое последовательность? Какие виды последовательностей вы узнали? Какие способы задания вы узнали? О каких ученых и их трудах вы узнали? Литература. О.В. Занина , И.Н. Данкова. Поурочные разработки по алгебре. 9 класс. Л.А. Тапилина, Т.Л. Афанасьева. Алгебра. 9 класс. Поурочные планы. Энциклопедический словарь юного математика. Материалы Фестиваля педагогических идей "Открытый урок": А.А.Болбас. Урок алгебры по теме "Числовые последовательности". 9 класс. А.В. Худякова. Урок по алгебре для 9 класса по теме "Последовательности и способы их задания". Е.Е. Журавлёва. Урок-лекция в 9 классе на тему "Последовательности, понятие, определение. Возрастающие и убывающие последовательности. Способы задания последовательности". Г.А. Бархатова. Интегрированный урок математики и валеологии на тему "Прогрессия". Решение прикладных задач. К. Кноп. "Трактат о кроликах, рождающих великие открытия". Г.И. Глейзер. История математики в средней школе. Ю.В. Пухначев, Ю.П. Попов. Математика без формул. Приложение 1. Лист для учащихся. Тема уроков «ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ». План 1 урока. Повторение видов функций, определение функций, область определения функций. 2. Устное решение задач. Задача 1. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день? Задача 2. В период интенсивного роста человек растёт в среднем на 5 см в год. Сейчас рост у ученика С. – 180 см. Какого роста он будет в 2018 году? Задача 3. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих. Через сколько дней могут заболеть все ученики нашей школы? 3. Определение числовой последовательности. 4. Обозначение. 5. Виды последовательностей. Задание 1. Записать первые пять членов последовательностей: От первого натурального числа увеличение на 3. 2. От 10 увеличение в 2 раза и уменьшение на 1. 3. От числа 6 чередовать увеличение на 2 и увеличение в 2 раза. 6. Знаменитые последовательности: Числа Фибоначчи. Треугольник Паскаля. План 2 урока. 1  . Способы задания последовательностей:Словесный. (уп) – последовательность натуральных чисел, кратных трём. Табличный.
Графический. Аналитический. Рекуррентный (от латинского - возвращаться). 2. Решение упражнений. 1) сп =  . Запишите первые 5 членов последовательности.2) …74, 81, 88, 95, 102,… Задайте формулу п- ого члена последовательности. 3) Рабочая тетрадь: с. 46, № 38. Приложение 2 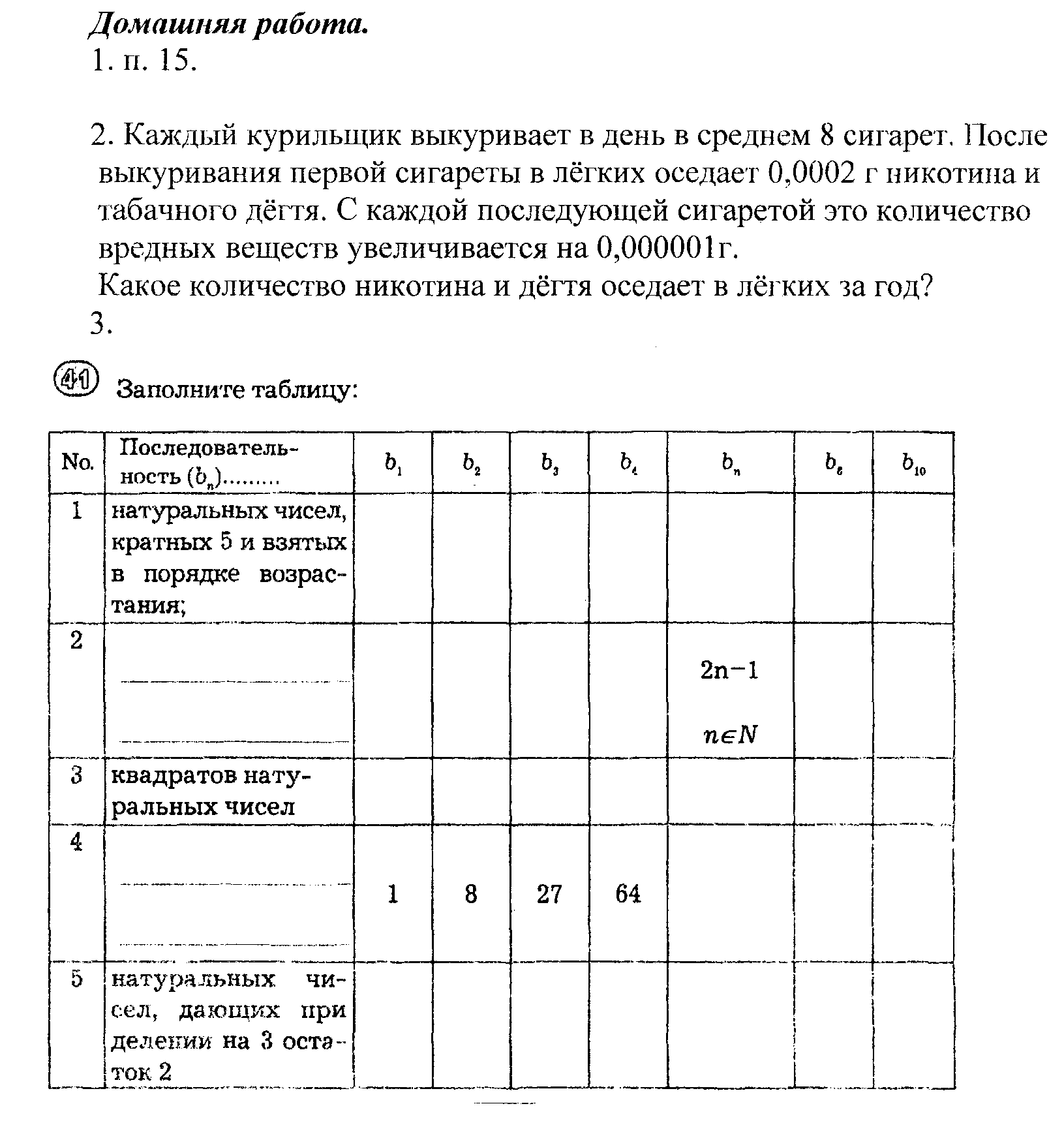 П  риложение 3.ЧИСЛА ФИБОНАЧЧИ. Леонардо Фибоначчи (1180-1240). Слайд презентации. Крупный итальянский математик, автор «Книги абака». Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!). Но по иронии судьбы до нашего времени сохранилась память только об одной задаче из этой книги. Некто поместил пару кроликов в некоем месте, огражденном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производила на свет другую пару, а рождают кролики со второго месяца после своего рождения. (Слайд презентации). Именно в этой задаче появляется последовательность, обессмертившая имя Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … В этой последовательности сумма любых двух предыдущих чисел равна следующему числу: 1+2=3, 3+5=8, 5+8=13,… .Отношение любого числа последовательности к предыдущему колеблется вокруг значения, которое ещё в древности под названием золотого сечения: 1,61803398… «Золотое сечение» определяется как такое положительное число, которое на единицу больше обратного к нему числа: t -  = 1. «Золотое сечение», как идеальная и приятная глазу пропорция человеческого тела и его элементов, широко использовалось многими художниками, начиная с другого великого Леонардо – Леонардо да Винчи. Слайд презентации.Много интересного в арифметики чисел Фибоначчи. Каждое третье число Фибоначчи чётно, каждое четвёртое делится на три, каждое пятнадцатое оканчивается нулём, два соседних числа взаимно просты. Число ап делится на число актогда и только тогда, когда п делится на к. ТРЕУГОЛЬНИК ПАСКАЛЯ. Это бесконечная числовая таблица треугольной формы, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ними слева и справа в предыдущей строке. Блез Паскаль (1623-1662) один из самых знаменитых людей в истории человечества.  В такой форме треугольник Паскаля приведён в «Трактате об арифметическом треугольнике», опубликованном в 1665 г., уже после смерти автора. Слайд презентации Популярность чисел, составляющих треугольник Паскаля, не удивительна: они возникают в самых естественных задачах алгебры, комбинаторики, теории вероятностей, математического анализа, теории чисел. Этот треугольник можно записать в прямоугольной форме. С 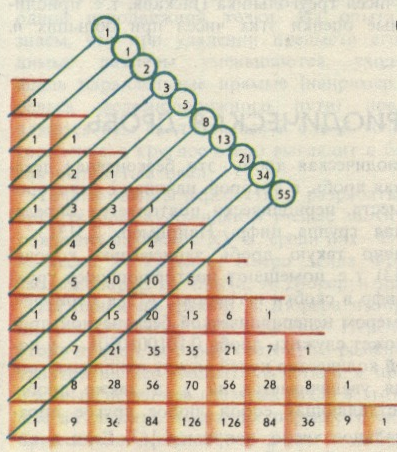 лайд презентации.Суммы чисел по диагоналям равны последовательным числам Фибоначчи. П  риложение 4 |