урок по алгебре в 10 классе. 11 ур. Урок формирования новых знаний Цели урока
 Скачать 181.8 Kb. Скачать 181.8 Kb.
|
|
Тема: Показательные неравенства Тип урока: Урок формирования новых знаний Цели урока: - познакомить обучающихся с показательными неравенствами, формирование знаний об основных методах решения показательных неравенств. – развитие умений сравнивать, выявлять закономерность, обобщать, развитие логики, памяти. – воспитание ответственного отношения к учебному труду, внимательности. Оборудование: проектор, презентация «Показательные неравенства», карточки Этапы урока и их содержание 1. Организационный этап.На уроке будут рассмотрены показательные неравенства, решение которых требует хорошего знания теоретического материала. Данные неравенства ежегодно присутствуют в вариантах ЕГЭ по математике. Вопросы занятия: · рассмотреть основные виды показательных неравенств; · разобрать основные методы решения таких неравенств. Материал урока Давайте определим, какие же неравенства мы будем называть показательными? Определение. Показательными неравенствами называют неравенства вида: 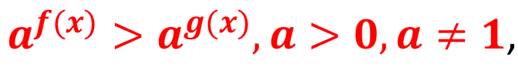 и неравенства, сводящиеся к этому виду. Прежде чем приступить к рассмотрению новой темы, давайте вспомним, какую же функцию мы называем показательной, как выглядит её график и основные свойства показательной функции.  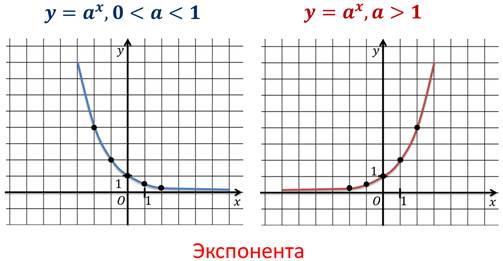 Одно из свойств показательной функции – это свойство монотонности. Если a > 1, то функция возрастающая на всей области определения. Если 0 < a < 1, то функция убывает на всей области определения. То есть выполняются следующие утверждения (поскольку эта тема неразрывно связана с темой «Показательные уравнения», то нумерацию теорем мы продолжим): Теорема 2. Если a > 1, то показательное неравенство: равносильно неравенству Если 0 < a < 1, то показательное неравенство: равносильно неравенству Рассмотрим несколько примеров. Пример.  Пример. 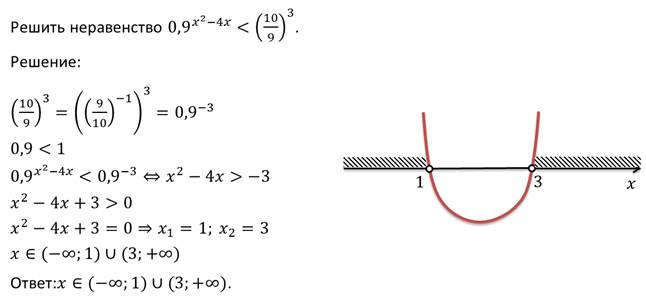 Пример. 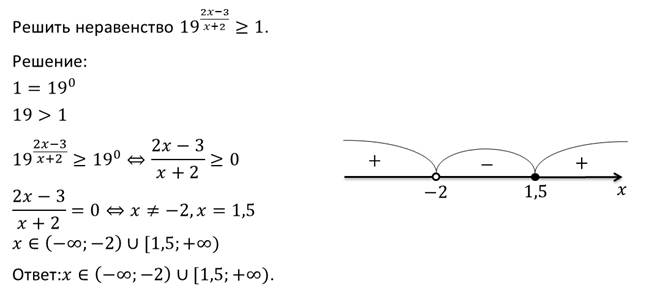 Пример. 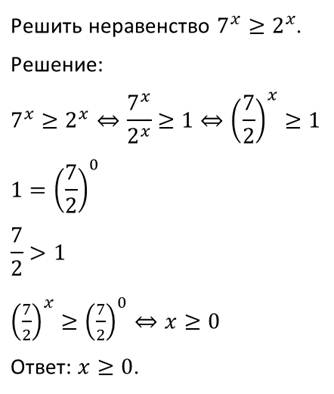 Пример.  Пример. 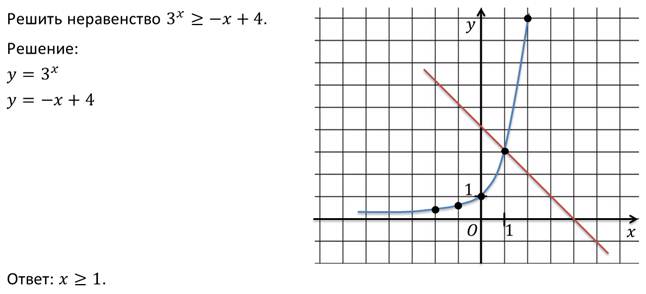 4.Закрепление изученной темы: Решить письменно №3.1, 3.2, 3.4 5.Домашнее задание: п. 3, № 3.3, 3.5 |
