Конспект открытого урока. Конспект урока по математике 5 класс на тему Обыкновенные дроби.. Урок обобщения и систематизации знаний по теме "Обыкновенные дроби"
 Скачать 384.5 Kb. Скачать 384.5 Kb.
|
|
Урок обобщения и систематизации знаний по теме: "Обыкновенные дроби" Цели урока: Образовательные: обобщить и систематизировать изученный материал по данной теме; сформировать навыки работы с обыкновенными дробями; подготовить учащихся к контрольной работе; познакомить учащихся с историческим материалом по изучаемой теме. Развивающие: развивать познавательный интерес, творческие способности, выработать самооценку в выборе пути, критерии оценки своей работы, формировать положительный мотив учения. Воспитательные: воспитывать стремление достигать поставленную цель; чувство ответственности, уверенности в себе, умение работать в коллективе. Оборудование: учебник, сигнальные карточки, путевые листы, Без знания дробей никто не может признаваться знающим математику! Цицерон. Ход урока. 1. Организационный момент.-1 мин. Чтобы спорилось нужное дело, Чтобы в жизни не знать неудач, В путешествие отправимся смело, В мир примеров и разных задач. А девизом нашего урока буду такие слова: Думать - коллективно! Решать - оперативно! Отвечать - доказательно! Бороться - старательно! И открытия нас ждут обязательно! 2. Мотивация урока.-2мин. Математика - наука древняя, интересная и полезная. Слово “математика” пришло к нам из древнегреческого языка. С древнегреческого “мантанейн” означает “учиться”, “приобретать знания”. Математика помогает нам познавать и совершенствовать тот мир, в котором мы живем. Математика поможет нам научиться мыслить яснее и последовательнее. На предыдущих уроках мы с вами убедились, что дроби также как и натуральные числа прочно вошли в нашу повседневную жизнь. И без знаний о дробях нам не обойтись. Не случайно для эпиграфа урока взяты слова Цицерона: «Без знания дробей никто не может признаваться знающим математику!». Поэтому сегодня мы отправимся в удивительное путешествие на единственном в мире «математическом поезде» по удивительной стране «Обыкновенные дроби». Начальником поезда буду я. Каждый ряд – это вагон нашего поезда. А вот и ваши проводницы. Я вместе с ними всегда рада прийти вам на помощь. Для этого достаточно просигналить карточкой – красный цвет.  У каждого из вас есть путевой, в который вы будете заносить результаты путешествия, а в конце урока каждый узнает свою оценку. У каждого из вас есть путевой, в который вы будете заносить результаты путешествия, а в конце урока каждый узнает свою оценку.Прежде всего хотелось бы узнать ваше настроение перед началом путешествия. (Ученики рисуют смайлики в путевом листе).
3. Актуализация опорных знаний. Проверка д/з.- 8 мин. Перед уроком я проверила, как вы собрали багаж к путешествию – оценила ваше домашнее задание. Первая оценка в путевом листе уже выставлена (максимум 5 баллов). Багаж собран. Тогда спешите приобрести посадочные билеты. Игра «Ты – мне, я – тебе» (теоретическая проверка). Вариант 1: Что показывают числитель дроби? (Сколько частей взяли). Какая дробь называется правильной? (Дробь, в которой числитель меньше знаменателя, называют правильной дробью). Какая из двух дробей с одинаковыми знаменателями больше? (Больше та, у которой числитель больше). Как найти дробь от числа? (Число разделить на знаменатель и умножить на числитель дроби). Как складывают дроби с одинаковым знаменателем? (При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же). Вариант 2: Что показывают знаменатель дроби? (На сколько частей разделили целое). Какая дробь называется неправильной? (Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью) Какая из двух дробей с одинаковыми числителями больше? (Больше та, у которой знаменатель меньше). Как найти число по его дроби? (Число разделить на числитель и умножить на знаменатель дроби). Как вычитают дроби с одинаковым знаменателем? (При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же). Билеты приобретены, все заняли свои места в вагонах. Давайте выясним, какой же конечный пункт нашего путешествия. Самостоятельно выберите из предложенных соотношений букву верного: 1 < 0 > Итак, конечный пункт нашего путешествия – успех. (Ученики заносят результаты в оценочный лист. Максимум – 5 баллов). в оценочный лист. Максимум - 5 нт нашего путешествия. множить на зницерона: в). ассм листе)Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата. Желаю всем успеха! Итак, в путь! 4. Путешествие на «математическом поезде». Решение заданий по теме «Обыкновенные дроби». I. Станция «Вычислительная».- 7мин. Поляна «Цветочная». Решение у доски: На лучах солнышка записаны числа, которые надо сложить или вычесть с числом, записанным на солнышке.                Загадка математиков древнего Египта, которые вместо знаков «+» и «-» использовали знаки « а) 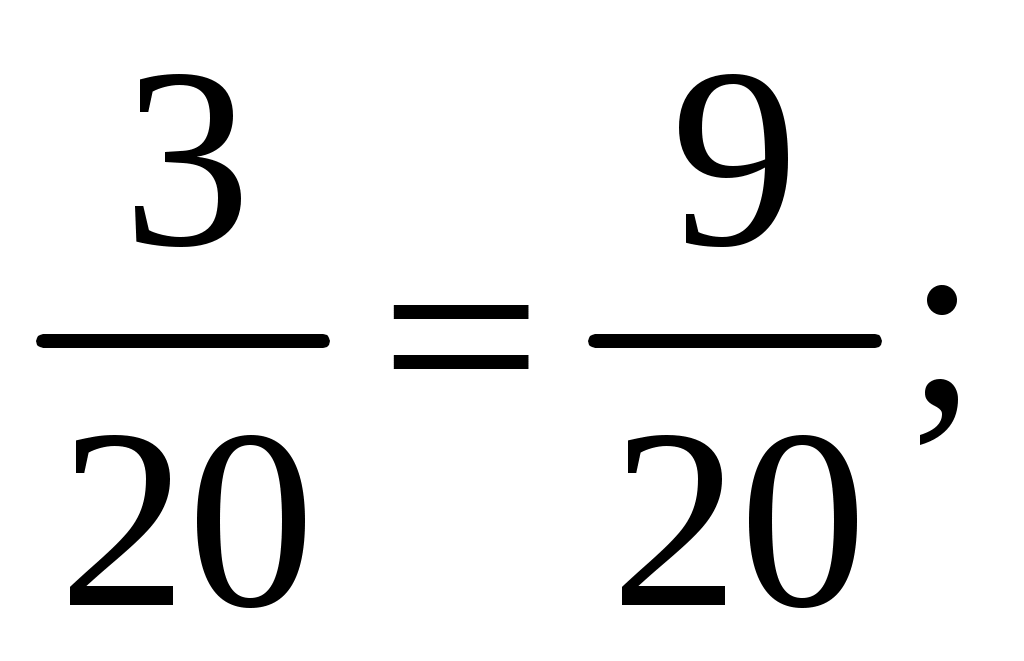 в) в) 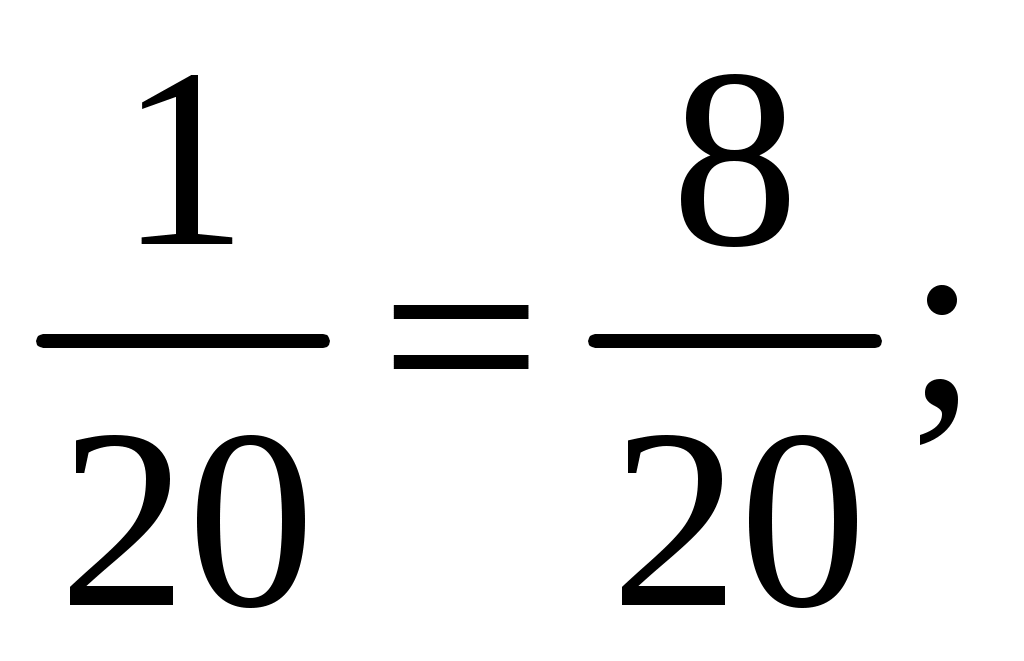 б) 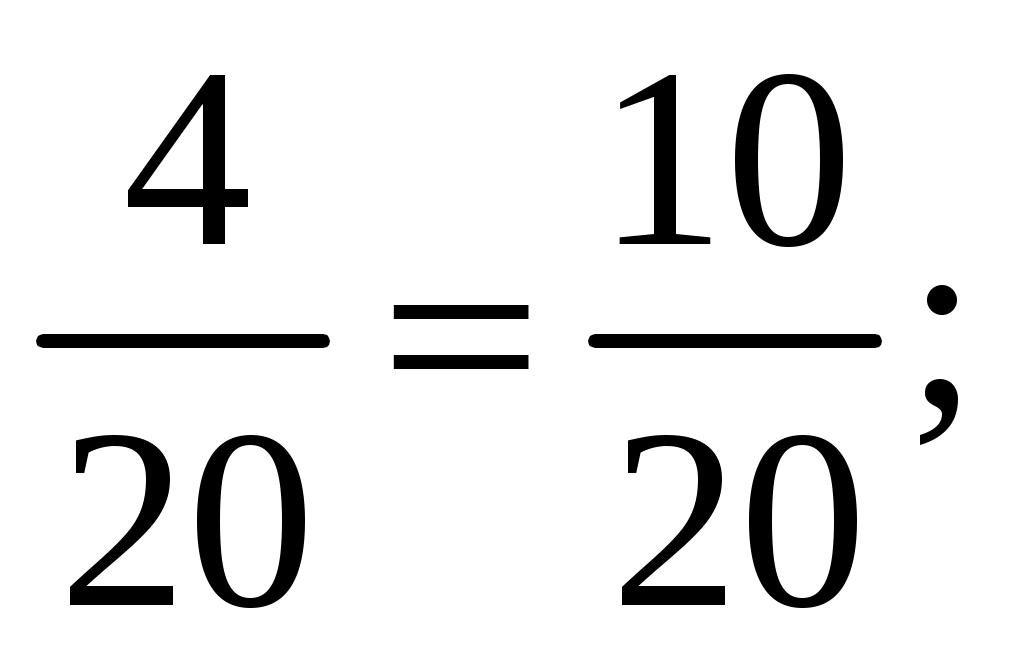 г) г) 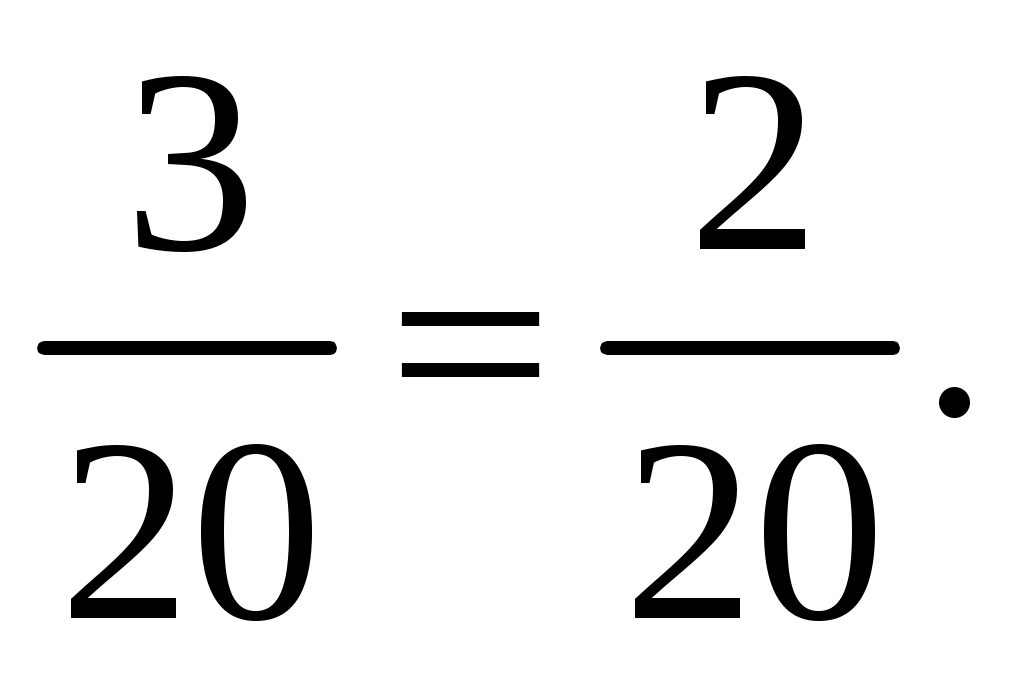 Какое действие обозначено знаком ( Для продолжения путешествия вам необходимо выполнить следующее задание, которое оценивается в 3 балла. Вычислите: Вариант 1: Вариант 2: Затем – взаимопроверка. Заполнение путевых листов. Молодцы. Можно продолжать наше путешествие. II. Волшебные превращения. ТЕСТ. Работа в парах. 1) Смешанное число 13 а) 58; б) 53; в) 17. 2) Из 25 м ткани сшили 8 костюмов. Сколько метров ткани пошло на один костюм? к) 3) Записав, смешанное число 8 л) 4) В записи смешанного числа дробная часть должна быть: в) правильной дробью, с) неправильной дробью, и) любой дробью. 5) Сколько натуральных чисел заключено между числами 8 о) 10; а) 9; т) 12. Проверка. Ответ: браво. Максимум – 5 баллов. III. Физминутка. Станция «Спортивная».- 2мин. Вспомним определения правильных и неправильных дробей. И поиграем в игру «Хлопушка». Я читаю дроби, а если вы услышали среди них неправильную дробь, то ваша задача хлопнуть. Если дробь неправильная – наклоны головы влево, вправо: Потрудились - отдохнём, Встанем, глубоко вздохнём. Руки в стороны, вперёд, Влево, вправо поворот. Три наклона, прямо встать. Руки вниз и вверх поднять. Руки плавно опустили, Всем улыбки подарили. IV. Аукцион от Мистера Х.- 3 мин. Каждый из вас может приобрести товар, решив уравнение: на 3 балла: х+3 на 4 балла: х + 2 на 5 баллов: 11 У доски каждое уравнение решают по 1 ученику. Затем самопроверка. Заполнение путевого листа. V. Станция «Историческая». – 4 мин. Стучат колёса поезда «Вперёд, вперёд, вперёд!» И дроби обыкновенные Изучит наш народ. Откуда появились, И кто придумал их? Мы очень торопились Узнать от сих до сих. Выступление проводниц вагонов: Дроби в Древнем Риме У римлян основной единицей измерения массы,а также и денежной единицей служил «асс». Асс делился на 12 равных частей - унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12… Со временем унции стали применяться для измерения любых величин. Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной. Дроби в Древнем Египте На протяжении многих веков египтяне именовали дроби “ломаным числом”, а первая дробь с которой они познакомились была 1/2. За ней последовали 1/4, 1/8, 1/16, …, затем 1/3, 1/6, …, т.е. самые простые дроби называемые единичными или основными дробями. У них числитель всегда единица. Одним из первых известных упоминаний о египетских дробях является математический папирус Ринда. Египтяне ставили иероглиф 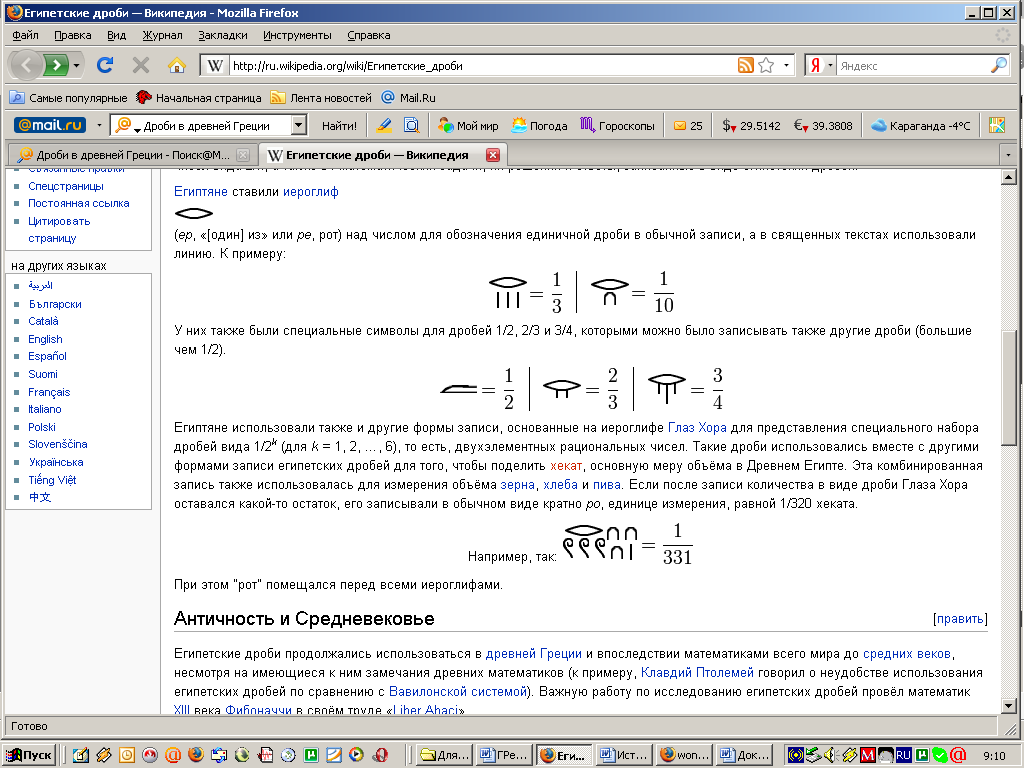 Остальные дроби они записывали в виде суммы долей. Нумерация и дроби в Древней Греции Поскольку греки работали с обыкновенными дробями лишь эпизодически, они использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятиричным дробям. Дроби на Руси В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находим следующие названия дробей на Руси:
Дроби в других государствах древности У индийского математика Брахмагупты мы находим достаточно развитую систему дробей. У него встречаются разные дроби. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим. Арабы первыми начали отделять чертой числитель от знаменателя. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках. Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики. VII. Станция «Угадай-ка». – 5 мин. Станция «Угадай-ка», друзья! Сюда вы прибыли не зря. Головы мы поломайте И задачку разгадайте. 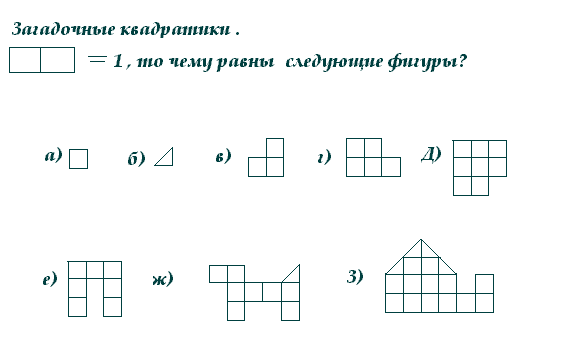 Ответы: За верный ответ-8 баллов. 5. Оценивание. Итоги урока. Рефлексия. Вот и закончилось наше путешествие на математическом поезде по удивительной стране «Обыкновенные дроби». Вы сегодня хорошо потрудились и заработали себе оценки. Подсчитайте сумму полученных баллов и разделите ее на 3. Надеюсь, что каждый из вас достиг желаемого. Упражнение «Микрофон». Вопросы ученикам об уроке: Чем мы занимались на уроке? Чему мы научились на уроке? Что понравилось, не понравилось больше всего? Что хотелось бы еще проводить на следующих уроках? ! - Я работал (а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно. !?- Я работал (а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно. ? - У меня не было желания работать. Сегодня не мой день. Вот закончился урок, Подведём заседания итог, Мы сделали открытие, друзья, Без этого никак нельзя. Формулу площади круга изучили и на практике ее применили. Задачи, находя решенье, развивают мышленье, Память и внимание, закрепляют знания. А теперь, внимание, домашнее задание: Решить №68, 754 (2), 751 (10). Подготовить сообщение «Из истории обыкновенных дробей». Не вызовет оно проблем, Решенье ход известен всем. Урок закончен, друзья, До скорого свидания. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


