|
|
разработка урока. Урока алгебры в 7 классе по теме Формула разности квадратов. Тема Формула разности квадратов. Тип урока Урок открытия новых знаний. Цель урока
Разработка урока математики по ФГОС.
Технологическая карта урока алгебры в 7 классе по теме «Формула разности квадратов».
Тема
|
Формула разности квадратов.
|
Тип урока
|
Урок открытия новых знаний.
|
Цель урока
|
Овладение умением применять формулу разности квадратов при умножении разности двух выражений на их сумму, а также применять эту формулу при разложении многочлена на множители.
|
Задачи
|
Образовательные:
• повторить правило умножения одночленов и многочленов.
• познакомить с формулой разности квадратов и научить применять её при умножении многочленов и
при разложении их на множители
• закрепить полученные знания с помощью упражнений.
Развивающие:
• развитие логического мышления, математической речи, сознательного восприятия материала,
выработка критического мышления, развитие зрительной памяти
• развивать устойчивую мотивацию к процессу обучения.
Воспитательные:
• воспитание культуры общения
• воспитание потребности в самообразовании
• прививать и воспитывать интерес к предмету посредством использования на уроке учебного оборудования
|
УУД
|
Личностные УУД:
- формирование ответственного отношения к учению
- развитие познавательного интереса к предмету
- стремление к совершенствованию речевой культуры
- формирование умения прогнозировать свои действия в ситуации выбора решения задачи
- развитие логического мышления.
Регулятивные УУД:
- умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности
в процессе достижения результата, корректировать свои действия в соответствии с изменившейся ситуацией
- умение оценивать правильность выполнения учебной задачи, собственные возможности её решения
- владение основами самоконтроля, самооценки.
Коммуникативные УУД:
-умение организовывать учебное сотрудничество и совместную деятельность с учителями и со сверстниками
-умение вступать в речевое общение, диалог
-умение включаться в ситуацию выбора методов решения задачи.
Познавательные УУД:
-использовать полученные знания при решении задач
-уметь давать оценку своим действиям, оценивать результат
-уметь выделять главное, обобщать и фиксировать нужную информацию.
|
Планируемые результаты
|
Предметные:
• уметь применять формулу разности квадратов при умножении разности двух выражений на их сумму
• уметь применять формулу разности квадратов при разложении на множители
• применять формулу разности квадратов для нахождения значения выражения.
|
Основные понятия
|
Многочлен, одночлен, умножение многочленов, разложение на множители.
|
Ресурсы:
- основные
- дополнительные
- оборудование
|
Презентация в Power Point c заданиями
Карточки с заданиями для учащихся
Компьютер, проектор
|
Организация пространства
|
Работа фронтальная, самостоятельная, в парах.
|
Образовательные технологии
|
Технология проблемного обучения
ИКТ технологии
Здоровьесберегающие технологии
|
Этапы урока.
I этап. . Мотивация к деятельности.
Содержание
|
Деятельность
учителя
|
Деятельность
ученика
|
Формируемые
УУД
|
Результат взаимодействия
(сотрудничества)
|
Использование ИКТ
(проекции)
|
1. Устная работа.
а)Возвести в степень.
(3a²)² ; (2b³)²; ( x y y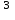 )² )²
б)Выполнить умножение.
2b²c · 3b; 9x · (-4x³) · (-4x³)
3c²(d³ - c² + b)
3c²b(d³ - c² + b)
(a –b)(c + d)
(x + y) (m – n)
в)Сформулировать правила
Умножения одночлена на многочлен и многочлена на многочлен.
2.Выполнить умножение разности двух выражений на их сумму и постараться найти закономерность в ответах.
(a – b) (a + b)
(x – 5) (x + 5)
(x – y) (x + y)
(m+ n) (m – n)
3.(2a - 3) (2a + 3)
(y + 6x) (6x – y)
4.Выполнить умножение:
(с – d) ( c + d)
(a -2) (a +2)
(3 – b) (3 + b)
(x + 4) (x – 4)
|
Приветствие. Проверка готовности.
Включение в деловой режим.
Готовит учащихся к формулированию темы и целей урока.
Предлагает устную работу по повторению.
Организует работу учащихся по ре
Какое из действий умножения самое сложное?
А так как тема нашего сегодняшнего урока «Формула сокращённого умножения», то предлагаю рассмотреть несколько примеров умножения двучленов и постараться увидеть некоторую закономерность, то есть увидеть первую формулу сокращённого умножения.
Цель урока?
Организует работу учащихся по решению проблемной ситуации.
Записывает вывод на доске, даёт образец записи применения формулы на доске(3)
Вопрос:
Как определить, какое выражение будет «первым» при записи разности квадратов?
|
Ученики на примеры 1 отвечают устно, отвечают правила.
Формулируют цель урока с помощью наводящих вопросов учителя:
Вывести формулу сокращённого умножения и научиться применять её при решении примеров.
Примеры под номером2 решают ученики у доски по 2 примера. Вывод:
Произведение разности двух выражений на их сумму равно разности квадратов этих выражений. Записывают вывод в тетрадь:
(a – b) (a + b)= a² - b²
Записывают образец записи примера №3 за учителем.
Ученики делают вывод, что определить «первое» выражение нужно по скобке с разностью.
|
Личностные:
самоопределение
Регулятивные:
целеполагание
Коммуникативные:
планирование учебного сотрудничества с учителем и сверстниками
|
Формулирование темы и целей урока.
|
Слайд 1,2
|
2 этап. Учебно-познавательная деятельность.
5.Выполнить умножение:
1) (4 +5y) (4 – 5y)
2) (7x – 2) (2 +7x)
3) (5a – 8b) (8b + 5a)
4) (c² + d²)(c² - d²)
5) (x - y³) (x - y³) (x + y³) + y³)
6) (100 – 1) (100 + 1)
7) (80 – 3) (80 + 3)
8) 201 · 199
9) Дополнительно.
№ 358(нечётные)
(x - y³) (x - y³) (x + y³) + y³)
(0,2t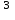 - 0,5 p - 0,5 p )(0,2t )(0,2t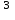 + 0,5 p + 0,5 p ) )
|
Учитель предлагает сформулировать правило умножения разности двух выражений на их сумму.
Указать условие, когда можно применить данную формулу. Как определить, квадрат какого выражения будет стоять на первом месте.
|
Ученики формулируют правило, рассказывают его.
Условие применения формулы: умножаются сумма и разность одних и тех же выражений.
«Первое» выражение определяется по скобке с разностью.
Решают примеры на доске и в тетрадях.
|
Познавательные:
анализ объектов с целью выделения общих признаков,
алгоритмизация
(прикидывание) хода решения
Регулятивные:
оценка и коррекция
Коммуникативные:
планирование учебного сотрудничества со сверстниками и с учителем
|
На доске открывается условие и особенности применения формулы разности квадратов для умножения многочленов.
|
Слайд 3
|
Физкультминутка (учитель проводит)
3 этап. Применение знаний и формирование умений и навыков
.
6. Разложить на множители:
a - b - b
x² - y²
c² - 5²
m²- 25
25 x - 9 №352,353 - 9 №352,353
64y - 36x - 36x (нечётные) (нечётные)
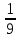 y y - - 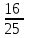 x x
0,25 a² - 0,49b²
|
Учащимся предлагается применить данную формулу ля разложения на множители.
В ходе фронтальной беседы делается вывод.
Вывод :
 раскрытие скобок раскрытие скобок
(a – b) ( a + b) = a - b - b
 разложение на множители разложение на множители
Т.е. если применять формулу слева направо(выполнять умножение) – это раскрытие скобок,
А если справа налево, то это разложение на множители.
|
Ученики вместе с учителем делают данный вывод и делают записи в тетради.
Раскладывают на множители.
В ходе решения примеров и фронтальной беседы с учителем учащиеся отвечают на вопрос учителя, что нужно сделать с выражениями, чтобы применить формулу разности квадратов для разложения на множители.
Представить их в виде квадратов, т.е. ( )²-( )²
Решают примеры у доски, класс корректирует работу отвечающих у доски, задают возникающие вопросы.
|
Познавательные:
-использование символов и схем для разложения на множители
- алгоритмизация
(прикидывание) хода решения
Коммуникативные:
- совместная познавательная деятельность с учителем и одноклассниками,
- развитие устной и письменной речи,
- формирование умения вступать в диалог.
|
На доске выводится формула разности квадратов и возможность её использования: слева –направо и
справа – налево.
|
Слайд4,5
|
4 этап. Контроль знаний.
Самостоятельная работа.
I вариант
II вариант
|
Предлагает выполнить самостоятельную работу по карточкам с последующей проверкой в классе.
|
Ученики выполняют работу самостоятельно.
Проверяют работу у соседа по парте.
Выставляют оценку в соответствии с критериями.
|
Регулятивные:
Контроль, оценка, коррекция.
Личностные:
смыслообразование
|
Анализ работы и её результативность.
|
Слайд 6,7
(проверка)
|
5 этап. Рефлексия.
Подведение итогов
|
Учитель задаёт домашнее задание с комментарием.
Предлагает заполнить анкету (лист самооценки)
|
Ученики оценивают результаты своей работы, задают вопросы, обсуждают возможные свои промахи.
Ученики заполняют анкету (лист самооценки)
|
Личностные:
понимание причин затруднений.
|
Подведение итогов урока, информация о домашнем задании.
|
|
Самостоятельная работа
по теме «Формула разности квадратов»
I вариант.
|
II вариант.
|
Выполнить умножение
с использованием формулы
(a – b) (a + b) = a - b - b
1) (a - 2) (a + 2)
2) (3b – 1) (3b +1)
3) (a + 2b) (a – 2b)
4) (4a – 5b) (4a + 5b)
5)(2a² + 3b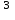 ) (3b ) (3b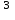 - 2a²) - 2a²)
|
Разложить на множители с использованием формулы
a - b - b = (a – b) (a + b) = (a – b) (a + b)
4x - 9 - 9
m - a - a
x - 9 y - 9 y
25 - 36 a
x²y² - 1
|
Выполнить умножение
с использованием формулы
(a – b) (a + b) = a - b - b
1) ( b -3) (b + 3)
2) (2c – 1) (2c +1)
3) (x + 3y) (x – 3y)
4) (2a – 3b) (2a + 3b)
5)(3x² + 2y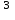 ) (2y ) (2y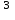 - 3x²) - 3x²)
|
Разложить на множители с использованием формулы
a - b - b = (a – b) (a + b) = (a – b) (a + b)
9y² - 16
c² - d²
a² - 4 b²
49 – 25x²
a²b² - 9
|
Дополнительно: Разложить на множители:
1) 144a c c x x - 225; 2) a - 225; 2) a - 9; 3) (2a + 7b) - 9; 3) (2a + 7b) - (3a – 5b) - (3a – 5b)
|
Дополнительно: Разложить на множители:
1)100a b b c c - 121; 2) x - 121; 2) x - 4 ; 3) (3x + 1) - 4 ; 3) (3x + 1) - (4x + 3) - (4x + 3) 
|
Анкета.
На уроке я работал (а)
|
активно / пассивно
|
Своей работой на уроке я
|
доволен / не доволен
|
Урок мне показался
|
коротким / длинным
|
За урок я
|
не устал / устал
|
Моё настроение стало
|
стало лучше / стало хуже
|
Материал урока мне был
|
понятен / не понятен
полезен / бесполезен
интересен / скучен
|
Домашнее задание мне кажется
|
лёгким / трудным
интересным / неинтересным
|
Ссылки на источники:
Новая дидактика современного урока в условиях введения ФГОС ООО. Издательство КАРО,СПб, 2013. Крылова О.Н.,
Муштавинская И.В.
Учебник «Алгебра 7 класс. Москва « Просвещение» 2012 год. Колягин Ю.М., Ткачёва М.В.
Дидактические материалы. Алгебра 7 класс. Москва « Просвещение» 2011 год, ЗвавичЛ.И.
Дидактические материалы. Алгебра 7 класс. Москва « Просвещение» 2015 год. Ткачёва М.В.
Системно-деятельный подход в реализации стандартов нового поколения» Фисенко Т.
Приложение
|
|
|
 Скачать 0.5 Mb.
Скачать 0.5 Mb.
 y
y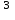 )²
)² - y³) (x
- y³) (x - b
- b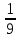 y
y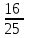 x
x раскрытие скобок
раскрытие скобок - 9; 3) (2a + 7b)
- 9; 3) (2a + 7b)






