разработка. Тема урока. Урока Прямоугольная система координат. Тип урока открытие новых знаний. Основные цели
 Скачать 45.17 Kb.
|
|
Тема урока «Прямоугольная система координат». Тип урока: «открытие» новых знаний. Основные цели: сформировать понятие координатной плоскости, способность к определению координат точек и построению точек по их координатам; повторить и закрепить: действия с рациональными числами, понятие модуля числа, решение уравнений и неравенств с модулем. 1. Самоопределение к деятельности. - Здравствуйте, ребята! – Какое задание дома не соответствовало теме, которую мы изучали последние уроки? (Построение многоугольника по координатам его вершин). – Что вам необходимо было вспомнить при выполнении этого задания? (Правило построения точек на координатном угле). – В жизни мы сталкиваемся с понятиями координаты точек, определение координат? (Да, координаты местонахождения, какого то человека или объекта, это значит некоторые данные, по которым можно было бы этого человека или объект найти). – Важно уметь понимать, как задать или как заданы координаты? (От этого зависит найдём мы этот объект или нет) – Вы заметили, какую-нибудь особенность в координатах точек, в домашнем задании? (Среди координат не было положительных чисел). - Сегодня мы продолжим изучение правила построения точек с координатами, выраженными рациональными числами. 2. Актуализация знаний и фиксация затруднения в деятельности. 1. Вычислите:
– Назовите полученные результаты в порядке убывания. Какую закономерность вы заметили? (- 3; - 5; - 7; - 9; каждое следующее число меньше предыдущего на 2). – Продолжите ряд на три числа вперед. (- 3; - 5; - 7; - 9; - 11; - 13; - 15)
2. Назовите модуль координат точек, отмеченных на координатной прямой: 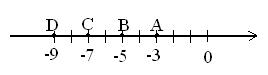 (9; 7; 5; 3; 0). 3. Назовите координаты точек A, K, Q на координатном угле: 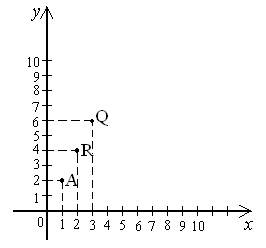 (А (1; 2); R (2; 4); Q (3; 6)) Индивидуальное задание: – Нарисуйте на середине листа координатный угол и постройте точки с координатами: А (- 1; 2); R (- 2; 4); Q (- 3; - 6). 3. Выявление причин затруднения и постановка цели деятельности. - В чем возникло затруднение? (В координатном угле построить эти точки нельзя, т.к. ни на оси абсцисс, ни на оси ординат нет точек, соответствующих отрицательным числам.) - Какая задача встала перед нами? (Расширить координатный угол, чтобы можно было отмечать точки с любыми координатами). - Сформулируйте тему урока. (Правило построения точек с рациональными координатами) - Запишите тему в тетрадях. 4. Построение проекта выхода из затруднения. – Какие есть предложения? Если предложений не будет, то спросить ребят, что мы сделали, когда у нас встала необходимость отметить на координатном луче точку с отрицательной координатой. (Координатный луч заменили координатной прямой). – Что надо сделать с координатными лучами в координатном угле? (Заменить их координатными прямыми). – Вспомните определение координатного угла. (Координатный угол – это два взаимно перпендикулярных луча: их общее начало – начало отсчёта, выбран единичный отрезок, указано направление стрелочками, обозначены лучи (луч ОХ – ось абсцисс, луч ОY – ось ординат). Определение на доске – Что в этом определении надо изменить? (Слово лучи заменить на прямые). – Прочтите, что получится. (Учащиеся читают постепенно заменяя некоторые слова на новые: вместо слова лучи на доске появляется слово прямые, их общее начало на их точка пересечения.) – Что ещё осталось заменить? (Координатный угол, потому, что получилось четыре угла). – Чем можно заменить координатный угол? (Учащиеся предлагают свои варианты, в итоге обсуждения появляется название координатная плоскость). – Нарисуйте в соответствии определению координатную плоскость. В тетрадях выполняют задание самостоятельно.  y 1  0 1 x – Сколько углов образовалось при построении координатной плоскости? (Четыре координатных угла). – В математике принято обозначать эти углы римскими цифрами. Как вы думаете, какой первый координатный угол? (Наверно тот, из которого получилась плоскость). – Верно, а дальше нумерация производится против часовой стрелки. – Пронумеруйте координатные углы или их ещё называют координатные четверти. Учащиеся выполняют задание самостоятельно, затем проверяют подоске. yII I 1 0 1 x III IV – Что надо помнить, когда строим точки по координатам или определяем координаты по точке на плоскости? (Что первая координата всегда берётся на оси абсцисс, а вторая на оси ординат). – Запишите в общем виде координату любой точке. А (x; y) – Теперь вы можете выполнить задание, которое вам было предложено? (Да). Учащиеся выполняют задание в тетрадях, три ученика у доски (по одному строят по одной точке) – Составьте алгоритм построения точек на координатной плоскости. Алгоритм построения точек в координатной плоскости. Найти на оси абсцисс число соответствующее первой координате (провести через неё пунктирную прямую). Найти на оси ординат число соответствующее второй координате (провести через неё пунктирную прямую). Отметить точку пересечения пунктирных прямых, обозначить заглавной буквой латинского алфавита. 5. Первичное закрепление во внешней речи. № 171 (первые две точки строят учащиеся у доски, работая по алгоритму, построение двух других точек проговаривают в парах). – Что надо уметь, чтобы ответить на поставленный вопрос? (Как определить координаты построенной точки). – Составьте алгоритм определение координат токи в координатной плоскости. Алгоритм определения координат точки в координатной плоскости. Провести пунктирные прямые из точки на оси координат. Указать числа, соответствующие точкам пересечения пунктирных прямых с осями координат. Записать точку и в скобках её координаты: первая по оси абсцисс, вторая по оси ординат. – Выполните задание до конца. (Один ученик выполняет задание, опираясь на алгоритм). 6. Самостоятельная работа с самопроверкой по эталону. № 176 (а) На доске дан эталон выполнения задания по алгоритму. После проверки и анализа результатов отвечаем на два дополнительных вопроса, предложенных в задании. 7. Включение в систему знаний и повторение № 176 (б, в) № 185; 186; 187. 8. Рефлексия деятельности. - Что нового вы узнали на уроке? - Что использовали для «открытия» нового знания? - Мы достигли поставленной цели? - Как вы оцените свою работу на уроке? Домашнее задание: П.3.4.1, № 196, № 197; 204, принести миллиметровую бумагу |
; 
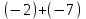
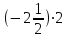
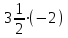
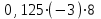
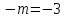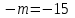. (3; 15).