доклад. вадим. Условия равновесия систем пар сил
 Скачать 499.12 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ ТАТАРСТАН ГАПОУ «Лениногорский нефтяной техникум» Реферат На тему: «Условия равновесия систем пар сил» По дисциплине «Техническая механика» Студента (ки): Новикого Вадима Сергеевича Группы: Б-20 Преподаватель: Галимова А.И. 2021-2022 учебный год Ведение Пара сил. Теорема о сумме моментов пары сил. Теорема об эквивалентности пар сил. Теорема о переносе пары сил в параллельную плоскость. Теорема о сложении пар сил. Условия равновесия пар сил. эквивалентность сила равновесие плоскость Условия равновесия тел Статикой называется раздел механики, изучающий условия равновесия тел. Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс. Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.  или  
На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил  и  не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы. Произведение модуля силы  на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:  В Международной системе единиц (СИ) моменты сил измеряются в Ньютон—метрах (Н∙м).
В общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов сил.
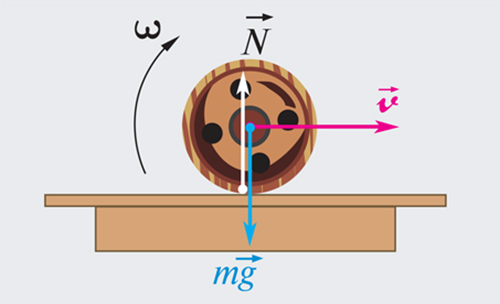
Катящееся по горизонтальной поверхности колесо – пример безразличного равновесия (рис. 1.14.3). Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Наряду с безразличным равновесием в механике различают состояния устойчивого и неустойчивого равновесия. Состояние равновесия называется устойчивым, если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние. При малом отклонении тела из состояния неустойчивого равновесия возникают силы или моменты сил, стремящиеся удалить тело от положения равновесия. Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия. Шар, находящийся в верхней точке сферического выступа, – пример неустойчивого равновесия. Наконец, шар на дне сферического углубления находится в состоянии устойчивого равновесия (рис. 1.14.4).
Для тела, имеющего неподвижную ось вращения, возможны все три вида равновесия. Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым. Если же центр масс расположен выше оси – состояние равновесия неустойчиво (рис. 1.14.5).
Особым случаем является равновесие тела на опоре. В этом случае упругая сила опоры приложена не к одной точке, а распределена по основанию тела. Тело находится в равновесии, если вертикальная линия, проведенная через центр масс тела, проходит через площадь опоры, т. е. внутри контура, образованного линиями, соединяющими точки опоры. Если же эта линия не пересекает площадь опоры, то тело опрокидывается. Интересным примером равновесия тела на опоре является падающая башня в итальянском городе Пиза (рис. 1.14.6), которую по преданию использовал Галилей при изучении законов свободного падения тел. Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. Вершина башни отклонена от вертикали на 4,5 м. Вертикальная линия, проведенная через центр масс башни, пересекает основание приблизительно в 2,3 м от его центра. Таким образом, башня находится в состоянии равновесия. Равновесие нарушится и башня упадет, когда отклонение ее вершины от вертикали достигнет 14 м. По-видимому, это произойдет очень нескоро.
Заключение Таким образом, изучив данную тему. Мы поняли, что для общего случая произвольную пространственную систему сил, для них получены условия равновесия в виде соотношений. Узнали формлы и дествия сил на объекты. Список литературы wiki/%CC%EE%EC%E5%ED%F2 %F1%E8%EB%FB› fizika_i_energetika/m ment_silya_para_sil_ _ee_svojst a.html |
– сила тяжести; 
– упругая сила оси; d – плечо