РГР ТУС. Устрій судна та морехідні якості

• Название: Устрій судна та морехідні якості
• Дата: 28.10.2018
• Размер: 0.73 Mb.
• Имя файла: РГР ТУС.docx
• Тип: Документы; #54812

Міністерство освіти і науки україни

Національний університет «Одеська морська Академія»

Дунайський інститут

Розрахункова графічна робота

«Устрій судна та морехідні якості»


Виконав: ,

3СМ, шифр:


Ізмаїл – 2018

1. Плавучесть.
Первое условие равновесия судна на плаву: масса судна должна равняться массе вытесненной им воды:

D =γ V,

Где D- массовое водоизмещение судна, т;

V- объёмное водоизмещение, м³;

γ- плотность забортной воды, т/ м³;

Второе условие равновесия: ЦТ и ЦВ судна должны лежать на одной вертикали. При отсутствии дифферента:

xg =xc
здесь xg - отстояние от миделя ЦТ судна G (абсцисса ), м;

xc - отстояние от миделя ЦВ судна C (абсцисса), м;
Грузовой размер или кривую водоизмещения, строят для того, чтобы находить водоизмещение судна при различных осадках, не прибегая к вычислениям.

Кривые V и D , так же как и ряд других величин рассчитываются по теоретическому чертежу при проектировании судна и изображаются в виде кривых в функции осадки.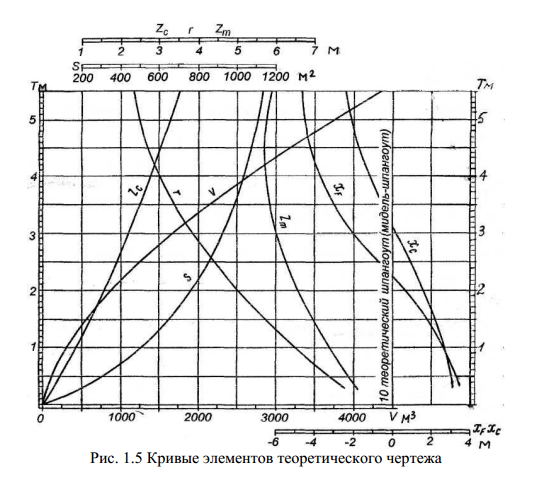



В судовых условиях для определения водоизмещения по заданной осадке и решения обратной задачи пользуются грузовой шкалой.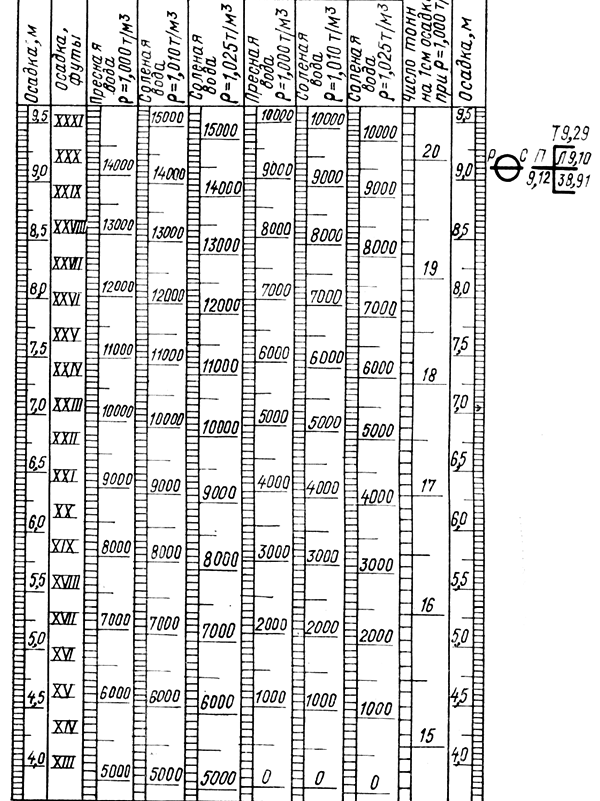



Некоторые приближенные формулы для расчетов:

-число тонн на 1 см осадки q = γS/100, где q - число тонн, которое нужно принять или снять, чтобы изменить осадку на 1 см, т/см; S- площадь ватерлинии, определяется по кривым элементам для заданной осадки.

- изменение осадки при приёме/снятии груза Δd = M/ γS = M/100q, где M - масса принятого груза, при снятии груза перед M и Δd ставится знак минус. Формула приближенная, она будет точной если в пределах изменения осадки борта судна прямостенны.

-изменение осадки судна при изменении солености воды выражается формулой

Δd = V/ S·( γ1 - γ2)/ γ2, где объёмное водоизмещение судна до перехода в воду другой солености, , м³; γ1 и γ2 –плотность воды, из которой и в которую переходит судно;

Так как изменение осадки при перемене солености невелико формулу можно считать точной.

При построении грузового размера и грузовой шкалы предполагается, что судно плавает в воде определенной солености (обычно γ = 1,025 т/ м³), не имеет дифферента и не подвержено продольному изгибу. В действительности плотность воды может быть другой, а суда большой длины могут иметь существенный прогиб или перегиб. Кроме того, при наличии дифферента пользуются средней осадкой, определяемой по маркам углублений, но они обычно находятся на не на одинаковых расстояниях от миделя, что ведет к погрешности в определении средней осадки.

Все это приводит к погрешностям при определении водоизмещения, которыми из-за их небольшой величины (4-5%) можно было- бы не учитывать, однако при перевозке грузов приём-сдача которых в портах производится без взвешивания- по осадке, эти погрешности необходимо принимать во внимание.

-поправка на плотность воды: M1 =(γ – γ0)/ γ·Dср

где: γ - плотность воды, в которой находится судно, т/ м³;

γ0 - расчетная плотность воды, т/ м³;

Dср – водоизмещение судна, найденное по средней осадке, т;

-поправка на расположение марок углублений: M2 = -50 q·d/L·(Xн +Xк)

где: d- дифферент (на корму отрицательный), м;

L- длина судна между перпендикулярами, м;

Xн иXк- расстояние от миделя марок углублений (в корму отрицательна), м;

-поправка на дифферент: M3 =100· q ·Xf· d/L

где: Xf - абсцисса ЦТ площади ватерлинии при данной средней осадке и положении судна на ровный киль (в корму отрицательна), м;

-поправка на изгиб корпуса: M4 = Kqf

где: К – коэффициент;

f –стрелка прогиба корпуса, см;

Для грубых подсчетов К = 0,75. Более точное значение: К = 1-0,334α

Стрелку прогиба находят как разность осадки судна на миделе и средней осадки.

Поправку M4 прибавляют к водоизмещению, найденному по средней осадке, когда осадка на миделе больше средней (прогиб судна), и вычитают в противном случае.

Все приведенные выше поправки измеряются в тоннах.


2. Поперечная остойчивость и малые углы крена.

Малым углом крена считают угол до 10 градусов. В отличии от больших углов крена при малых углах можно пользоваться метацентрическими формулами остойчивости, которые при больших углах дают большую погрешность и они заменяются различными диаграммами.

Величиной, характеризующей начальную поперечную остойчивость, является поперечная метацентрическая высота h.

Метацентрическая высота является универсальной характеристикой остойчивости судна, так как косвенно она характеризует остойчивость и на больших углах крена.

Основой для теоретических положений и практических их применений является метацентрическая формула остойчивости:
Mв = Dhθ = Dhsinθ,

где Mв –восстанавливающий момент, тм;

D - водоизмещение, т;

h -метацентрическая высота, м;

θ -угол крена (в первом случае- радианы, во втором –градусы);

Формула выведена для бесконечно малых углов наклонения и применима для углов до 10 градусов.

Для того чтобы судно в наклонном положении было в равновесии, необходимо равенство кренящего и восстанавливающего моментов:

Mкр = Mв

Кренящий момент при переносе груза поперек судна равен

Mкр =ml cosθ

где m -масса груза, т;

l - расстояние, на которое груз перенесен, м;

При малых углах крена обычно принимается cosθ=1.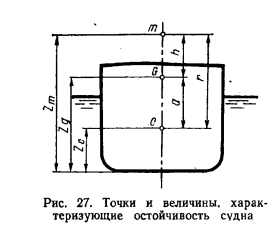



Метацентрическая высота это возвышение метацентра над ЦТ судна. Если ЦТ поднимается выше метацентра, высота становится отрицательной:
h = r + zc - zg; h = zm - zg; h = r – α
где r -метацентрический радиус, м;

zc -отстояние от основной плоскости (аппликата) центра величины C , м;

zg -апликата ЦТ G, м;

zm -апликата поперечного метацентра m, м;

α-возвышение ЦТ над ЦВ, м;
Метацентрический радиус равен
r =Ix/V

где Ix - момент инерции площади ватерлинии относительно продольной оси х, лежащей в её плоскости;

V - объёмное водоизмещение судна по данную ватерлинию, м³;

Величины r, zc и zm вычисляются заранее в конструкторском бюро в зависимости от осадок судна и вычерчивают на метацентрической диаграмме. Она входит в состав кривых элементов теоретического чертежа.
Аппликата ЦТ судна zg определяется распределением грузов на судне.
Момент инерции прямоугольника относительно оси, проходящей через его ЦТ(собственный момент инерции) вычисляют по формуле:
I = lb³/12
где l - сторона прямоугольника, параллельная оси, относительно которой находят момент;

b - сторона, перпендикулярная этой оси.
Изменение метацентрической высоты от перемещения груза в вертикальном направлении:

Δh =m/D(z0-z1) = ml/D
где z0 и z1 отстояние от основной плоскости ЦТ первоначальное и после его перемещения, м;

l - Расстояние, на которое груз перемещается по вертикали (считается положительным, когда груз опускается), м;

Формула действительна как для малого, так и для большого груза.

Центр тяжести подвешенного груза следует считать расположенным в точке подвеса. В момент отделения груза от места, где он лежал, метацентрическая высота сразу уменьшается и дальнейший подъём его на остойчивость уже не влияет. В данном случае z1 есть отстояние точки подвеса (блока шкентеля) от основной плоскости, а l - расстояние между лежащим грузом и блоком (считается отрицательным).


Жидкий груз, имеющий свободную поверхность, отрицательно влияет на остойчивость судна и определяется по формуле:
Δh = -Ix·γ/D
где Ix –момент инерции площади свободной поверхности жидкости относительно оси, проходящей через ЦТ площади;

Изменение метацентрической высоты вследствие приёма груза определяется по приближенной формуле:

Δh = m/(D+m)(d+m/200q-zp – h)

где zp - отстояние (аппликата) ЦТ груза от основной плоскости, м;

Принимаемый груз считается положительным, а снимаемый отрицательным.

D, d, h имеют значения до приёма/снятия груза.

Массу балласта, необходимого для придания судну заданной остойчивости, определяют по формуле:

M = D· Δh/(1.01d- zp –h- Δh)
Остойчивость на больших углах крена
Большими углами крен считаются углы более 10 градусов. Пользование формулами для начальной остойчивости при больших углах крена ведет к значительным погрешностям т.к. в этих случаях площадь действующей ватерлинии и её момент инерции изменяется весьма существенно. При малых углах крена этого не происходит и величина метацентрического радиуса практически не изменяется.

В виде формул эту зависимость выразить слишком сложно, поэтому она изображается графически в виде диаграммы статической остойчивости (ДСО).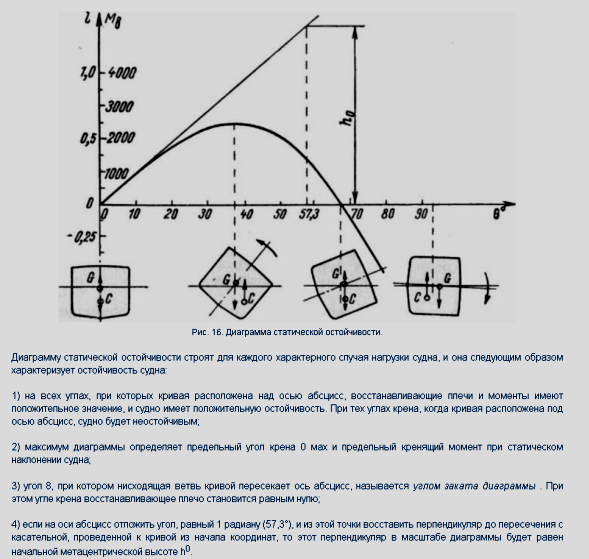



На горизонтальной оси ДСО наносят масштаб углов крена, а на вертикальной- моментов или плеч моментов.

Плечо восстанавливающего момента определяется длиной перпендикуляра, опущенного из ЦТ судна, находящегося в прямом положении на линию действия силы поддержания при наличии крена:

l = lф – zg *sinθ

lф - плечо остойчивости формы, м;

θ - угол крена, при котором определяется плечо остойчивости, град;

zg - возвышение ЦТ над ЦВ в прямом положении судна, м;

Величина кренящего момента, возникающего от переноса груза поперек судна, зависит от угла крена и выражается формулой:

Mкр = my cosθ

m - масса переносимого груза, т;

y -расстояние, на которое перемещается груз, м;

Плечи статической остойчивости при изменении положения ЦТ судна вычисляются по формуле:

l1 = l - (zg1-zg)sinθ

l - плечо статической остойчивости при первоначальном положении ЦТ судна, м;

zg1 и zg - первоначальная и измененная апликата ЦТ судна, м;

Для построения ДСО, соответствующей заданной нагрузке находятся плечи восстанавливающих моментов при различных углах крена. Более удобной для пользования является универсальная ДСО.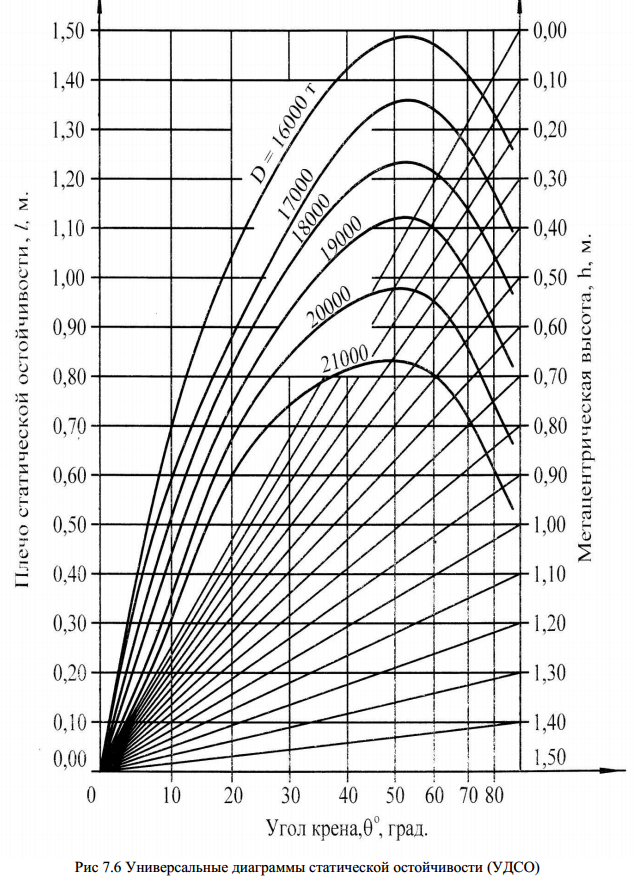


3. Определить какие междудонные отсеки нужно заполнить водяным балластом для увеличения остойчивости судна: осадка судна d=7.1м; водоизмещение D=12000т; метацентрическая высота h=0.1м; Объёмы отсеков, куб. М: № 1-1х142; № 2-2х170; № 3-2х125; № 4-2х70; №5-2х150; № 6-1х116. Метацентрическая высота должна быть не менее 0.5 метра.
Массу балласта, необходимого для придания судну заданной остойчивости, определяют по формуле:

M = D· Δh/(1.01d- zp –h- Δh)
M=(12000*0.4)/(1.01*7.1-0.6-0.1-0.4)=4800/6=800т
Объём который будет занимать вода вычеслим по формуле:
V = M/P
V=800/1.025=800 м³
Варианты заполнения трюмов будут:

№1, №2(2),№5(2)
№1,№2(2),№3(2),№4(1)
№2(2),№4(1),№5(2),№6
№1,№3(2),№5(2),№6