Лабораторная работа 2 (1). Устройство рентгеновского дифрактометра и основы рентгеноструктурного анализа поликристаллических материалов
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
10−3 нм). Оно возникает в результате замедления заряженных частиц (при бомбардировке вещества быстро летящими электронами).
10−2 Å (от 10 эВ до нескольких МэВ), что соответствует длинам волн от |
ВВЕДЕНИЕ 3
1 Историческая справка 5
2 Происхождение рентгеновского излучения 6
2.1 Источники рентгеновского излучения 6
2.2 Возникновение рентгеновского излучения 7
3 Условие возникновения дифракции в кристалле, закон Брэгга-Вульфа 9
3.1 Дифракция 9
3.2 Закон Брэгга-Вульфа 13
4.1 Решётка Браве 18
4.2 Индексы Миллера 20
4.2.1 Индексы узла. 20
4.2.2 Индексы плоскости. 21
4.2.3 Индексы направления. 21
4.3 Сингонии 22
5.Рентгенографический метод контроля в металлографии 25
5.1 Преимущества рентгенографического контроля 26
Заключение 28
Различают два типа рентгеновского излучения - тормозное (непрерывный спектр) и характеристическое (дискретный спектр). Наличие непрерывного тормозного излучения является следствием неупругого торможения ускоренных электронов мишенью.
Одним из методов применения рентгеновского излучения является рентгеноструктурный анализ (рентгенодифракционный анализ) — один из дифракционных методов исследования структуры вещества. В основе данного метода лежит явление дифракции рентгеновских лучей на трёхмерной кристаллической решётке.
Рентгеноструктурный анализ во многих отраслях, например, в науке, медицине, производстве и т.д. Методами рентгеноструктурного анализа изучают металлы, сплавы, неорганические и органические соединения, аморфные материалы, жидкости, газы, молекулы белков, нуклеиновых кислот и т.д.
Рентгеноструктурный анализ позволяет определить координаты атомов в пространстве, степень совершенства кристаллов и наличие в них зональных напряжений, размер мозаичных блоков в монокристаллах, тип твердых растворов, степень их упорядоченности и границы растворимости, размер и ориентировку частиц в дисперсных системах, текстуру веществ и состояние поверхностных слоев различных материалов, плотность, коэффициент термического расширения, толщину листовых материалов и покрытий, внутренние микродефекты в изделиях (дефектоскопия), поведение веществ при низких и высоких температурах и давлениях и т. д.
1 Историческая справка
Рентгеновское излучение было открыто Вильгельмом Конрадом Рентгеном 8 ноября 1895 г. Открытие Рентген совершил неожиданно для себя: поздним вечером, уходя из лаборатории, учёный погасил свет в комнате и заметил в темноте зеленоватое свечение, флюоресценцию, исходившую от экрана, покрытого кристаллами платино-синеродистого бария.
Как оказалось, кристаллы отреагировали на воздействие на них расположенной неподалёку электровакуумной трубки, которая в тот момент находилась под высоким напряжением. При отключении тока свечение экрана прекращалось, а при повторном включении снова возобновлялось.
Трубка была обёрнута в чёрную светонепроницаемую бумагу, поэтому Рентген предположил, что при прохождении через неё электрического тока она испускает какие-то невидимые лучи, способные проникать через непрозрачные среды и возбуждать кристаллы бария. Эти неизвестные лучи Рентген назвал X-лучами.
Через 50 дней учёный представил председателю Вюрцбургского физико-медицинского общества рукопись из 17 страниц, содержащую описание открытых им лучей. Этот день, 28 декабря 1895 г., вошёл в историю как официальная дата открытия рентгеновских лучей.
Вместе с рукописью учёный представил также первую рентгенограмму, сделанную ранее, 22 декабря, на которой была запечатлена рука его жены - Берты Рентген.
Но ещё за 8 лет до этого — в 1887 году Никола Тесла в дневниковых записях зафиксировал результаты исследования рентгеновских лучей и испускаемое ими тормозное излучение, однако ни Тесла, ни его окружение не придали серьёзное значение этим наблюдениям. Кроме этого, уже тогда Тесла предположил опасность длительного воздействия рентгеновских лучей на человеческий организм.
2 Происхождение рентгеновского излучения
2.1 Источники рентгеновского излучения
Естественными источниками рентгеновского излучения являются некоторые радиоактивные изотопы (например, 55Fe). Искусственными источниками мощного рентгеновского излучения являются рентгеновские трубки (рисунок 1).
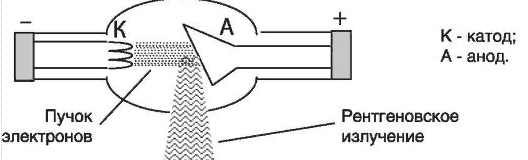
Рисунок 1 – Устройство рентгеновской трубки
Рентгеновская трубка представляет собой вакуумированную стеклянную колбу с двумя электродами: анодом А и катодом К, между которыми создается высокое напряжение U (1-500 кВ). Катод представляет собой спираль, нагреваемую электрическим током. Электроны, испущенные нагретым катодом (термоэлектронная эмиссия), разгоняются электрическим полем до больших скоростей (для этого и нужно высокое напряжение) и попадают на анод трубки. При взаимодействии этих электронов с веществом анода возникают два вида рентгеновского излучения: тормозное и характеристическое.
Рабочая поверхность анода расположена под некоторым углом к направлению электронного пучка, для того чтобы создать требуемое направление рентгеновских лучей.
В рентгеновское излучение превращается примерно 1 % кинетической энергии электронов. Остальная часть энергии выделяется в виде тепла. Поэтому рабочая поверхность анода выполняется из тугоплавкого материала
2.2 Возникновение рентгеновского излучения
Рентгеновское излучение возникает в результате замедления заряженных частиц (при бомбардировке вещества быстро летящими электронами).
Различают два типа рентгеновского излучения - тормозное (непрерывный спектр) и характеристическое (дискретный спектр). Наличие непрерывного тормозного излучения является следствием неупругого торможения ускоренных электронов мишенью.
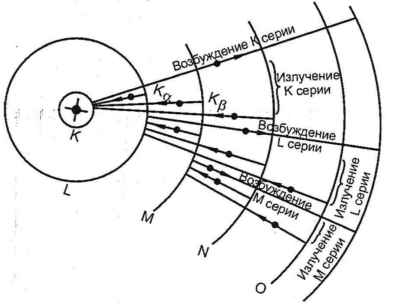
Характеристический, или линейчатый спектр возникает при поглощении атомом порции энергии достаточной для возбуждения одного из внутренних электронов. Атом возвращается в невозбужденное состояние путем самопроизвольного заполнения вакансии электроном с других оболочек. Избыток энергии, равный разности энергий электрона на этих уровнях, выделяется в виде кванта рентгеновского излучения. При выбивании электрона, например на К-уровень, возможен переход электронов с L-уровня (появляется Кα - излучение) или с М-уровня (появляется Кβ -излучение). При этом получается наиболее коротковолновая К-серия рентгеновского спектра (рисунок 2). Однако, вероятность переходов между дальними оболочками значительно меньше, чем между соседними. Поэтому интенсивность спектральных линий, соответствующих β-сериям гораздо меньше, чем интенсивность α-серий. То есть на спектре рентгеновского излучения проявляются, как правило, только α-линии и β-линии. А так как К-оболочка самая глубокая и имеет самый большой энергетический зазор до другой ближайшей оболочки, то при переходах на эту оболочку излучаются кванты самых высоких энергий.
Кроме того, за счет орбитального расщепления оболочек, происходит расщепление линий характеристического рентгеновского излучения. Например, Кα - линия является дублетом, состоящим из Кα1 - линия и Кα2 -линии с разделением δλ/λ
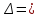 a(cosφ-cosψ) a(cosφ-cosψ) | (1) |
Таким образом, разность фаз, возникающую вследствие разности хода падающей и отраженной волн, в общем виде можно записать как:
 ) ) | (2) |
Очевидно, что максимальная амплитуда рассеянной волны достигается при условии, что волны, рассеянные центрами А и В совпадают по фазе, т.е.
 =
= 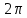 n:
n: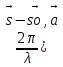 ) =
) = 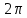 n или
n или 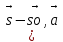 )=n
)=n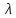
Условие дифракции можно изобразить в виде следующей векторной диаграммы (рисунок 4).
Пусть
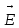 =
= 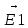 +
+ 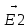 - напряженность электрического поля электромагнитной волны, возникающей в результате суперпозиции электромагнитных волн от двух рассеивающих центров. Максимальная величина
- напряженность электрического поля электромагнитной волны, возникающей в результате суперпозиции электромагнитных волн от двух рассеивающих центров. Максимальная величина 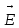 достигается, если оба вектора совпадают по направлению, т.е. при
достигается, если оба вектора совпадают по направлению, т.е. при 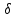 =
= 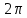 n.
n.Такая векторная диаграмма позволяет легко понять, что будет, если перейти к бесконечному периодическому атомному ряду. В этом случае нужно суммировать вектора
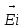 , по бесконечному числу рассеивающих центров. Волны, рассеянные этими атомами в некотором заданном направлении, имеют одинаковую амплитуду колебаний, но каждая последующая отстает по фазе от предыдущей на одну и ту же величину
, по бесконечному числу рассеивающих центров. Волны, рассеянные этими атомами в некотором заданном направлении, имеют одинаковую амплитуду колебаний, но каждая последующая отстает по фазе от предыдущей на одну и ту же величину 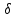 (рисунок 4б).
(рисунок 4б). Если
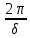 - целое число, на векторной диаграмме будет присутствовать конечное число векторов (любой вектор с разностью фаз больше
- целое число, на векторной диаграмме будет присутствовать конечное число векторов (любой вектор с разностью фаз больше 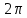 будет совпадать с одним из векторов с разностью фаз меньше
будет совпадать с одним из векторов с разностью фаз меньше 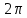 ). Если
). Если 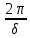 - не является целым числом, вектора
- не является целым числом, вектора 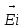 , полностью заполнят круг. В том и в другом случае векторная сумма будет равна нулю. Исключением является случай, когда разность фаз кратна 2
, полностью заполнят круг. В том и в другом случае векторная сумма будет равна нулю. Исключением является случай, когда разность фаз кратна 2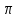 , т.к. при
, т.к. при 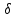 =
= 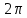 n вектора складываются.
n вектора складываются. 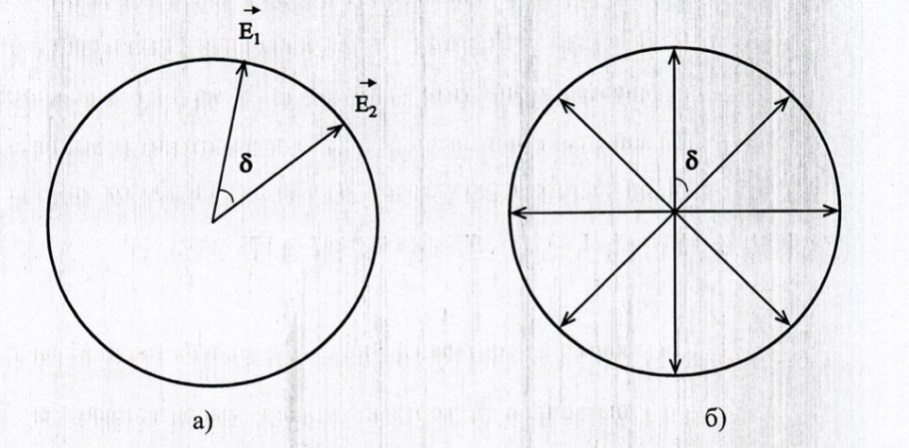
Рисунок 4 - Векторная диаграмма, иллюстрирующая суммирование напряженностей электромагнитных волн, рассеянных
а) двумя центрами; б) N центрами.
Из этого рассуждения следует важное различие между рассеянием двумя центрами и рассеянием бесконечным рядом периодически расположенных центров. В последнем случае интенсивность рассеяния будет отлична от нуля только строго в тех направлениях, для которых
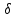 =
= 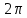 n, в то время как для двух центров интенсивность рассеяния достигает максимума при данном условии, но отлична от нуля и при других значения
n, в то время как для двух центров интенсивность рассеяния достигает максимума при данном условии, но отлична от нуля и при других значения 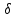 , кроме значений
, кроме значений 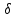 =
= 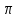 n при нечетных n.
n при нечетных n. Если мы рассмотрим не один атомный ряд, а трехмерный периодический кристалл, то, очевидно, требование кратности разности фаз величине 2
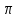 справедливо в отношении любого атомного ряда, и, следовательно, по отношению ко всей трехмерной совокупности (узлов решетки) в целом.
справедливо в отношении любого атомного ряда, и, следовательно, по отношению ко всей трехмерной совокупности (узлов решетки) в целом.Условия дифракции на трехмерной решетке (условия Лауэ)
Рассматривая бесконечную трехмерную периодическую решетку, построенную на векторах
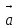 ,
,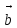 ,
,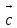 , с учетом (1) можно записать условия возникновения дифракционного максимума (условия Лауэ) в следующем виде.
, с учетом (1) можно записать условия возникновения дифракционного максимума (условия Лауэ) в следующем виде. | a(cosα- cosα0)=p 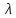 , ,b(cosβ- cosβ0)=q 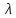 , ,c(cosγ- cosγ0)=r 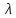 , , | (3а) |
где а, b, с, - модули периодов решетки (параметры решетки),
α0, β0,γ0- углы между векторами
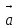 ,
,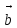 ,
,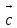 , направлением первичного пучка
, направлением первичного пучкаα, β,γ- углы между
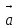 ,
,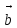 ,
,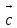 и направлением дифрагированного пучка.
и направлением дифрагированного пучка. Вообще говоря, углы α, β,γ не являются независимыми. Так при
| cos2α+cos2β +cos2γ=1 | (3б) |
Уравнение (3б) дополняет систему уравнений (3а), и тем самым, мы имеем систему четырех уравнений с тремя неизвестными. Это обстоятельство имеет принципиальное значение для практической реализации дифракционного эксперимента. B общем случае (произвольной ориентации кристалла и произвольной длины волны) система уравнений (3) может быть несовместимой и дифракции может не быть. Роль четвертого переменного параметра может играть либо длина волны излучения, либо поворот кристалла относительно первичного пучка.
Отсюда вытекают возможные схемы дифракционного эксперимента:
1. Использование монокристального образца и излучения с широким спектром длин волн (полихроматического излучения) - метод Лауэ. Можно ожидать, что при наличии достаточно широкого спектра для некоторых длин волн будут выполняться условия дифракции (3).
2.Использование монокристального образца и монохроматического излучения (
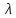 =const) с вращением образца. При некоторых углах поворота кристалла по отношению к падающему пучку будет выполняться условие дифракции для данной длины волны.
=const) с вращением образца. При некоторых углах поворота кристалла по отношению к падающему пучку будет выполняться условие дифракции для данной длины волны.3.Использование поликристаллического образца и монохроматического излучения. Можно ожидать, что в достаточно большом ансамбле мелких случайным образом разнориентированных кристаллитов всегда найдутся кристаллиты с такой ориентацией по отношению к падающему пучку, при которой выполняются условия дифракции (3).
3.2 Закон Брэгга-Вульфа
Рентгеновская дифрактометрия основана на способности рентгеновских лучей отражаться от плоских сеток, образованных атомами в кристаллической решетке материала. Это приводит к возникновению дифракционных отражений (дифракционных максимумов), каждое из которых характеризуется определенным межплоскостным расстоянием и интенсивностью. Возникновение дифракции происходит согласно закону Брэгга-Вульфа.
| nλ = 2d sinθ, | (4) |
где n – целое число, описывающее порядок дифракционного отражения,
λ – длина волны,
d – межплоскостное расстояние между отражающими плоскостями,
θ – угол, который составляет падающий или дифрагированный луч с отражающей плоскостью.
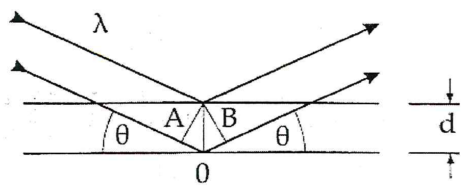
Рисунок 5 - Дифракция плоской волны
Вывод закона Брэгга-Вульфа можно понять с помощью рис. 4, на котором показана схема образования интерферирующих лучей. Отражение получается в случае, когда углы θ падения и отражения равны друг другу и разность хода АОВ между двумя лучами, отражёнными от соседних плоскостей, равна nλ, т.е. целому числу длин волн. Таким образом, условие появления рефлекса выглядит так:
| sinθ = 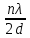 , , | (5) |
где θ - угол падения и отражения рентгеновского пучка от кристаллических плоскостей исследуемого материала.
4 Рентгеновские установки
Установки для рентгеновской дифрактометрии называются рентгеновскими дифрактометрами. Основными составляющими частями дифрактометра являются:
- Источник рентгеновского излучения;
- Гониометр;
- Детектор, регистрирующий дифрагированное излучение.
В лабораторном источнике рентгеновского излучения электроны ускоряются напряжением 20-50 кВ по направлению к твердой мишени, где они тормозятся в результате столкновения. Это приводит к образованию линейчатого спектра на фоне непрерывного (тормозного).
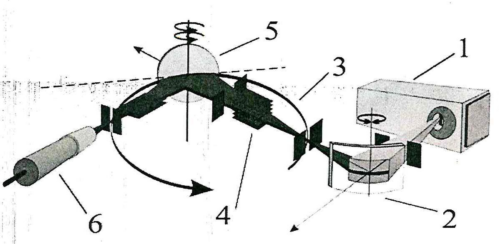
Рисунок 6 - Рентгеновская схема дифрактометра с фокусировкой по Брэггу- Брентано. 1. - рентгеновская трубка, 2. - монохроматор, 3. - гониометр, 4. - щели, 5. - образец, 6. - детектор
Наиболее распространенным лабораторным источником рентгеновских лучей является рентгеновская трубка. Источником электронов является катод - вольфрамовая спираль, нагреваемая электрическим током. При повышении температуры нити накала, количество электронов, испускаемых катодом, возрастает, т.е. сила тока трубки зависит от температуры нити накала (тока накала трубки).
Рентгеновские трубки могут быть запаянными и разборными. На рисунке 7 приведена схема рентгеновской трубки.
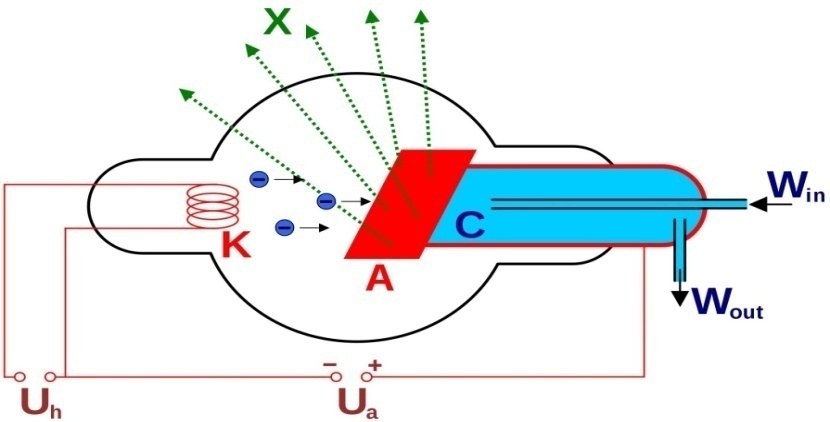
X - рентгеновские лучи, K - катод, А- анод (иногда называемый антикатодом), С - теплоотвод, Uh – напряжение накала катода, Ua - ускоряющее напряжение, Win - впуск водяного охлаждения, Wout - выпуск водяного охлаждения
Рисунок 7 – Схема рентгеновской трубки
Материал анода определяет длину волны рентгеновского излучения. Наибольшее распространение получили медные аноды в силу высокой интенсивности и удобной длины волны, которая соизмерима с большинством межплоскостных расстояний. Кроме того, медную мишень легко охладить по причине её высокой теплопроводности, и её производительность ограничивается только отводом тепла. Охлаждение может быть воздушным, водяным или смешанным в сочетании с вращением анода для более эффективного рассеяния тепла.
Гониометр является основным узлом дифрактометра, на котором установлены детали (щели, монохроматор, держатель образцов), создающие оптимальную геометрию для получения и регистрации дифракционной картины. Гониометр служит для приведения в движение держателя образцов и поворота приёмной щели детектора, а так же для точного отсчёта углов и расстояний. Детекторами служат чаще всего пропорциональные или сцинтилляционные счётчики.
В большинстве дифрактометров, предназначенных для проведения фазового анализа поликристаллических объектов, используется так называемая фокусировка по Брэггу-Бретано, основанная на равенстве вписанных углов, опирающихся на одну и ту же дугу: фокус рентгеновской трубки (F), поверхность образца (Р) и приемная щель детектора (S) должны находиться на одной окружности — окружности фокусировки (рисунок 8). Такая фокусировка позволяет использовать расходящийся первичный пучок рентгеновских лучей и вращать образец в собственной плоскости (для уменьшения эффекта крупнокристалличности исследуемого материала).
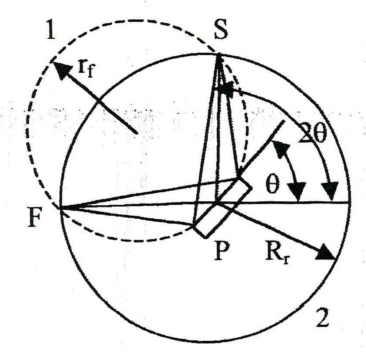
Ход лучей при фокусировке по Бреггу-Брентано. F — фокус рентгеновской трубки, Р - поверхностьобразца и S - приемная щель детектора
Рисунок 8 – Окружность фокусировки
Щели (системы щелей) ограничивают вертикальную горизонтальную расходимость рентгеновского пучка. Монохроматор уменьшает спектральную и/или угловую расходимость, однако, это сопровождается значительным уменьшением интенсивности рентгеновского пучка. Основной задачей в случае поликристаллических образцов является регистрация возможно большего количества дифракционных отражений, поэтому для анализа таких объектов монохроматор, как правило, не используется.
Гониометр обеспечивает одновременный поворот образца на угол θ и поворот детектора на угол 2θ, чтобы всегда выполнялось равенство углов падения и отражения необходимое по условию Брэгга-Вульфа
Таким образом, измерение дифрактограммы осуществляется в режиме θ-2θ сканирования, при котором скорость поворота детектора в два раза больше скорости поворота образца. Особенностью поликристаллического образца, является то, что возможно получить отражения от всех возможных для исследуемого материала кристаллографических плоскостей.
Сканирование производится в широком угловом диапазоне (для 2θ 5° - 100°) с целью зарегистрировать возможно большее количество дифракционных максимумов. Скорость сканирования и шаг определяются решаемой задачей. Рентгенодифракционная кривая в случае поликристаллического образца — дифрактограмма представляет собой зависимость интенсивности дифрагированного рентгеновского пучка от двойного Брэгговского угла 2θ. При этом каждому дифракционному максимуму на дифрактограмме соответствует своё межплоскостное расстояние согласно уравнению Брегга-Вульфа (4).
4.1 Решётка Браве
Решётка Браве - понятие для характеристики кристаллической решётки относительно сдвигов. Названа в честь французского физика Браве.
Браве предположил, что пространственные решётки кристаллов построены из закономерно расположенных в пространстве точек – узлов (мест расположения атомов), которые могут быть получены в результате повторения данной точки путём параллельных переносов (трансляций; рисунок 9). Проведением прямых линий и плоскостей через эти точки, пространственная решётка разбивается на равные параллелепипеды (ячейки).
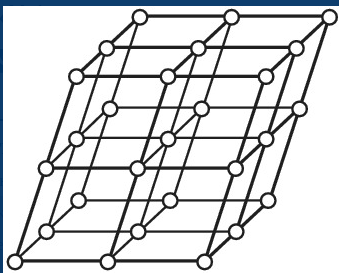
Рисунок 9 - Схема построения пространственной решётки кристалла путём параллельных переносов
Всего существует 14 типов решёток Браве, с помощью которых может быть описана структура любого кристалла. В зависимости от расположения узлов решётки Браве делятся на: примитивные - узлы расположены только в вершинах параллелепипеда; базоцентрированные – узлы расположены в вершинах параллелепипеда плюс ещё по одному узлу в центрах двух противолежащих граней; объёмноцентрированные – узлы расположены в вершинах параллелепипеда плюс узел в центре ячейки; гранецентрированные – узлы расположены в вершинах параллелепипеда плюс по одному узлу в центре каждой грани. В зависимости от симметрии элементарной ячейки Б. р. распределяются по 7 сингониям (рисунок 10).
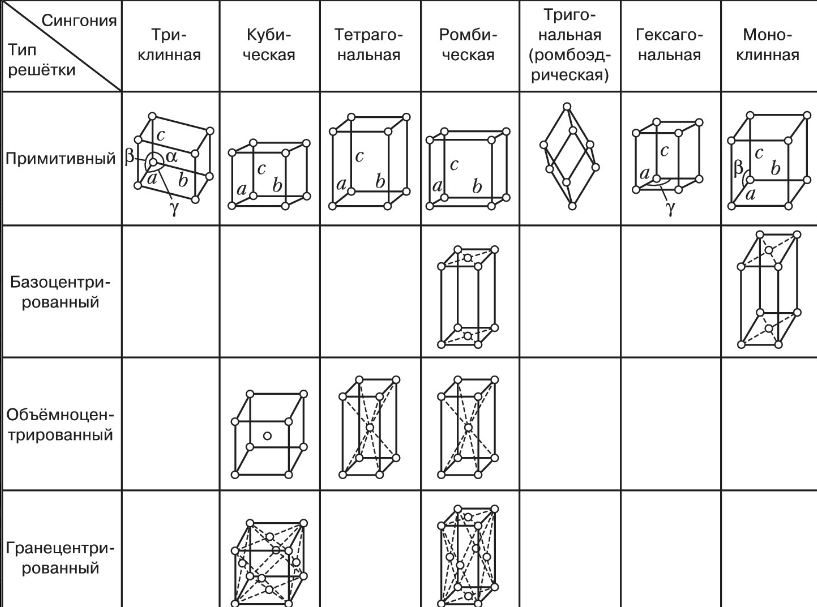
Рисунок 10 - Решётки Браве
4.2 Индексы Миллера
В кристаллографии принято обозначать положения атомов в узлах кристаллической решетки, кристаллографические направления и плоскости с помощью, так называемых, индексов Миллера.
4.2.1 Индексы узла.
Положение любого узла кристаллической решетки относительно произвольно выбранного начала координат определяют заданием его координат (х, у, z) - Для транслируемой элементарной ячейки эти координаты равны периодам решетки а,b с. Для удаленной от начала координат ячейки координаты узла определяют как х = та, у -nb, z —рс, где т, п, р — целые числа.
Если за единицу измерения длин вдоль осей принять величины а,b,с, то координаты узла будут т п р. Они называются индексами узла.
4.2.2 Индексы плоскости.
Для какой-либо плоскости индексы Миллера представляют собой обратные отношения величин отрезков, отсекаемых искомой плоскостью на координатных осях, к трансляциям (единичным отрезкам) элементарной ячейки.
Порядок определения индексов Миллера для любой кристаллографической плоскости следующий:
1) выбирают начало координат (не в данной плоскости);
2) определяют точки пересечения плоскости с координатными осями, измеряют длины отрезков т, п, р, отсекаемых плоскостью на этих осях, в масштабе элементарной трансляции вдоль соответствующей оси;
3) находят обратные значения величин 1 /т, /п, 1 /р
4) приводят их к виду наименьших дробей с общим знаменателем;
5) отбрасывают общий знаменатель и записывают полученные индексы Миллера h, к, I в круглых скобках (hkl).
Если плоскость отсекает на координатных осях отрицательные отрезки, то над соответствующим индексом ставится знак минус.
4.2.3 Индексы направления.
Индексы Миллера для какого-либо направления представляют собой отношения проекций искомой прямой на координатные оси к трансляциям (единичным отрезкам) элементарной ячейки. Если данное направление не проходит через начало координат, то его переносят параллельно самому себе в начало координат. Далее из любой его точки опускают перпендикуляры на координатные оси, и полученные значения уменьшают до простых целых чисел, как в случае нахождения индексов плоскостей.
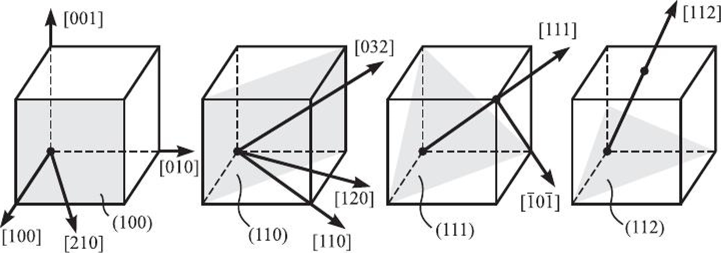
Риунок 11 - Индицирование с помощью индексов Миллера плоскостей и направлений в простой кубической решетке
Индексы направлений обозначают (в соответствии с координатными осями х, у и z) через и, v, w и заключают в квадратные скобки: [uvw]. В случае отрицательного значения, над индексом ставится знак минус.
Для записи с помощью индексов Миллера группы кристаллографически эквивалентных плоскостей и направлений используют соответственно фигурные {} и угловые < > скобки.
Например, семейство плоскостей (100), (010), (001), (100) может быть обозначено как {100}, а направлений [111], [111], [11 1], [И 1] — как < 111 >.
На рисунке 11 даны примеры индицирования кристаллографических плоскостей и направлений в простой кубической решетке.
4.3 Сингонии
Сингония — одно из подразделений кристаллов по признаку формы их элементарной ячейки. Сингония включает группу классов симметрии, обладающих одним общим или характерным элементом симметрии при одинаковом числе единичных направлений. Различают семь сингоний: кубическую, тетрагональную (квадратную), тригональную, гексагональную, ромбическую, моноклиническую, триклиническую.
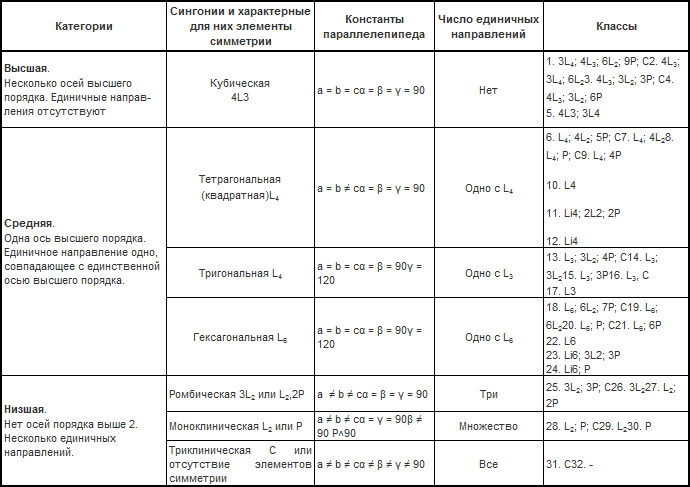
Рисунок 12 - Классификация кристаллов по степени симметрии
В тетрагональной (квадратной) сингонии общим элементом симметрии является L4. Обычно у кристаллов этой сингонии есть квадратное поперечное сечение и одно единичное направление, совпадающее с L4. Кубическая сингония отличается наибольшей степенью симметрии. Общим элементом является 4L3. Единичные направления отсутствуют, все направления симметрично равные. Кристаллы равномерно развиты по всем направлениям, фигуру можно вписать в шар. Такая форма называется изометричной.
В гексагональной и тригональной сингониях единичное направление совпадает с L6 (у гексагональной сингонии) или с L3 (у тригональной системы). Общим элементом симметрии для кристаллов гексагональной сингонии является ось L6, а для кристаллов тригональной сингонии – L3. Кристаллы гексагональной сингонии в сечении имеют шестиугольник, а кристаллы тригональной сингонии – треугольник.
В ромбической сингонии отсутствуют оси симметрии выше второго порядка. Общим элементом симметрии является 3L2 или L2, 2Р. Единичных направлений три. Кристаллы в сечении имеют ромб.
В моноклинальной сингонии каждый элемент симметрии присутствует в кристалле в единственном числе. Единичных направлений много. Общим элементом симметрии является L2 или Р.
В триклинической сингонии из всех элементов симметрии может присутствовать только центр С. Все направления в кристалле единичные.
Сингонии группируются в три категории:
Высшая – единичные направления отсутствуют, всегда имеется несколько осей порядка выше двух; сюда относится кубическая сингония.
Средняя – имеется одно единичное направление, совпадающее с единственной осью порядка выше двух (с осями L3, L4, L6). К этой категории относятся тетрагональная, тригональная и гексагональная сингонии.
Низшая – имеется несколько единичных направлений, отсутствуют оси симметрии выше двух; сюда относятся триклиническая, моноклинальная и ромбическая.
5.Рентгенографический метод контроля в металлографии
Радиографический контроль (рентгенографический, радиационный) — это один из методов неразрушающего контроля, направленного на проверку объектов с целью выявления дефектов, которые невозможно обнаружить при помощи визуального осмотра, то есть скрытых изъянов и нарушений структуры материала. Радиографический контроль осуществляется благодаря способности рентгеновских волн к глубокому проникновению в толщу различных материалов.
Как источник излучения в рентгеновском оборудовании используются такие вещества, как изотопы иридия 192, кобальт-60, в некоторых случаях применяют Цезий-137. Волны способны проходить объект насквозь, а значит рентгеновское излучение, принятое и зафиксированное с противоположной стороны объекта, можно подвергнуть обработке и получить информацию о толщине и составе материала. Установленная норма для длины волны проникающего излучения, как части электромагнитного спектра, в процессе радиографического контроля должна быть менее 10 нм.
Радиографический метод практикуется при выявлении в сварных соединениях и швах пор, трещин, непроваров, окисных, вольфрамовых, шлаковых и других включений. Этот способ используют также для обнаружения прожогов и подрезов. Радиационный метод позволяет определить величину выпуклости и вогнутости корня сварного шва, недоступного при внешнем осмотре.
Радиографическая дефектоскопия считается самым достоверным и точным способом контролирования сварных соединений и основного металла. Данный вид контроля нашел широкое применение в промышленной и строительной сферах при диагностике технологических трубопроводов, металлоконструкций, производственного оборудования, композитных материалов. Радиографический контроль сварных соединений и швов (радиационная дефектоскопия) проводится согласно требованиям ГОСТ Р 7512-86 «Контроль неразрушающий. Соединения сварные. Радиографический метод».
Принцип действия рентгеновского контроля — поглощение рентгеновских лучей, зависимое от плотности среды и атомного номера элементов, которые образуют материал объекта. Лучи, проникая сквозь различные дефекты (трещины, раковины, включения инородных материалов), в различной степени ослабляются. При регистрации распределения интенсивности проходящих лучей, определяется факт наличия и расположение различных неоднородностей и дефектов.
Рентгеновский контроль эффективен для обнаружения раковин, грубых трещин, включений в литых и сварных стальных объектах, которые имеют толщину свыше 90 мм, а также в конструкциях из лёгких сплавов, имеющих толщину до 250 мм. На объектах с такими параметрами контроль осуществляется промышленными рентгеновскими установками с энергией излучения от 5-10 до 200-400 кэВ (1 эв = 1,60210 Ї 10-19 Дж). Изделия, имеющие большую толщину (до 500 мм), диагностируют сверхжёстким электромагнитным излучением, энергия которого достигает десятков МэВ (получают в бетатроне).
5.1 Преимущества рентгенографического контроля
Преимущества рентгенографического контроля:
выявление дефектов (непроваров, раковин), которые невозможно обнаружить при помощи других методов;
точность определения локализации дефекта, что позволяет быстро и эффективно провести ремонтные работы;
объективная оценка величины выпуклости и вогнутости валиков усиления сварных соединений;
осуществление контроля возможно для различных материалов: металлов, сплавов, минералов, неорганических и органических соединений, полимеров, аморфных веществ;
благодаря рентгенографическому контролю возможно максимально полное покрытие вероятных технологических дефектов.
При этом радиографический контроль имеет свою специфику. Такой метод будет эффективен только при соблюдении ряда условий:
должны быть установлены оптимальные режимы;
правильно определены геометрические параметры: размер фокусного пятна трубки, расстояние от контролируемого объекта до преобразователя излучения, фокусное расстояние;
заданы верные физические свойства, такие, как напряжение и ток рентгеновской трубки.
Рентгенографический контроль должен осуществляться квалифицированными и аттестованными, в соответствии с требованиями, операторами. РГК предусматривает наличие высокого уровня профессионализма, а также специальных знаний и навыков. Радиографический (радиационный) контроль качества проводится своими силами непосредственно на производстве, если речь идет о крупном предприятии. В некоторых случаях для РГК привлекаются специализированные организации, имеющие соответствующую лицензию.
Заключение
Открытие рентгеновского излучения предоставило возможность изучать природу веществ и совершать научные прорывы в различных областях. Рентгеновское излучение нашло свое применения практически во всех отраслях: в медицине обследуется тело человека, в нефтегазовом деле проводить качественный контроль оборудования, в науке изучаются объекты исследования, проверяются выдвинутые гипотезы, фиксируются результаты экспериментов и т.д.
Использование рентгеновских дифракционных методов исследования позволяет изучать структуру кристаллических веществ: определять межплоскостные расстояния, индексы интерференции, сингонию, параметры элементарной ячейки, группу симметрии, координаты атомов в структуре. Наряду со структурными характеристиками идеального кристалла можно получить информацию о дефектности структуры: количестве и типе точечных дефектов, количестве и ориентировке дислокационных петель, характеристики напряженного состояния материала.
Основные задачи, решаемые рентгеновским дифракционным методом:
1) идентификация фазы;
2) определение строения твердых растворов;
3) исследование диаграмм;
4) фазовые и полиморфные переходы;
5) внешние воздействия (термодеформационная обработка);
6) выявление реальной структуры;
7) определение координат структуры;
8) изучение распределения электронной плотности.
Выводы.

 показывает направление падающей волны. В общем случае волна падает не перпендикулярно к АВ, а под углом
показывает направление падающей волны. В общем случае волна падает не перпендикулярно к АВ, а под углом 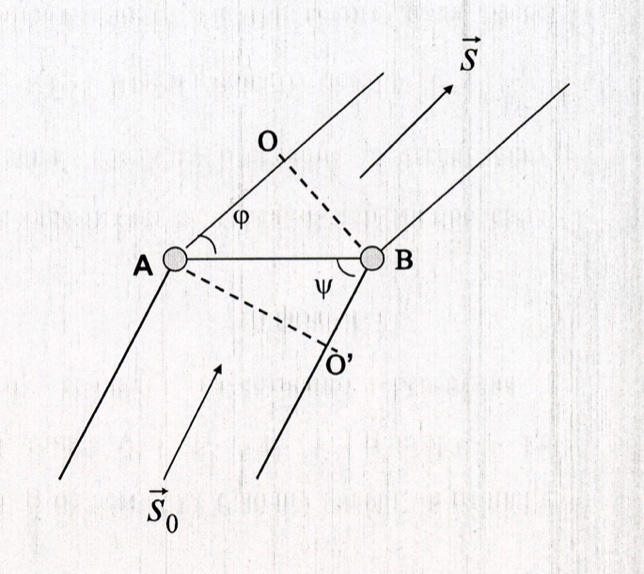
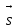 полностью погасят друг друга. Очевидно, что разность хода (в обозначениях рисунка 1) складывается из отрезков АО и О'В.
полностью погасят друг друга. Очевидно, что разность хода (в обозначениях рисунка 1) складывается из отрезков АО и О'В. 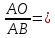 cos
cos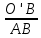 = cos
= cos