Ибатуллаев Рафаэл. В части безопасности жизнедеятельности рассмотрены вопросы по созданию благоприятных условий труда
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
Расчет и построение продольного профиля пролета РРЛ Кулсары – АтырауПродольный профиль интервала выполнена в масштабе вертикальный разрез земле вдоль линии, соединяющей две соседние станции реле. Интервалы полные РРЛ продольные профили и четко характеризуют почву в каждом интервале и связи являются основными рабочими документами, обеспечивает оценку устойчивости линии радиорелейной связи с правилами, изложенными в его качественных показателей. Построение профилей выполняется в прямоугольной системе координат с использованием различных масштабах в горизонтальной и вертикальной. Высота препятствий на поверхности Земли измеряется в метрах, а расстояние между Радиоретранслятор станций - в километрах. Таким образом, профиль высоты не на хранение в прямых, проходящих через центр Земли (то есть, радиус Земли), и по вертикали (ось у) и счет не заблокирован горизонтальной линии профиль, и линии кривизны поверхности Земли, взял на линии уровня моря или условного нуля. Расстояния между станциями не осаждается на изогнутой поверхности, а по горизонтальной (ось х). В этой конструкции, профиль поверхности земли не представлен окружности и параболы. Строительство кривизна дуги земли (параболы) выполняется после определения расстояния между станциями и максимальной разностью высот на земле, как функция расстояния изменяет масштаб по вертикали. Расстояния между станциями и самой низкой (HMIN) и (Hmax) указывают диапазон высокая ссылки радиорелейных профиль определяется с использованием топографических карт, а затем вычисляет максимальную разницу в высоте в метрах . После выбора масштаб строит дугу кривизны Земли.Линия, изображающая на профиле уровень моря (дуга земной кривизны) или условный нулевой уровень (условный горизонт) и имеющая вид параболы, рассчитывается по формуле R 0R R x(R) 1 2R 3 R , (3.1) 0 где x(R) – текущая координата дуги нулевого уровня, м; R0 – протяженность интервала, км; R – расстояние от левого конца интервала, км, до точки, в которой определяется величина x; RЗ=6,37·106 м – радиус Земли. Максимальная высота препятствия, создаваемого выпуклостью земной поверхности, для любой протяженности интервала R0 при R=R0/2 равна x МАКС R 0 2 / 8RЗ . (3.2, а) С достаточной для практических расчетов степенью точности при Rз=6370км можно принять  МАКС 0 x 1,96102 R 2 , (3.2, б) где R0 выражено в км Для сокращения размеров чертежа высокие отметки отсчитываются от линии условного горизонта, которая выбирается в зависимости от рельефа местности. Полученная кривая характеризует профиль интервала данного участка связи. Выбор оптимальных высот подвеса антенн Из-за неравномерности вертикального градиента диэлектрической проницаемости атмосферы радиолуч получает искривление, что приводит к ухудшению радиосвязи. Если он встречается с естественным препятствием, то связь нарушается. Поэтому необходимо правильно определить просвет трассы путем правильного выбора высот подвеса антенн. Радиолуч перемещается внутри зоны Френеля, которая представляет собой эллипсоид вращения в точке приема и передачи. Минимальный радиус зоны Френеля определяется по формуле 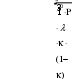 H0 , (3.3) H0 , (3.3)где c / f длина волны, м; k R(H max ) R0 относительное расстояние до препятствия. Среднее значение изменения просвета за счет рефракции, существующее в течение 80% времени, вычисляется по формуле H(g  R 0 R 2 ) 0 (g R0 ) k (1 k) , (3.4)   R 0 где g и – соответственно среднее значение и стандартное отклонение вертикального градиента проницаемости (см. таблицу 3.1). Т а б л и ц а 2.1 – Среднее значение и стандартное отклонение вертикального градиента проницаемости
При длине пролета меньше 50 км стандартное отклонение должно определяться по формуле 8 g 1  R 10 10 0 1 , (3.5) 3,1 y y где – значение стандартного отклонения, м-1; y – находится по рисунку 3.3. 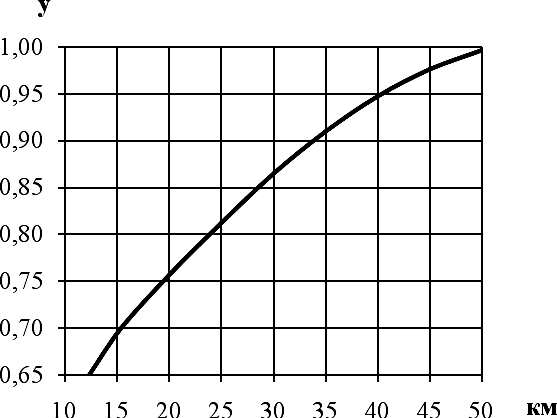 Рисунок 3.3 К определению параметра «y» Рассчитываем просвет в отсутствии рефракции радиоволн (при g=0) по формуле  0 H(0) H0 H(g R ) , (2.6) Рассчитываем кривизну земли х=1,96 ∙10-2 ∙ R02 = 1,96∙10-2 ∙ 232 = 10,4 м Определяем минимальный радиус зоны Френеля k 27 0.75, 35 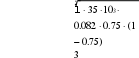 H0 H0 9,52 м.  Рисунок 3.4 – Окно расчета программы Delphi Находим среднее значение изменения просвета за счет рефракции  R 2 H(g σR ) 0 (g σR ) k (1- k) , (3.7) 0 4 0 где y = 0,8 σ (10 10-8 g ) ( 1 1) σ R0 -8 7 108 3.1 y y 1 9 10-8 8 1 (3.8) |
