Подготовка к ОГЭ по математике. Прототипы задания 11. Чтение графиков функций с ответами. Чтение графиков функций

• Название: Чтение графиков функций
• Анкор: Подготовка к ОГЭ по математике. Прототипы задания 11
• Дата: 18.03.2023
• Размер: 0.79 Mb.
• Имя файла: Чтение графиков функций с ответами.docx
• Тип: Решение; #998742
• страница: 1 из 4

Чтение графиков функций

1. Найдите значение 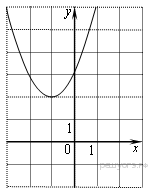  по графику функции  , изображенному на рисунке.



 

1)

2)

3)

4)

Решение.

Абсцисса вершины параболы равна −1, поэтому   откуда   Парабола пересекает ось ординат в точке с ординатой 3, поэтому   Тем самым, уравнение параболы принимает вид   Поскольку парабола проходит через точку (−1; 2), имеем:

 



 

Верный ответ указан под номером 2.

 

Ответ: 2.

2. Найдите значение   по графику функции  , изображенному на рисунке.



 

1)

2)

3)

4)

Решение.

Абсцисса вершины параболы равна −1, поэтому   откуда   Парабола пересекает ось ординат в точке с ординатой 3, поэтому   Тем самым, уравнение параболы принимает вид   Поскольку парабола проходит через точку (−1; 2), имеем:

 



 

Таким образом,



 

Верный ответ указан под номером 3.

 

Ответ: 3.

3. Найдите значение   по графику функции   изображенному на рисунке.

1)

2)

3)

4)

Решение.

Значение   — это ордината графика при   Значит,   Такой ответ указан под номером 4.

 

Ответ: 4.

4. Найдите значение 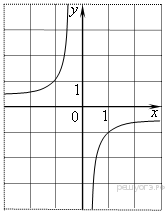  по графику функции   изображенному на рисунке.



Решение.

Поскольку гипербола проходит через точку (−1; 1), имеем: 

 

Ответ: −1.

5. На рисунке изображён график функции 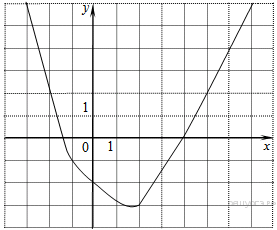  . Какие из утверждений относительно этой функции неверны? Укажите их номера.



 

1) функция возрастает на промежутке  

2) 

3) 

4) прямая     пересекает график в точках     и  

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке    — неверно, функция убывает на промежутке   и затем возрастает на  .

2)   — неверно,   

3)   — верно, видно из графика.

4) Прямая     пересекает график в точках     и    — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

 

Ответ: 12.

6.

На рисунке изображён график квадратичной функции y = f(x).

Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.

 

1) Функция возрастает на промежутке (−∞;  −1].

2) Наибольшее значение функции равно 8.

3) f(−4) ≠ f(2).

Решение.

Проверим каждое утверждение.

1) На луче (−∞;  −1] большему значению аргумента сответствует большее значение функции. Следовательно, функция возрастает на этом луче; первое утверждение верно.

2) Наибольшее значение функции равно 9. Второе утверждение неверно.

3) Значения фунцкии в точках −4 и 2 равны нулю, поэтому f(−4) = f(2). Третье утверждение неверно.

 

Ответ: 23.

7.

На рисунке изображён график квадратичной функции y =  .

Какие из следующих утверждений о данной функции неверны? Запишите их номера.

 

1)   = 

2) Наибольшее значение функции равно 3.

3)   при 

Решение.

Проверим каждое утверждение.

1)   =   Первое утверждение верно.

2) Наибольшее значение функции равно 4. Второе утверждение неверно.

3)   при   Третье утверждение верно.

 

Ответ: 2.

8.

На рисунке изображён график квадратичной функции y = f(x).

Какие из следующих утверждений о данной функции неверны? Запишите их номера.

 

1) Наибольшее значение функции равно 9.

2) f(0)>f(1).

3) f( x )>0 при x<0.

Решение.

Проверим каждое утверждение.

 

1) Наибольшее значение функции равно 9. Первое утверждение верно.

2) Значения фунцкии в точке 0 равно 8, а в точке 1 — 5 поэтому f(0) > f(1). Второе утверждение верно.

3) На луче (−∞;  0) функция принимает как положительные так и отрицательные значения. Третье утверждение неверно.

 

Ответ: 3.

9. На рисунке изображён график функции y = ax² + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.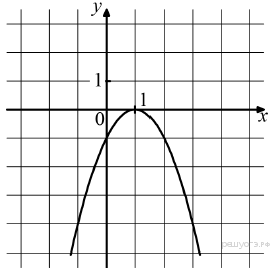



 

 

УТВЕРЖДЕНИЯ		ПРОМЕЖУТКИ
А) функция возрастает на промежутке Б) функция убывает на промежутке		1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3]

 

Ответ:

Решение.

Функция, изображённая на графике возрастает на промежутке   и убывает на промежутке   Следовательно, на данных промежутках функция возрастает на третьем промежутке и убывает на первом.

 

Ответ: 31.

10. На рисунке изображён график функции вида 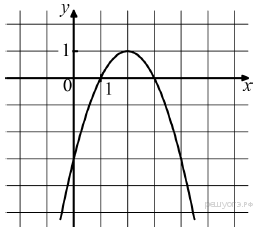 . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

 

УТВЕРЖДЕНИЯ		ПРОМЕЖУТКИ
А) функция возрастает на промежутке Б) функция убывает на промежутке		1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4]

 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: 

А	Б

Решение.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Данная функция возрастает на промежутке   и убывает на промежутке  Таким образом, из приведённых промежутков функция только возрастает на промежутке  убывает на промежутке 

 

Ответ: 23.

11. На рисунке изображены графики функций вида y = ax² + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.

 

Графики

А)

Б)

В)

Г)