|
- Площадки, на которых действуют только нормальные напряжения, а касательные напряжения равны нулю, называются:
|
|
1) тензором;
|
2) нормальными;
|
3) нулевыми;
|
|
4) главными;
|
5) пластическими.
|
|
- Максимальные касательные напряжения действуют на площадках, расположенных к главным осям под углом:
|
1) 00;
|
2) 300;
|
3) 450;
|
4) 600;
|
5) 900.
|
|
-Сдвиговые деформации вызваны:
|
1) касательными напряжениями;
|
2) относительным удлинением;
|
3) нормальными напряжениями
|
4) тензором деформаций;
|
5) упругостью материала.
|
|
- При подъеме груза оборвался канат. Что послужило причиной обрыва?
|
1) недостаточная прочность каната;
|
2) недостаточная жесткость каната.
|
|
- Изменится ли значение внутренних силовых факторов в зависимости от того, будут ли они вычислены по внешним силам, расположенным слева от сечения или справа от него?
|
1) не изменятся;
|
2) изменятся.
|
|
- Расчетная модель
|
1) изготовление макета конструкции;
|
2) изготовление чертежей и эскизов конструкции;
|
3) совокупность аналогий реального объекта при отбрасывании от него второстепенных подробностей, что упрощает расчет.
|
|
- Метод сечений
|
1) метод определения центра тяжести сечения;
|
2) метод выявления внутренних сил в сечении нагруженного тела;
|
|
3) метод определения сил при растяжении – сжатии.
|
|
- Главный вектор внутренних сил равен сумме сил внешних, действующих по одну сторону сечения?
|
1) да;
|
2) нет;
|
3) равен главному вектору внешних сил.
|
|
- Главный вектор внутренних сил определяется методом сечений?
|
1) нет;
|
2) да;
|
3) определяется аналитически.
|
|
- Главный момент внутренних сил определяют моменты изгиба?
|
1) нет;
|
2) да;
|
3) внешние силы.
|
|
- Определите вид деформированного состояния бруса, если в его поперечных сечениях возникает изгибающий момент М и растягивающая сила N?
|
|
1) чистый изгиб;
|
2) растяжение;
|
3) чистый изгиб и растяжение.
|
|
- Можно ли с помощью метода сечений определить закон распределения внутренних сил по сечению?
|
1) можно;
|
2) нельзя.
|
|
- Через любую точку бруса можно провести различные сечения, например, перпендикулярно оси или под углом к ней. Изменится ли величина и направление напряжения в данной точке при изменении направления плоскости сечения?
|
1) не изменится;
|
2) изменится.
|
|
- В чем состоит принцип независимости действия сил?
|
1) Деформации конструкций предполагаются настолько малыми, что можно не учитывать их влияние на взаимное расположение нагрузок до любых точек конструкции.
|
2) Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке.
|
3) Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности.
|
4) Поперечные сечения бруса, плоские до приложения к нему нагрузки, остаются плоскими и при действии нагрузки.
|
|
- Какие внутренние усилия могут возникать в поперечных сечениях брусьев?
|
1) R; M;
|
2) My; Mz; T; N; Qy; Qz;
|
3) T; M;
|
4) My; Mz; T; N; Q.
|
|
- Напряжения нормальные возникают:
|
1) при растяжении – сжатии и изгибе;
|
2) при сдвиге – срезе;
|
3) при статическом нагружении.
|
|
Типы напряжений:
|
1) при ударе;
|
2) при ускоренном движении;
|
3) нормальные(), касательные()
|
|
В наклонном сечении нагруженного стержня осевыми нагрузками возникают:
|
1) силы сдвига;
|
2) нормальные () и касательные напряжения ();
|
3) продольные деформации.
|
|
-При кручении в нормальном сечении вала возникают:
|
1) касательные напряжения;
|
2) нормальные напряжения
|
3) момент сопротивления ().
|
|
- При чистом изгибе в поперечном сечении балки возникают:
|
1) поперечные силы (Q);
|
2) касательные напряжения ();
|
3) нормальные напряжения ().
|
|
- Какую размерность имеют линейные и угловые деформации?
|
1) Линейные деформации измеряются в м, а угловые в рад.
|
2) Линейные и угловые деформации - величины безмерные.
|
3) Линейные деформации- безмерные величины, а угловые измеряются в рад.
|
4) Линейные деформации измеряются в м, а угловые деформации безмерные величины.
|
|
- Основной метод применяемый для определения внутренних усилий.
|
1) метод сил,
|
2) метод перемещений,
|
3) метод сечений.
|
|
- Упругость
|
1) способность материала изгибаться;
|
2) способность материала восстанавливать свою форму и размеры после снятия внешней нагрузки;
|
3) характеристика пружин и рессор.
|
|
- Пластичность
|
1) способность материала приобретать остаточные пластические неисчезающие деформации;
|
2) свойство пластических масс при нагревании;
|
3) способность материала при ковке принимать необходимые формы.
|
|
- Пластичность характеризуется:
|
1) пределом пропорциональности;
|
2) пределом текучести;
|
3) коэффициентом остаточного удлинения () и остаточного сужения шейки () испытуемого образца.
|
|
- Твердость материала:
|
1) способность материала к механической обработке;
|
2) способность материала противодействовать механическому проникновению в него инородных (посторонних) тел;
|
3) свойства, присущие твердым сплавам и алмазу.
|
|
- Характеристики механической прочности:
|
1) модули упругости Е и G;
|
2) коэффициент Пуассона;
|
3) пределы пропорциональности , упругости , предел текучести , предел прочности .
|
|
- Какие механические характеристики материалов вы знаете.
|
1) коэффициент Пуассона,
|
2) предел упругости,
|
3) предел текучести,
|
4) предел жесткости,
|
5) предел прочности,
|
6) предел изогнутости,
|
7) предел пропорциональности.
|
|
- Какие пластические характеристики материалов вы знаете.
|
1) растянутость,
|
2) относительное остаточное растяжение,
|
3) сдвинутость,
|
4) относительное остаточное сужение.
|
|
- Что характеризует допускаемое напряжение.
|
1) прочность,
|
2) жесткость,
|
3) долговечность работы материала.
|
|
- Предельные напряжения:
|
1) напряжения, при которых начинается разрушение (хрупкое и пластичное);
|
2) напряжение, при котором относительное удлинение составляет 0,5%;
|
3) напряжение при коэффициенте запаса n = 1.
|
|
- Напряжение допускаемое (максимальное), , :
|
1) всякое напряжение меньше предела пропорциональности;
|
2) напряжение, равное временному сопротивлению;
|
3) предельное напряжение, деленное на коэффициент запаса.
|
|
- Коэффициент запаса:
|
1) отношение предельного напряжения к максимальному допустимому напряжению;
|
2) безразмерная величина больше 1;
|
3) отношение нормального напряжения к касательному.
|
|
- Каковы последствия увеличения коэффициента запаса?
|
1) вес конструкции уменьшается;
|
2) вес конструкции увеличивается;
|
3) вес конструкции не изменяется.
|
|
-Коэффициент запаса используют для определения допускаемых напряжений
|
1) нет;
|
2) да;
|
3) для увеличения веса конструкции.
|
|
- Справедлив ли закон Гука за пределом пропорциональности
|
1) нет
|
2) да, при наклёпе
|
3) справедлив за пределом прочности
|
|
- Коэффициент Пуассона одинаков при растяжении – сжатии
|
1) да;
|
2) нет;
|
3) неодинаков до предела текучести.
|
|
- Механические характеристики хрупких и пластичных материалов численно отличаются
|
1) да,
|
2) одинаковы при сжатии,
|
3) неодинаковы при нагревании.
|
|
- Предельные напряжения:
|
1) , ;
|
2) , ;
|
3) , .
|
|
- Образцы из стали и дерева с равной площадью поперечного сечением растягиваются одинаковыми силами. Будут ли равны возникающие в образцах усилия?
|
1) в стальном образце возникнут большие напряжения, чем в деревянном;
|
2) в образцах возникнут равные напряжения.
|
3) нет правильного ответа, необходимо знать механические харатеристики
|
|
- Допускаемое напряжение при расчете на прочность было принято равным 180 МПа. После окончательного выбора размеров конструкции рабочее напряжение стало равным 185 МПа. Грозит ли конструкции опасность разрушения?
|
1) да;
|
2) нет.
|
|
- Как изменится масса конструкции, если при подборе ее сечения уменьшить коэффициент запаса прочности?
|
1) масса конструкции уменьшится;
|
2) масса не изменится.
|
|
- Сколько связей накладывается на балку со стороны
|
|
1) шарнирно подвижной опоры.
|
5, 4, 2, 3, 1
|
|
2) шарнирно неподвижной опоры.
|
5, 4, 2, 3, 1.
|
|
3) жесткой заделки.
|
5, 4, 2, 3, 1.
|
|
- Вал находится в равновесии при
|
1) ,
|
2) ,
|
3) ,
|
4) .
|
|
- Схема какого напряженного состояния изображена на рисунке?
|
|
1) одноосное растяжение;
|
2) разноименное плоское напряженное состояние;
|
3) двухосное растяжение;
|
4) трехосное растяжение;
|
5) разноименное объемное напряженное состояние.
|
|
Схема какого напряженного состояния изображена на рисунке?
|
|
1) одноосное сжатие;
|
2) двухосное сжатие;
|
3) трехосное сжатие;
|
4) разноименное плоское напряженное состояние;
|
5) разноименное объемное напряженное состояние.
|
|
Схема какого напряженного состояния изображена на рисунке?
|
|
1) одноосное сжатие;
|
2) двухосное сжатие;
|
3) трехосное сжатие;
|
4) разноименное плоское напряженное состояние;
|
5) разноименное объемное напряженное состояние.
|
|
Схема какого напряженного состояния изображена на рисунке?
|
|
1) одноосное сжатие;
|
2) двухосное растяжение;
|
3) трехосное сжатие;
|
4) разноименное плоское напряженное состояние;
|
5) разноименное объемное напряженное состояние.
|
|
Что понимается под напряженным состоянием в точке твердого тела, если оно нагружено внешними силами?
|
|
Объясните понятие тензор напряжений?
|
|
Какие напряжения называются главными?
|
|
Чем характеризуется и как изображается напряженное состояние в точке?
|
|
Какие площадки и какие напряжения называют главными?
|
|
Чем характеризуется деформированное состояние в точке?
|
|
Сколькими параметрами определяется плоское напряженное состояние точки? Назовите эти параметры?
|
|
В каких случаях возникают предельные напряженные состояния у пластичных и хрупких материалов?
|
|
Сформулируйте закон парности касательных напряжений?
|
|
Какие существуют типы напряженного состояния в точке тела, чем они отличаются?
|
|
Что понимается под линейным напряженным состоянием?
|
|
Что понимается под плоским напряженным состоянием?
|
|
Что понимается под объемным напряженным состоянием?
|
|
Какое напряженное состояние называется пространственным (трехосным), плоским (двухосным) и линейным (одноосным)?
|
|
Понятие о сложном напряженном состоянии.
|
|
Дайте определение главных площадок и главных напряжений. Получите выражения для определения положения главных площадок и величин главных напряжений?
|
|
Какие площадки называются главными?
|
|
Соотношение между главными напряжениями.
|
|
Каково правило законов для нормальных и касательных напряжений?
|
|
Чему равна сумма нормальных напряжений, действующих на любых двух взаимно перпендикулярных площадках?
|
|
Что такое главные напряжения и главные площадки? Как расположены главные площадки относительно друг друга?
|
|
Чему равны касательные напряжения на главных площадках?
|
|
Как вычислить максимальные касательные напряжения в точке тела при одноосном напряженном состоянии? По каким площадкам они действуют?
|
|
Как вычислить максимальные нормальные и касательные напряжения при плоском и объемном напряженных состояниях?
|
|
Как связаны главные напряжения и максимальные касательные напряжения при чистом сдвиге?
|
|
Как определить значение главных напряжений при плоском напряженном состоянии?
|
|
Напишите формулы для определения главных напряжений и углов наклона главных площадок.
|
|
Как определить положение главной площадки, по которой действует главное напряжение в общем случае плоского напряженного состояния?
|
|
Чему равны максимальные значения касательных напряжений в случае плоского напряженного состояния?
|
|
Какие площадки называются площадками сдвига и под каким углом они наклонены к главным площадкам?
|
|
Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках?
|
|
Чему равны максимальные и минимальные касательные напряжения (при заданных напряжениях , , ) и по каким площадкам они действуют?
|
|
Докажите свойство парности (взаимности) касательных напряжений и получите выражения для нормального и касательного напряжения в наклонной площадке?
|
|
Какими выражениями определяются величины экстремальных касательных напряжений и как расположены площадки, в которых они действуют?
|
|
Докажите возможность определения напряжений на наклонной площадке, пользуясь кругом напряжений (Мора)?
|
|
Опишите последовательность построения круга напряжений (Мора) и технику определения с помощью его главных напряжений и главных площадок, величин экстремальных касательных напряжений и площадок, в которых они действуют?
|
|
Получите выражения для относительных линейных деформаций по координатным направлениям при объемном напряженном состоянии? Сформулируйте обобщение этих выражений на случай определения линейных деформаций по произвольному направлению при плоском напряженном состоянии?
|
|
Получите выражение относительной объемной деформации в точке через напряжения?
|
|
Докажите, что коэффициент Пуассона не может быть более 0,5?
|
|
Получите выражение удельной потенциальной энергии в точке через главные напряжения?
|
|
Какие напряженные состояния называются предельными?
|
|
Как определяются предельные состояния при линейном напряженном состоянии?
|
|
Почему нельзя экспериментально исследовать предельные состояния при сложных напряженных состояниях (плоском или объемном)?
|
|
Что представляет собой обобщенный закон Гука?
|
|
Какое напряженное состояние в точке считают предельным?
|
|
Какие напряженные состояния в точке называют подобными?
|
|
Напишите формулы обобщенного закона Гука?
|
|
Какая разница между прямой и обратной задачей при исследовании напряженного состояния твердого тела?
|
|
Как можно определить нормальное и касательное напряжения в наклонной площадке с помощью круга Мора?
|
|
Что понимается под обобщенным законом Гука? Как он записывается аналитически?
|
|
Какая зависимость существует между модулями продольной Е и поперечной G упругости?
|
|
На основе какого из допущений, принятых в курсе сопротивления материалов, получен обобщенный закон Гука?
|
|
Что называется полной удельной потенциальной энергией деформации, удельной потенциальной энергией изменения объема и формы?
|
|
Как определяется потенциальная энергия упругой деформации при линейном и объемном напряженном состоянии?
|
|
Из каких составляющих складывается полная потенциальная энергия твердого тела?
|
|
Какой случай плоского напряженного состояния называется чистым сдвигом?
|
|
Напишите закон Гука при сдвиге.
|
|
Докажите, что объемная деформация при чистом сдвиге равна нулю.
|
|
Напишите зависимость между модулем упругости Е и модулем сдвига G.
|
|
Какой случай напряженного состояния называется чистым сдвигом и каковы его особенности?
|
|
Опишите деформацию при чистом сдвиге и сформулируйте закон Гука при сдвиге.
|
|
Что называется модулем упругости при сдвиге и какова его размерность?
|
|
Получите соотношение между упругими постоянными изотропных тел Е, G, v?
|
|
Что называется предельным опасным состоянием материала? Чем характеризуется наступление опасного состояния для пластичных и хрупких материалов?
|
|
Какая точка тела называется опасной?
|
|
Что называется допускаемым напряженным состоянием?
|
|
Почему определение прочности в случаях сложного (плоского или пространственного) напряженного состояния приходится производить на основе результатов опытов, проводимых при одноосном напряженном состоянии?
|
|
Понятие о теориях (гипотезах) прочности.
|
|
Какие теории (гипотезы) прочности применяются наиболее часто?
|
|
Что представляют собой теории прочности?
|
|
Для чего служат теории прочности?
|
|
Сформулируйте первую и вторую теории прочности. Укажите область применения.
|
|
Сформулируйте третью и четвертую теории прочности? Укажите область применения этих теорий.
|
|
Какие теории прочности считаются классическими?
|
|
На каких предположениях основаны первая, вторая, третья, четвертая и пятая теории прочности? Кто является их основоположниками?
|
|
Какие теории прочности считаются рабочими?
|
|
Какая из теорий используется при расчете конструкций из анизотропных материалов?
|
- На основе какого из допущений, принятых в курсе сопротивления материалов, составлены выражения обобщенного закона Гука?
|
1
|
Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке.
|
2
|
Материал конструкции обладает свойством идеальной упругости.
|
3
|
Поперечные сечения бруса, плоские до приложения к нему нагрузки, остаются плоскими и при действии нагрузки.
|
4
|
Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности.
|
- Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках?
|
1. ;
|
2. ;
|
3. ;
|
4. .
|
- Соотношение между главными напряжениями.
|
1. ;
|
2. ;
|
3. .
|
4. нет правильного ответа
|
|
Что называется стержнем?
|
|
Какой вид нагружения стержня называются осевым растяжением (сжатием)?
|
|
Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
|
|
Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
|
|
Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?
|
|
Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
|
|
Как распределены нормальные напряжения в поперечных сечениях центрально растянутого или центрально сжатого стержня и по какой формуле они определяются?
|
|
Получите формулу нормальных напряжений при растяжении сжатии? Какие предпосылки используются при выводе этой формулы?
|
|
Как записывается условие прочности бруса при растяжении (сжатии)? Какие виды задач решаются с помощью условия прочности?
|
|
В каких единицах измеряется напряжение?
|
|
Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
|
|
Как назначаются знаки продольной силы и нормального напряжения?
|
|
Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня?
|
|
Раскройте понятие эпюр продольных сил, нормальных напряжений и перемещений. Для чего они строятся?
|
|
Что показывает эпюра продольной силы?
|
|
Что представляют собой эпюры внутренних силовых факторов? С какой целью их строят?
|
|
Опишите технику построения эпюры продольных сил в брусе, загруженном несколькими сосредоточенными силами по оси бруса?
|
|
Как вычислить значение продольной силы в произвольном поперечном сечении бруса?
|
|
Как вычислить напряжения в поперечном сечение бруса при растяжении и сжатии? Как они распределены по поперечному сечению?
|
|
Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?
|
|
Как определяется удлинение призматического бруса от собственного веса?
|
|
Какое влияние оказывает собственный вес стержня при проектирования сооружения?
|
|
Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?
|
|
Какие деформации бруса называются абсолютными и какие относительными?
|
|
Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?
|
|
Опишите технику определения продольных и поперечных деформаций бруса при растяжении- сжатии?
|
|
Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (= 0,25)
|
|
Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?
|
|
Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?
|
|
Что называется жесткостью поперечного сечения стержня при растяжении (сжатии)?
|
|
Относительные деформации и перемещения.
|
|
Что понимается под жесткостью при растяжении или сжатия стержня?
|
|
Принципы расчета на жесткость.
|
|
Типы задач при расчетах на жесткость.
|
|
Сформулируйте закон Гука для одноосного растяжения сжатия.
|
|
Напишите формулы для абсолютной и относительной продольных деформаций стержня.
|
|
Что происходит с поперечными размерами стержня при его растяжении (сжатии)?
|
|
Что характеризует коэффициент поперечной деформации?
|
|
Что такое коэффициент Пуассона? В каких пределах он изменяется?
|
|
Как определяется коэффициент Пуассона?
|
|
Какая разница между статически определимой и статически неопределимой стержневой системой?
|
|
Какие системы называют статически неопределимыми? Как установить степень статической неопределимости системы?
|
|
В какой последовательности рассчитывают статически неопределимые системы?
|
|
Сколько уравнений статики нужно составить для системы сил, лежащих на одной прямой?
|
|
Сколько уравнений статики нужно составить для системы сил, расположенных как угодно в плоскости, но сходящихся в одной точке?
|
|
Сколько уравнений статики нужно составить для системы сил, расположенных как угодно в плоскости и не сходящихся в одной точке?
|
|
Какое влияние оказывает на стержневую статически неопределимую системы изменение температуры?
|
|
Как учитываются в статически неопределимых стержневых системах монтажные напряжения?
|
|
Как ведется расчет статически неопределимых систем по методу разрушающих нагрузок?
|
|
Объясните метод расчета статически неопределимых стержневых систем по предельному состоянию?
|
|
Во сколько раз (примерно) поперечная деформация меньше продольной при осевом растяжении (сжатии) стальных стержней?
|
|
При проведении испытаний были получены различные значения коэффициента Пуассона для стали: 0,15; 0,28; 0,4. Укажите, какие значения ошибочны?
|
|
Вычислите продольную силу, возникающую в поперечном сечении растянутого стержня, если нормальные напряжения в этом сечении равны 140 МПа, а его площадь составляет 100 мм2?
|
|
Определение нормальных и касательных напряжений на наклонных площадках при растяжении – сжатии. Вывод формулы.
|
|
Вывести формулу определения нормальных напряжений при растяжении сжатии.
|
На рисунке изображён стержень, находящийся под действием растягивающей силы. Большие напряжения возникнут в точке
|
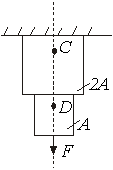
|
1) C;
|
2) D
|
3) напряжения будут одинаковы
|
4) нельзя ответить, не хватает данных задачи
|
- Выберите формулу закона Гука при растяжении (сжатии)?
|
1) ;
|
2) ;
|
3) ;
|
4) .
|
- Что является характеристикой жесткости при растяжении?
|
1) модуль упругости первого рода,
|
2) модуль упругости второго рода.
|
- Условие жесткости:
|
1) рабочее напряжение должно быть меньше временного сопротивления;
|
2) относительная деформация: линейная , угловая ;
|
3) относительная линейная и угловая деформации одинаковы численно.
|
- Выбор сечения из условия жесткости
|
1) сечение должно удовлетворять как условию прочности, так и жесткости;
|
2) сечение должно удовлетворять только условию прочности;
|
3) сечение должно удовлетворять только условию жесткости.
|
- Какие напряжения возникают в поперечном сечении при растяжении (сжатии)?
|
1) сжимающие,
|
2) касательные,
|
3) продольные,
|
4) нормальные,
|
- По формуле определяют:
|
1) напряжение;
|
2) прочность;
|
3) деформацию;
|
4) твёрдость;
|
- Условие прочности при растяжении – сжатии имеет вид:
|
1) ;
|
2) ;
|
3) ;
|
4)
|
- По какой из формул определяется коэффициент запаса прочности для пластичного материала?
|
1) ;
|
2) ;
|
3) ;
|
4)
|
- По какой из формул находятся касательные напряжения в любом сечении сжатого стержня?
|
1) ;
|
2) ;
|
3) ;
|
4) .
|
- По какой из приведённых формул определяются нормальные напряжения при растяжении:
|
1) ;
|
2) ;
|
3) ;
|
4) .
|
- В каких единицах измеряются нормальные и касательные напряжения?
1) Н/м3;
|
2) МПа;
|
3) кН/м;
|
4) нет правильного ответа.
|
- Закон Гука при растяжении–сжатии имеет вид:
- Разделив абсолютное удлинение стержня на его относительное удлинение, что мы получим:
- Два сжатых стержня, равные по размерам, имеют разную жёсткость (у I-го она больше). Различны ли их модули Юнга?
1) нет. ;
|
2) да. ;
|
3) да. ;
|
4) да. .
|
- Условие жёсткости при растяжении – сжатии:
- Какие напряжения возникают в поперечном сечении при центральном растяжении – сжатии?
1) касательные;
|
2) нормальные;
|
3) и ;
|
4) и .
|
- Полная деформация образца состоит из:
1) упругой и пластической;
|
2) пластической;
|
3) только упругой.
|
|
- Если продольная сила N вызывает сжатие, то она считается:
1) положительной;
|
2) отрицательной;
|
3) нет правильного ответа.
|
|
- Какой зависимостью связано полное напряжение с составляющими и ?
1) ;
|
2) ;
|
3) ;
|
4) нет правильного ответа.
|
- Отношение относительной поперечной деформации к относительной продольной деформации называется:
1) коэффициентом Пуассона;
|
2) модулем упругости;
|
3) первоначальной длиной стержня;
|
4) абсолютным удлинением.
|
- Известно, что материалы по-разному работают на растяжение – сжатие. У каких материалов меньше различий?
1) у пластичных;
|
2) у хрупких;
|
3) нет различия.
|
|
- По какой из формул определяется коэффициент запаса прочности для хрупкого материала?
- Как вычисляются нормальные напряжения в наклонных сечениях центрально растянутого, или сжатого бруса?
- Какие перемещения получают поперечные сечения стержня при растяжении–сжатии?
1) линейные;
|
2) угловые;
|
3) линейные и угловые.
|
|
- График, показывающий изменение величины напряжений по высоте или ширине поперечного сечения называют:
1) эпюрой напряжений;
|
2) эпюрой моментов;
|
3) эпюрой сил.
|
|
- Величина коэффициента Пуассона колеблется в интервале:
- Отношение абсолютного удлинения к первоначальной длине бруса называется:
1) относительной продольной деформацией;
|
2) модулем упругости;
|
3) относительной поперечной деформацией;
|
4) полным удлинением .
|
- Указать выражение, соответствующее жёсткости сечения при растяжении–сжатии.
- Допускаемое нормальное напряжение для пластичных материалов определяется:
- Каким соотношением может быть выражена сила «N» через нормальные напряжения?
1) ;
|
2) ;
|
3) нет правильного ответа.
|
|
- Какие свойства материала характеризует коэффициент Пуассона?
1) остаточные;
|
2) пластические;
|
3) упругие.
|
|
- Абсолютное удлинение выражается формулой:
1) ;
|
2) ;
|
3);
|
4) нет правильного ответа.
|
- Сколько внутренних силовых факторов возникает в поперечных сечениях прямого бруса при центральном растяжении (сжатии)?
1) два;
2) один;
3) отсутствуют;
- Если продольная сила N вызывает растяжение, то она считается:
1) положительной;
2) отрицательной;
3) нет правильного ответа.
- Относительное удлинение определяют по формуле:
- Какому напряженному состоянию соответствует кольцевое сжатие образцов по боковой поверхности ?
1) двухосное растяжение;
|
2) двухосное сжатие;
|
3) разноимённое плоское напряжённое состояние;
|
4) трёхосное растяжение;
|
- Закон Гука определяет прямую пропорциональность между упругой деформацией и:
1) пластической деформацией;
|
2) скоростью приложения нагрузки;
|
3) коэффициентом Пуассона;
|
4) напряжением;
|
- Что определяют модули упругости?
- Физический смысл модулей упругости состоит в том, что они характеризуют:
1) отношение продольной относительной деформации к поперечной;
2) относительное удлинение в упругой области;
3) сопротивляемость металлов смещению атомов из положений равновесия в решётке;
4) скорость уменьшения напряжения по мере упругой деформации;
5) обратную пропорциональность между напряжением и упругой деформацией.
- Полная работа на пластическую деформацию равна:
1) ;
2) ;
3) ;
4);
5) .
- Как определяются напряжения при осевом растяжении (сжатии)?
- Что характеризует жесткость при растяжении (сжатии)?
1) модуль упругости второго рода,
|
2) модуль упругости первого рода,
|
3) коэффициент Пуассона.
|
|
- Какие характеристики связывает закон Гука при растяжении (сжатии)?
1) силу и напряжение,
|
2) касательное и нормальное напряжение,
|
3) напряжение и деформацию.
|
|
|
 Скачать 0.84 Mb.
Скачать 0.84 Mb.
