реферат мартынюк. В древнем Китае уже пользовались десятичной системой мер
 Скачать 23.26 Kb.
|
|
Введение Математика - одна из древнейших наук, и ее первые шаги связаны с первыми же шагами человеческого разума. Она возникла в трудовой деятельности людей. Развиваясь, математика все точнее и точнее решала те сложные задачи, которые ставила перед человеком сама жизнь. В трудное положение в 17 веке попала торговля, все производство, экономика стран. Для мореплавателей нужны были точные карты, для купцов быстрые и правильные расчеты без обмана, для строительства станков, кораблей, храмов и жилищ – выверенные до 1мм чертежи. Производство развивалось, а неумение быстро и с большей точностью производить расчеты буквально тормозило развитие науки и техники. Жизнь ставила перед учеными задачу упростить вычисления, увеличить их точность и скорость. Этим требованиям удовлетворяли десятичные дроби. К десятичным дробям математики пришли в разные времена в Азии и в Европе. Зарождение и развитие десятичных дробей в некоторых странах Азии было тесно связано с метрологией (учением о мерах). Уже во II в. до н.э. там существовала десятичная система мер длины. В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Первое упоминание о них относят к третьему веку нашей эры — они появляются в «Математическом трактате» Сунь-Цзы. В средневековой Европе их впервые использовал нидерландский математик Симон Стевин в шестнадцатом веке. В 1585 году он выпустил свой труд “Десятая”, в котором впервые говорил о десятичных дробях, разработал правила арифметических действий с ними и предложил десятичную систему денежных единиц, мер и весов. В 1601 году книга была опубликована в Англии — так и началось путешествие нового способа исчисления по миру. Изначально в качестве знака, отделявшего целую и дробную части, использовалась точка — родоначальником этого “тренда” стала Англия и, в частности, математик Джон Непер. В 1617-м году он же предложил заменить точку запятой. К слову, в Соединенных Штатах для этих целей до сих пор используют точку. Десятичные дроби стали спасением при громоздких вычислениях. Поэтому неудивительно, что наибольшее распространение и “вторую жизнь” они получили в девятнадцатом веке — во время расцвета промышленности, торговли, науки и техники. 1. Определение десятичных дробей и их нумерация В теоретической арифметике десятичные дроби чаще всего рассматриваются как частный случай систематических дробей . Систематической дробью по основанию g называется дробь со знаменателем g m, где m – любое натуральное число, притом записанная по принципу поместного значения цифр без знаменателя. Например, если g 10 , то получается систематическая десятичная дробь, равная обыкновенной дроби 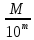 , допускающая запись без знаменателя: где a и z со значками означают одну из цифр 0, 1, 2, ..., 9. 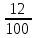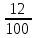Придерживаясь такого определения, получаем, что дробь  – обыкновенная, а дробь 0,12 – десятичная, а записи и 0,12 – разные формы записи одного и того же числа. Однако иногда десятичной дробью называют всякую дробь со знаменателем 10m в независимости от того, как она записана.Первое определение: «Десятичной дробью называется дробь, у которой знаменатель – число, изображенное единицей с последующими нулями» или «Дробь, знаменателем которой является степень числа 10, называется десятичной», т.е. десятичная дробь – частный случай обыкновенной дроби. Во втором определении добавляется условие особой записи, например: «можно представить в виде десятичной записи» или «можно записать в строчку без знаменателя». ОСНОВНАЯ ТЕОРИЯ: 6 слайд. Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая. Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля. 7слайд. Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0,7 семерка – это десятые доли, в 0,0007 – десятитысячные, а в дроби 70 000,345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа. 8 слайд. 9 слайд. конечные десятичные дроби Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. 10 слайд Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр. 11слайд Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби. К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр. Действия над десятичными дробями 1. Сложение (вычитание) десятичных дробей При сложении (вычитании) десятичных дробей пользуются следующим правилом: а) уравнивают количество знаков после запятой в обеих дробях (с помощью нулей); б) записывают дроби друг под другом так, чтобы запятая оказалась под запятой; в) выполняют действие, не обращая внимания на запятую; г) подставляют в результате запятую под запятыми в данных дробях Пример : Сложить 5,607 и 4,1 1. Уравниваем количество знаков после запятой в обеих дробях: 5,607 и 4,100 2. Записываем дроби друг под другом так, чтобы запятая оказалась под запятой:
|