Экзамен. ОТВЕТЫ. В форме громеки
 Скачать 1.4 Mb.
|
|
ОУМ №1 – «Теоретические основы рабочих процессов в энергомашиностроении» Механика жидкости и газов 4. Уравнения динамики для невязкой жидкости (для сжимаемой и несжимаемой). Начальные и граничные условия. ГЛЕБОВ ОТВЕТ Уравнения движения невязкой жидкости В ФОРМЕ ГРОМЕКИ Профессором Казанского университета И.С.Громекой в 1881 г. уравнения Эйлера были преобразованы и записаны в иной форме. Рассмотрим уравнения (4 2). В первом из них вместо  и подс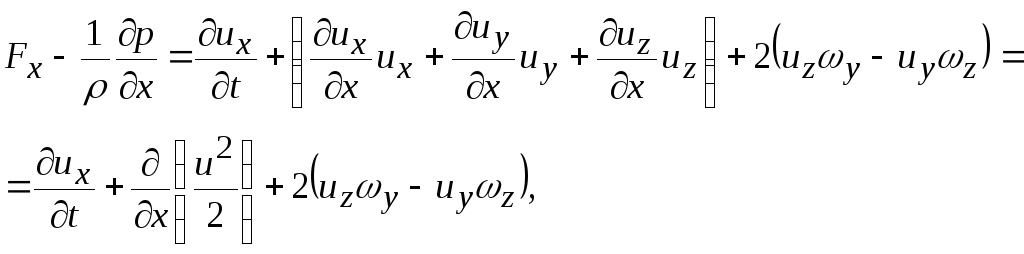тавим их выражения из (3 9): и  .Тогда  где  .Аналогично преобразовав два других уравнения системы (4.2), получим уравнения в форме, данной Громекой: 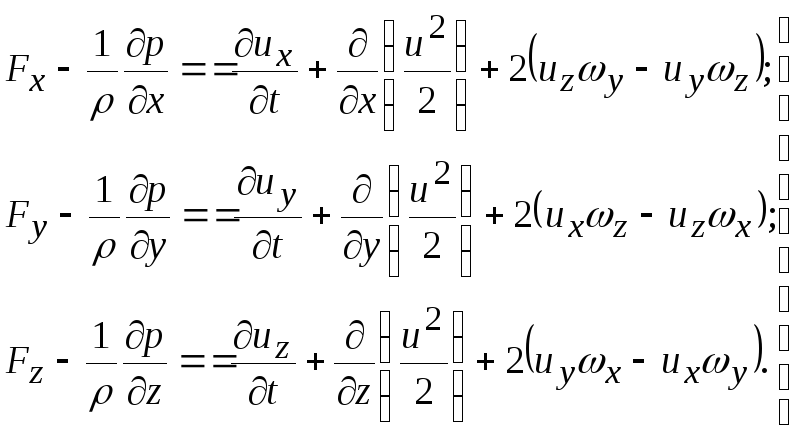 (4.5)4.4. Уравнения громеки при действии массовых сил, имеющих потенциал Если действующие на жидкость массовые силы обладают потенциалом, то проекции плотности распределения массовых сил  представляются частными производными от потенциальной функции : откуда  (4.5a)Подставив значения 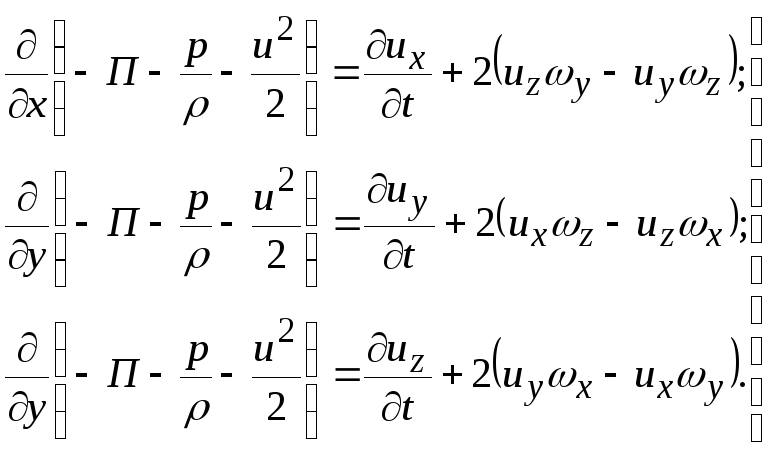в систему (4.5), получим уравнения движения несжимаемой жидкости под действием сил, имеющих потенциал: (4.6)4.5. Уравнение бернулли для установившегося ДВИЖЕНИЯ НЕВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ ПРИ ДЕЙСТВИИ МАССОВЫХ СИЛ, ИМЕЮЩИХ ПОТЕНЦИАЛ При установившемся движении частные производные составляющих скорости по времени равны нулю:  Тогда для рассматриваемого установившегося движения невязкой жидкости уравнения (4 б) принимают вид 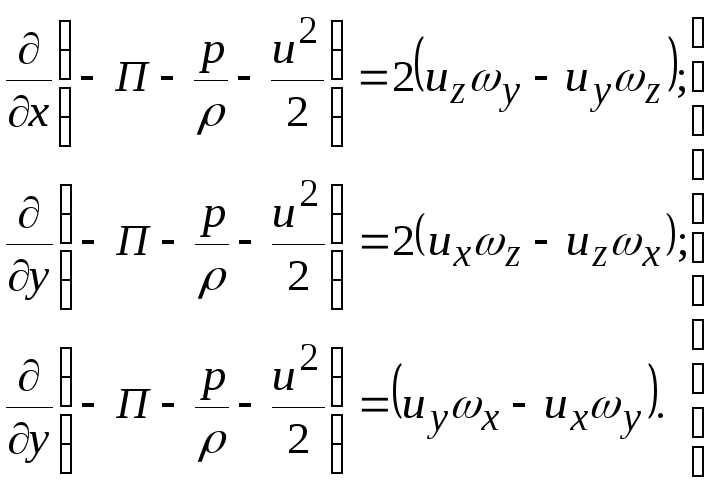 (4 7)Выбрав на любой линии тока элементарное перемещение  , получим для его проекций на координатные оси .Умножив каждое из уравнений (4.6) последовательно на проекции элементарного перемещения вдоль линии тока и просуммировав уравнения, получим   .Правую часть полученного выражения можно переписать в виде определителя. Тогда 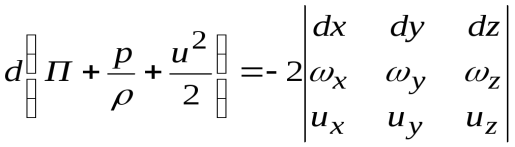 . (4.8)Если определитель обращается в нуль, то  и  . (4.9)Уравнение (4.9) называется уравнением Бернулли по имени действительного члена Петербургской Академии наук Даниила Бернулли. Впервые термин «гидродинамика» появился в книге Д. Бернулли опубликованной в 1738 г. Выясним, в каких случаях установившегося движения невязкой несжимаемой жидкости справедливо уравнение Бернулли или, иначе говоря, в каких случаях определитель в правой части уравнения (4.8) обращается в нуль. Известно, что определитель равен нулю, если две строки (или два столбца) равны или пропорциональны друг другу или если одна из его строк или один из столбцов равны нулю. Рассмотрим эти случаи последовательно. 1. Пропорциональны члены первой и третьей строк, т.е. уравнение Бернулли справедливо при выполнении условия  .Это условие выполняется на линиях тока (3.7). Таким образом, уравнение Бернулли справедливо вдоль линий тока. Для различных линий тока значение постоянной уравнения (4.9) в общем случае будет различным. 2. Пропорциональны члены первой и второй строк, т. е. уравнение Бернулли справедливо при выполнении условия  .Это условие выполняется на вихревых линиях (3.12). Поэтому уравнение Бернулли справедливо вдоль вихревых линий. На каждой вихревой линии константа уравнения (4.9) сохраняет свое значение и может изменяться при переходе с одной линии на другую. 3. Пропорциональны члены второй и третьей строк:  . (4.10)Тогда    .Подставив полученные выражения в уравнение вихревой линии  получим уравнение линий тока  Таким образом, в рассматриваемом случае векторы скорости  и угловой скорости параллельны (их направления совпадают). Такое движение называется винтовым. Частицы при винтовом движении перемещаются по линиям тока (так как движение установившееся, то линии тока и траектории частиц совпадают), а линии тока в то же время являются вихревыми линиями, т. е. частицы еще и вращаются вокруг линии тока.Из условий (4.10) видно, что равенство определителя нулю в этом случае не зависит от координат. Соответственно постоянство удельной энергии при винтовом движении обеспечивается во всем пространстве, занятом находящейся в винтовом движении жидкостью. Уравнение Бернулли (4.9)  при винтовом движении применимо к любой точке жидкости. 4. Условие равенства нулю членов второй строки определителя  означает, что движение безвихревое (потенциальное). Уравнение Бернулли (4.9) действительно для всех точек области потенциального движения. 5. Условие равенства нулю членов третьей строки определителя  соответствует равновесию жидкости. Основы теории колебаний 10. Критические состояния ротора с анизотропными опорами: расчетная схема, уравнения движения и их решение, анализ решения. ГЛЕБОВ ОТВЕТ 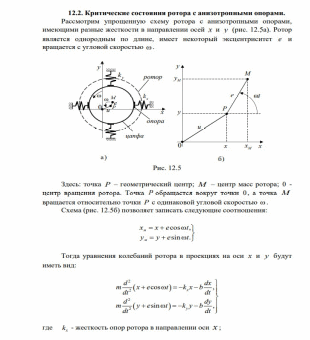  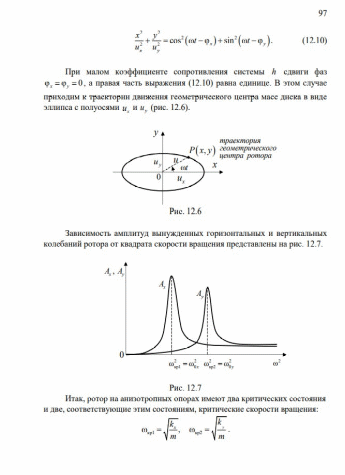 ОУМ №2 – «Прочность и надежность энергоустановок» Строительная механика энергоустановок 1. Задачи прочностного анализа и методы исследования. Классификация сил, расчетных схем и задач строительной механики. ГЛЕБОВ ОТВЕТ  Дополнительная информация Строительная механика – это наука о принципах и методах определения НДС инженерных конструкций, анализа их устойчивости и динамического поведения. Сопротивление материалов – наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и машин. Строительная механика – наука, занимающаяся расчетом инженерных сооружений на прочность, устойчивость и жесткость. В отличие от сопротивления материалов, строительная механика рассматривает не отдельный элемент (стержень, балку, вал и т.д.), а систему элементов в целом. Прочность – способность конструкции, ее частей и деталей выдерживать определенную нагрузку, не разрушаясь. Расчет на прочность служит для определения минимально необходимых размеров элементов конструкций, исключающих возможность разрушения под действием нагрузок. Жесткость – способность конструкции и ее элементов противостоять внешним нагрузкам в отношении деформации (изменения формы и размеров). Расчет на жесткость связан с определением деформаций и перемещений, возникающих в элементах конструкций. Жесткость считают обеспеченной, если упругие перемещения не превосходят заданных величин, допустимых при эксплуатации конструкции. Устойчивость – способность конструкции и ее элементов сохранять определенную начальную форму упругого равновесия. В настоящее время значительная часть курса строительной механики посвящена расчету стержневых систем. Строительная механика ЭУ – область строительной механики сооружений, в которой в качестве объекта исследования рассматриваются конструкции отдельных агрегатов и частей ЭУ или конструкция ЭУ в целом. В настоящее время значительная часть курса строительной механики посвящена расчету стержневых систем. Методыисследования аналитические; использованиеинженерных методик; использованиечисленных методоврасчета(МКЭ,МГЭ,МКРи т.д.); использованиесистеминженерныхрасчетов(CAE-системы–ComputerAided Engineering)–ANSYS,ABAQUS,NASTRAN,SolidWorksSimulationит.д.; экспериментальные методы исследования. Классификациясил Похарактерудействия сосредоточенные; поверхностные; массовые. Поскоростиизменения статические; Динамические Циклические нагрузки Температурные нагрузки Классификациязадач Взависимостиотмерностирешаемойзадачи нульмерные; одномерные; плоские (ПНС, ПДС); осесимметричные; трехмерные. Взависимостиотучетаилинеучетанелинейностей линейные; нелинейные. Взависимостиотскоростиизменениянагрузки статические (стационарные); квазистационарные; динамические. Теоретические основы вибродиагностики 1. Вибрации в технике, как основной показатель работоспособности агрегатов, машин, установок. ГЛЕБОВ ОТВЕТ ОУМ №3 – «Энергетические машины и установки» Конструкция и проектирование турбомашин 13. Основные показатели работы КС ГЛЕБОВ Тепловая мощность камеры  (кВт) выражается количеством тепла, которое выделяется в единицу времени при полном сгорания топлива [5]: , (1.1)где В - расход сжигаемого топлива, кг/с;  - низшая теплота сгорания топлива, кДж/кг.Объемная теплонапряженность q (кВт/м3) характеризует компактность, а значит, и эффективность использования объема: 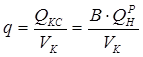 , (1.2)где  - объем камеры сгорания, м3 (принимается обычно равным объему пламенной (жаровой) трубы).С повышением давления в камере мощность и теплонапряженность её увеличиваются, так как при этом возрастает массовый расход воздуха через камеру, а, следовательно, и расход сжигаемого топлива. Поэтому при оценке камер сгорания их объемную теплонапряженность обычно берут относительно к давлению в камере, т.е.: 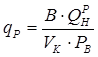 , (1.3)где  - давление на входе в камеру, МПа.Потери энергия в камере сгорания состоят из тепловых потерь и потерь давления. Тепловой к. п. д. камеры сгорания учитывает все тепловые потери: 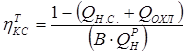 , (1.4)где  - потери теплоты от неполного сгорания топлива (химический и физический недожог). У современных камер сгорания эти потери не должны превышать 1-5 % общего расхода теплоты при работе на всем диапазоне рабочих нагрузок и 1-3 % при работе на расчетной нагрузке; - потери за счет отдачи теплоты, в окружающее пространство нагретой поверхностью камеры и примыкающих к ней трубопроводов. Эти потери обычно бывают не более 0,5 % расхода теплоты.В существующих камерах сгорания тепловой к. п. д., при работе на расчетном режиме:  Полные потери давления в камере сгорания складываются из гидравлических потерь и дополнительных. Гидравлические потери возникают без подвода теплоты к камере, в результате потерь на трения при прохождении газового потока и местных сопротивлений от воздухо-направляющих ребер, завихрителей и т.д. Эти потери определяются при холодной продувке камеры. Дополнительные потери давления вызваны нагревом газа при сгорании топлива в камере. Плотность газа в этом случае уменьшается, а скорость газового потока увеличивается. Процесс снижения давления в газовом потоке при подводе теплоты подробно рассматривается в курсе газовой динамики. Полные потери давления принято выражать в долях или процентах по отношению к давлению полного торможения воздуха на входе в камеру: 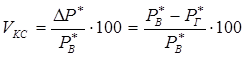 , (1.5)где  - полная потеря давления в камере; - давление полного торможения газов на выходе из камеры.Давление полного торможения воздуха в газе: 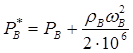 ,  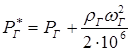, (1.6)где  - статическое давление воздуха на входе и газа на выходе, МПа; rВ rГ - плотность воздуха и газа, кг/м3; wВ wГ - средние скорости воздуха во входном сечении и газа в выходном сечения камеры, м/с.В современных конструкциях камер сгорания полные потери давления обычно бывают в пределах  = 1-3 %.Потери давления в камере сгорания снижают к. п. д. ГТУ. Это можно учесть с помощью аэродинамического к. п. д. камеры сгорания  , который обычно составляет:  . Общий к. п. д. камеры сгорания можно выразить в виде произведения: . (1.7)У современных камер сгорания  .Общий коэффициент избытка воздуха в камере сгорания: 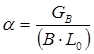 , (1.8)где  и  - соответственно расход воздуха и топлива в камере, кг/с; - теоретически необходимое количество воздуха для сжигания 1 кг топлива рассчитывается элементарному составу топлива.Как уже отмечалось в современных ГТУ a = 4-8. Непосредственно в процессе сгорания участвует не все количество воздуха GB, а только часть его - первичный воздух, поступающий в зону горения:  , (1.9)где a1 - коэффициент избытка первичного воздуха, зависящий от конструкции камеры сгорания и вида сжигавшего топлива. Обычно  ОУМ №4 – «Проектирование и управление систем ГПА и ЭУ» Конструкция и проектирование систем газоперекачивающих агрегатов и энергоустановок 5. Рабочий процесс в ступени центробежного нагнетателя. ГЛЕБОВ ОТВЕТ Рабочий процесс в ступени центробежного компрессора. 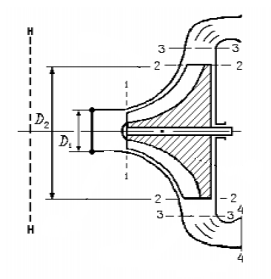 Рисунок 5. Характерные сечения ступени центробежного компрессора. Для более подробного пояснения принципа действия ступени центробежного компрессора рассмотрим движение газа в его элементах. Обозначим характерные сечения ступени центробежного компрессора (см. рисунок 5). Н—Н — сечениена входе в центробежную машину. Параметры газа в этом сечении: давление Рн, температура Тн и скорость Сн ; 1—1 —сечение на входе в рабочее колесо. Параметры газа в этом сечении: давление Р1, температура Т1 и скорость С1; 2—2 — выход из рабочего колеса. Параметры газа в этом сечении: давление Р2, температура Т2 и скорость С2; 3—3 — выход из диффузора. Параметры газа в этом сечении: давление Р3, температура Т3 и скорость С3; 4—4 — сечение на выходе из компрессора. Параметры газа в этом сечении: давление Р4, температура Т4 и скорость С4. Рассмотрим процесс течения газа вдоль цилиндрической поверхности А-А (см. рисунок 6). 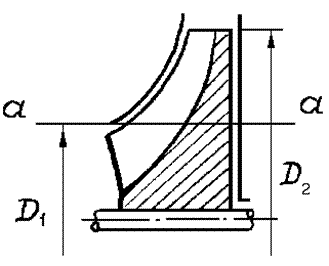 Рисунок 6. Схема ступени центробежного компрессора Для этого рассечем ступень центробежного компрессора цилиндрической поверхностью диаметром D1, ось которой совпадает с осью колеса. Развернув эту поверхность на плоскость, получим плоскостное сечение. Плоскостное сечение рабочего колеса представлено на рисунке 7. Колесо вращается с угловой скоростью ω (радиан /сек) :  ,где n — число оборотов колеса, мин-1 и окружной скоростью U (м / сек) на диаметре D1:  .Газ поступает на вход в рабочее колесо с абсолютной скоростью С1. Струйки газа подхватываются лопатками колеса и начинают вращаться вместе с колесом с окружной (переносной) скоростью U1. В результате поток движется в межлопаточных каналах колеса со скоростью W1 называемой относительной скоростью и равной геометрической разности абсолютной C1 и окружной U1 скоростей: W1= C1 – U1 . Относительной скоростью W1 называют скорость потока газа, измеренную в неподвижной относительно межлопаточного канала системе координат, одна из осей которой совпадает с направлением движения потока. В соответствии с данным уравнением по правилу сложения векторов строится параллелограмм скоростей на входе газа в рабочее колесо (см. рисунок 8). В теории лопаточных машин вместо параллелограмма скоростей принято использовать треугольник скоростей (см. рисунок 7, 8). 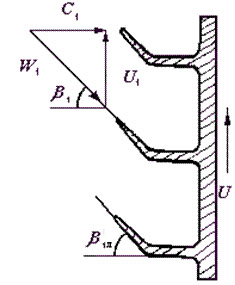 Рисунок 7. Плоскостное сечение рабочего колеса центробежного компрессора. 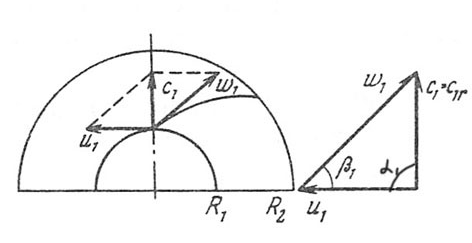 Рисунок 8. Параллелограмм и треугольник скоростей при радиальном (безударном) входе газа в рабочее колесо. С целью обеспечения безударного входа потока в рабочее колесо необходимо, чтобы вектор относительной скорости W1 совпадал с направлением передних кромок лопаток рабочего колеса, т. е. должно соблюдаться равенство:  где β1 – угол между вектором окружной скорости U1 и вектором относительной скорости W1 ; β1л – конструкторский угол установки лопаток на диске на входе в рабочее колесо. Разница между углами β1 и β1л называется углом атаки i. i = βл - β1л На расчетном режиме i ≈ 0. Угол α между вектором окружной скорости U1 и вектором абсолютной скорости С1 называется расчетный (рабочий угол). При осесимметричном входе газа в ступень α1 = 900. При отклонении от расчетного режима работы центробежного компрессора угол β1 изменяется (см. рисунок 9). Увеличение или уменьшение расхода газа через ступень приводит к соответствующему изменению абсолютной скорости C1, а окружная скорость U1 сохраняется неизменной (угол сохраняется α1=900, так как поток в рабочее колесо входит осесимметрично). Следовательно, вектор относительной скорости W1 изменяется по величине и направлению, изменяется угол β1. При этом угол атаки i может принять как отрицательное значение (недогруженный режим при угле β1 //), так и положительное значение (перегруженный режим при угле β1 /). 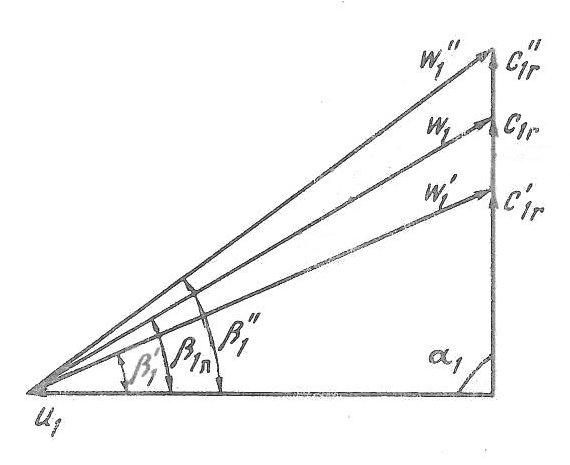 Рисунок 9. Изменение треугольника скоростей на входе газа в рабочее колеса при отклонении от расчетного режима работы При движении в межлопаточном канале рабочего колеса струйки газа под действием центробежных сил стремятся сохранить радиальное движение вдоль канала. Кроме того, струйки газа подвергаются силовому воздействию от лопаток рабочего колеса, вращающегося с окружной скоростью U. В результате на выходе из канала струйки газа покидают рабочее колесо с абсолютной скоростью C2, которая складывается из окружной (переносной) скорости U2, направленной по касательной к окружности колеса, и относительной скорости W2, отклоненной от радиального направления (на угол 90- β2) из-за неравномерности распределения давлений и скоростей внутри канала (см. рисунок 10). 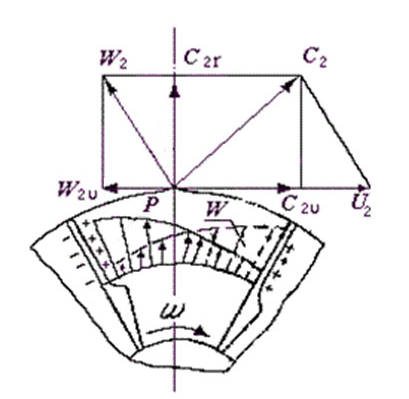 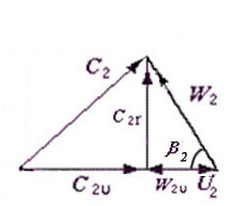 Рисунок 10. Параллелограмм и треугольник скоростей на выходе газа из рабочего колеса и эпюры распределения давлений Р и относительной скорости W в межлопаточном канале. Эпюры распределения давлений Р и относительной скорости W в межлопаточном канале приведены на рисунке 10. На стороне лопатки, направленной в сторону вращения, давление больше (знак «+»), чем на противоположной стороне (знак «—»). Там, где больше давление, меньше скорость и наоборот. В результате неравномерности распределения скоростей в межлопаточном канале струйка газа как бы перемещается против вращения рабочего колеса (проскальзывает относительно диска) со скоростью W2U (окружная составляющая относительной скорости W2). Величина W2U зависит от числа лопаток ZК на рабочем колесе. Скорость W2U тем меньше, чем больше число лопаток ZК (при увеличении количества лопаток снижается неравномерность распределения давлений и скоростей внутри канала). Угол между вектором окружной скорости U2 и вектором относительной скорости W2 равен β2. Согласно законам газовой динамики, при течении газа в длинных каналах происходит упорядочение потока. Поэтому в межлопаточном канале рабочего колеса на некотором расстоянии от входа поток начинает течь параллельно стенкам канала, т.е. на выходе из рабочего колеса угол β2 будет равен конструкторскому углу установки лопаток β2л (в том числе и при отклонении от расчетного режима работы). Из параллелограмма и треугольника скоростей (см. рисунок 9) видно, что окружная составляющая абсолютной скорости С2U определяется как геометрическая разность окружной (переносной) скорости U2 и окружной составляющей относительной скорости W2U : С2U =U2 — W2U Скорость С2U характеризует величину закрутки, полученной потоком в рабочем колесе, а радиальная составляющая абсолютной скорости С2r определяет величину расхода газа через рабочее колесо. Выгодно, чтобы при заданных окружной скорости U2 и абсолютной скорости С2, величина С2г, была как можно большей. Максимальная величина С2r будет при бесконечно большом числе лопатокZK,так как при этом не будет отклонения относительной скорости от радиального направления, т. е. W2U = 0, а C2U = U2. В реальных условиях применять такое рабочее колесо невозможно, так как в этом случае межлопаточные каналы будут очень узкие, и вследствие вязкости газа, в них будет значительное газодинамическое трение и потери энергии. Поэтому на практике используют центробежные нагнетатели с конечным числом лопаток ZK = 18…40. Оптимальное конечное количества лопаток может быть произведено по формуле: ZK = β2л /3 + (3…5), где β2л – конструкторский угол установки лопаток на диске на выходе из рабочего колеса. Величина закрутки потока газа на выходе из рабочего колеса оценивается коэффициентом закрутки (циркуляции) μ, равном: μ =  При Zк → ∞ значение коэффициента μ = 1. У существующих центробежных компрессоров и нагнетателей при числе лопаток на рабочем колесе Zк = 18…40 коэффициент закрутки составляет μ = 0,9…0,95. При отклонении от расчетного режима работы изменяется величина радиальной составляющей абсолютной скорости С2r и величина окружной (переносной) скорости U2. Соответственно, изменяется направление и величина вектора абсолютной скорости С2. Треугольник скоростей на выходе газа из рабочего колеса представлен на рисунке 11. 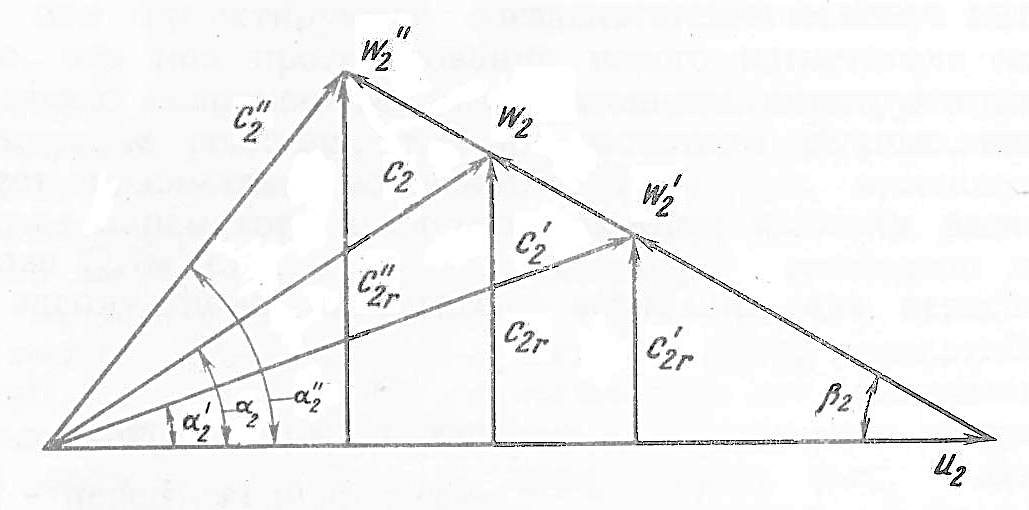 Рисунок 11. Изменение треугольника скоростей на выходе газа из рабочего колеса при отклонении от расчетного режима работы В результате поток из рабочего колеса (вектор абсолютной скорости С2) входит в диффузорную систему (лопаточный и безлопаточный диффузоры) под нерасчетным рабочим углом α2 / или α2 //. На входе в лопаточный диффузор образуются ударные течения газа, что вызывает потери энергии. Как отмечалось ранее, в диффузорной системе происходит снижение скорости и повышение статического давления. Снижение абсолютной скорости в диффузоре определяется отношением входной и выходной площадей:  ,где С2 и С3 — скорости на входе и выходе из диффузора; F2 и F3 — площади на входе и выходе из диффузора. При постоянной по радиусу ширине щели отношение площадей равно отношению диаметров:  .В безлопаточном диффузоре отношение диаметров на выходе и входе обычно составляет:  = 1,65 …2.В лопаточном диффузоре отношение диаметров на выходе и входе обычно составляет: = 1,25…1,35 .Автоматическое регулирование энергоустановок Причины возникновения и виды прецессии ротора. ГЛЕБОВ ОТВЕТ |