Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
2.3. Элементы процесса измеренийИзмерение — сложный процесс, включающий в себя взаимодействие целого ряда его структурных элементов. К ним относятся: измерительная задача, объект измерения, принцип, метод и средство измерения и его модель, условия измерения, субъект измерения, результат и погрешность измерения. Эти элементы и их взаимосвязи показаны на рис. 2.5 в виде структурной схемы. Из нее видно, что процесс измерения протекает по двум параллельным ветвям, содержащим соответствующие друг другу элементы, относящиеся к реальности (верхняя ветвь) и ее отражению, или познанию (нижняя ветвь). Элементы обеих ветвей, неразрывно связанных между собой, соответствуют друг другу по типу "реальность — отражение (модель)". Первым начальным элементом каждого измерения является его задача (цель). Задача любого измерения заключается в определении значения выбранной (измеряемой) ФВ с требуемой точностью в заданных условиях. Постановку задачи измерения осуществляет субъект измерения — человек. При постановке задачи конкретизируется объект измерения, в нем выделяется измеряемая ФВ и определяется (задается) требуемая погрешность измерения. Объект измерения — это реальный физический объект, свойства которого характеризуются одной или несколькими измеряемыми ФВ. Он обладает многими свойствами (Св1 ..., Свi, см. рис. 2.5) и находится в многосторонних и сложных связях с другими объектами. Субъ ект измерения — человек принципиально не в состоянии представить себе объект целиком, во всем многообразии его свойств и связей. Вследствие этого взаимодействие субъекта с объектом возможно только на основе математической модели объекта. 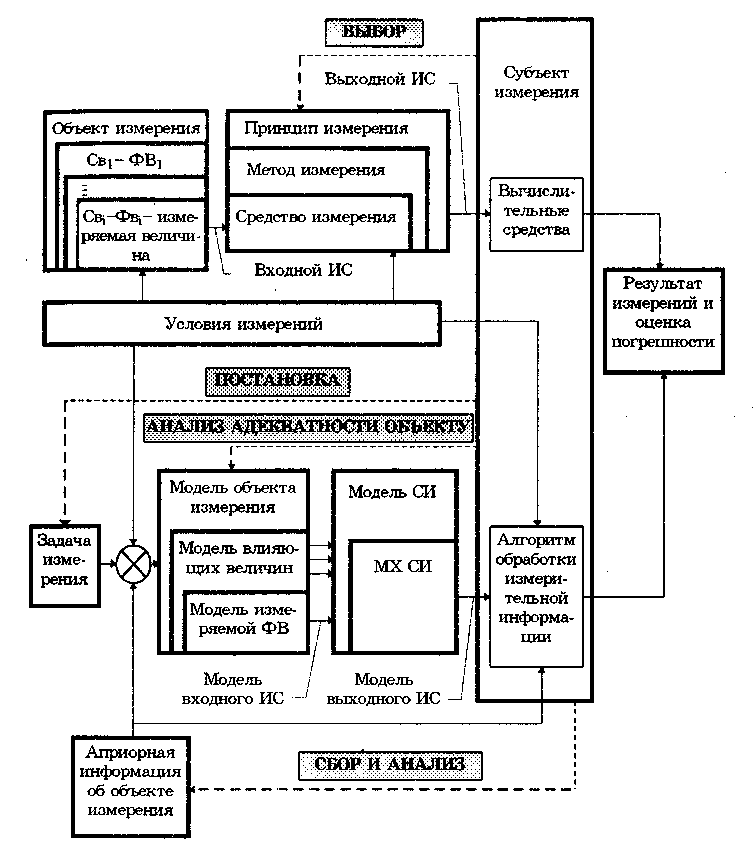 Рис. 2.5. Основные элементы процесса измерения: СИ — средство измерений, MX — метрологические характеристики, ИС — измерительный сигнал, ФВ — физическая величина, Св — свойство Математическая модель объекта измерения — это совокупность математических символов (образов) и отношений между ними, которая адекватно описывает интересующие субъекта свойства объекта измерения. Модель объекта измерения строится до выполнения измерения в соответствии с решаемой задачей на основе априорной информации об объекте и условиях измерения. На рис. 2.5 это отражено в виде суммирования сведений о цели, условиях измерения и априорной информации об объекте. Модель объекта измерения должна удовлетворять следующим требованиям: • погрешность, обусловленная несоответствием модели объекту измерения, не должна превышать 10% предельно допускаемой погрешности измерения; • составляющая погрешности измерения, обусловленная нестабильностью измеряемой ФВ в течение времени, необходимого для проведения измерения, не должна превышать 10% предельно допускаемой погрешности. Если выбранная модель не удовлетворяет этим требованиям, то следует перейти к другой модели объекта измерений. Априорная информация, т.е. информация об объекте измерения, известная до проведения измерения, является важнейшим фактором, обуславливающим его эффективность. При полном отсутствии этой информации измерение в принципе невозможно, так как неизвестно, что же необходимо измерить, а следовательно, нельзя выбрать нужные средства измерений. При наличии априорной информации об объекте в полном объеме, т.е. при известном значении измеряемой величины, измерения попросту не нужны. Указанная информация определяет достижимую точность измерений и их эффективность. Измеряемая величина определяется как параметр принятой модели, а ее значение, которое можно было бы получить в результате абсолютно точного эксперимента, принимается в качестве истинного значения данной величины. Идеализация, принятая при построении модели объекта измерения, обуславливает несоответствие параметра модели исследуемому свойству объекта. Это несоответствие называют пороговым.. Обычно на практике из-за трудности оценивания пороговое несоответствие стремятся сделать пренебрежимо малым. ^ Цель построения модели объекта измерения состоит в выявлении (представлении) конкретной ФВ, подлежащей определению. Собственно следует говорить не о модели объекта измерения в делом, а о модели его измеряемого свойства или измеряемой ФВ. Модель объекта измерения необязательно должна быть математической. Ее характер должен определяться видом и свойствами объекта измерений, а также целью измерений. Моделью может служить любое приближенное описание объекта, которое позволяет выделить параметр модели (или функционал параметров), являющийся измеряемой величиной и отражающий то свойство объекта измерений, которое необходимо оценить для решения измерительной задачи. Модель должна достаточно хорошо отражать две группы свойств (ФВ) объекта измерений: определяемые при измерении и влияющие на результат измерения. Основной проблемой моделирования объектов измерений является выбор таких моделей, которые можно считать адекватно описывающими измеряемые величины (свойства) данного объекта. Важно отметить, что адекватность модели обуславливается не только теми свойствами объекта, которые требуется определить в рамках данной измерительной задачи, но и теми, которые могут влиять на результаты измерения искомой величины. Построение адекватных моделей объектов измерений до настоящего времени является сложной творческой и неформализуемой задачей. Ее решение требует высокой квалификации, опыта и, естественно, инженерной интуиции. При этом зачастую приходится решать две взаимоисключающие задачи: модель должна адекватно отражать все свойства объекта, необходимые для решения измерительной задачи, и в то же время быть по возможности простой и содержать минимум параметров. В большинстве практических инженерных задач модели объектов намерений достаточно очевидны и, как правило, несложны. Объект измерения характеризуется набором свойств и описывающих их ФВ. На рис. 2.5 одна из них (i-я) является измеряемой величиной. Измеряемая величина — это ФВ, подлежащая определению в соответствии с измерительной задачей. До недавнего времени понятие "физическая величина" считалось достаточным для постановки и решения всех измерительных задач. Однако из-за существенного расширения области применения измерений, усложнения их задач и усиления требований к точности и достоверности в ряде случаев оно перестало удовлетворять потребности в экспериментальном определении различных свойств разнообразных объектов. При планировании современных измерений требуется введение более конкретных понятий, определяемых целями измерений, чем весьма общего понятия "физическая величина". В настоящее время под измеряемой величиной понимается параметр или функционал параметра модели объекта измерений, отражающий то его свойство, количественную оценку которого необходимо получить в результате измерений. Измеряемая величина всегда имеет размерность определенной ФВ, но представляет собой некоторую ее конкретизацию, обусловленную свойствами объекта измерений, которые связаны с поставленной целью измерений. Для иллюстрации вышесказанного рассмотрим ряд примеров. Пример 2.2. Объект измерения — поршень грузопоршневого манометра. Цель измерения — определение эффективной площади поршня. Априорная информация состоит в том, что поперечное сечение поршня незначительно отличается от круга. В соответствии с этой информацией в качестве модели поршня принимается прямой цилиндр, поперечное сечение которого близко к кругу. Эффективную площадь поршня в некоторых случаях определяют по среднему диаметру его поперечного сечения. В соответствии с целью измерения в качестве параметра модели — измеряемой величины — принимается средний диаметр поперечного сечения поршня. Значение измеряемой величины в этом случае можно выразит функционалом вида где d(ai) — диаметр, имеющий угловую координату аi = 30(i-1), т.е. функцию аргумента аi, выраженную в градусах. Пример 2.3. Объект измерения — переменное напряжение. Цель измерения — оценка мощности, которая может быть выделена в нагрузку. До проведения измерений (априорная информация) известно, что переменное напряжение является периодическим и имеет форму, близкую к синусоидальной. В связи с этим в качестве модели принимается функция синуса, а качестве параметра — измеряемой величины — его среднее квадратическое значение, определяемое по формуле 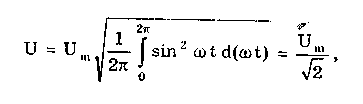 где Um и — амплитуда и круговая частота синусоидального напряжения соответственно. Если априорная информация о форме напряжения отсутствует, то моделью напряжения может быть, например, произвольная периодическая функция u(t). Тогда значение измеряемой величины должно быть выражено функционалом вида где Т — период функции. Измерительная информация, т.е. информация о значениях измеряемой ФВ, содержится в измерительном сигнале. Измерительный сигнал — это сигнал, содержащий количественную информацию об измеряемой ФВ. Он поступает на вход СИ, при помощи которого преобразуется в выходной сигнал, имеющий форму, удобную либо для непосредственного восприятия человеком (субъектом измерения), либо для последующей обработки и передачи. Субъект измерения осуществляет выбор принципа, метода и средства измерений. Принцип измерений — совокупность физических принципов, на которых основаны измерения, например применение эффекта Джозефсона для измерения электрического напряжения или эффекта Доплера для измерения скорости. Метод измерения — это прием или совокупность приемов сравнения измеряемой ФВ с ее единицей в соответствии с реализованным принципом измерения. Метод измерения должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу их в разряд случайных. Методы измерения можно классифицировать по различным признакам. Известна [13] классификация по основным измерительным операциям. Она тесно связана с элементарными СИ, реализующими эти операции. Данная классификация ориентирована на структурное описание средств измерений и поэтому важна для измерительной техники, а также метрологии информационно-измерительных систем. Для метрологического анализа более важными являются традиционные классификации, основанные на следующих признаках. Первый из них — физический принцип, положенный в основу измерения. По нему все методы измерений делятся на электрические, магнитные, акустические, оптические, механические и т.д. В качестве второго признака классификации используется режим взаимодействия средства и объекта измерений. В этом случае все методы измерений подразделяются на статические и динамические. Третьим признаком может служить применяемый в СИ вид измерительных сигналов. В соответствии с ним методы делятся на аналоговые и цифровые. Наиболее разработанной является классификация по совокупности приемов использования принципов и средств измерений. По этой классификации различают метод непосредственной оценки и методы, сравнения (рис. 2.6). Эти устоявшиеся в литературе названия, как справедливо отмечено в [24], не совсем удачны, поскольку наводят на мысль о возможности измерения без сравнения. Представляется [24] более правильным говорить о опосредованном и непосредственном сравнении с мерой. При этом непосредственным и опосредованным сравнение может быть как во времени, так и в отношении физической природы измеряемых величин.  Рис. 2.6. Классификация методов измерения Сущность метода непосредственной оценки состоит в том, что о значении измеряемой величины судят по показанию одного (прямые измерения) или нескольких (косвенные измерения) средств измерений, которые заранее проградуированы в единицах измеряемой величины или единицах других величин, от которых она зависит. Это наиболее распространенный метод измерения. Его реализуют большинство средств измерений. Простейшими примерами метода непосредственной оценки могут служить измерения напряжения электромеханическим вольтметром магнитоэлектрической системы или частоты импульсной последовательности методом дискретного счета, реализованным в электронно-счетном частотомере. Другую группу образуют методы сравнения: дифференциальный, нулевой, совпадений, замещения. К ним относятся все те методы, при которых измеряемая величина сравнивается с величиной, воспроизводимой мерой. Следовательно, отличительной особенностью этих методов сравнения является непосредственное участие мер в процессе измерения. При дифференциальном методе измеряемая величина X сравнивается непосредственно или косвенно с величиной Xм, воспроизводимой мерой. О значении величины X судят по измеряемой прибором разности Х = X – Xм и по известной величине Хм, воспроизводимой мерой. Следовательно, Х = Хм+ Х. При дифференциальном методе производится неполное уравновешивание измеряемой величины. Он сочетает в себе часть признаков метода непосредственной оценки и может дать весьма точный результат измерения, если только измеряемая величина и величина, воспроизводимая мерой, мало отличаются друг от друга. Например, если разность этих двух величин составляет 1% и измеряется с погрешностью до 1%, то тем самым погрешность измерения искомой величины уменьшается до 0,01% (если не учитывать погрешность меры). Примером дифференциального метода может служить измерение вольтметром разности двух напряжений, из которых одно известно с большой точностью, а другое представляет собой искомую величину. Нулевой метод является разновидностью дифференциального метода. Его отличие состоит в том, что результирующий эффект сравнения двух величин доводится до нуля. Это контролируется специальным измерительным прибором высокой точности — нуль-индикатором. В данном случае значение измеряемой величины равно значению, которое воспроизводит мера. Высокая чувствительность нуль-индикаторов, а также выполнение меры с высокой точностью позволяют получить малую погрешность измерения. Пример нулевого метола — взвешивание на весах, когда на одном плече находится взвешиваемый груз, а на другом — набор эталонных грузов. Другой пример — измерение сопротивления с помощью уравновешенного моста. Метод замещения заключается в поочередном измерении прибором искомой величины и выходного сигнала меры, однородного с измеряемой величиной. По результатам этих измерений вычисляется искомая величина. Поскольку оба измерения производятся одним и тем же прибором в одинаковых внешних условиях, а искомая величина определяется по отношению показаний прибора, погрешность результата измерения уменьшается в значительной мере. Так как погрешность прибора неодинакова в различных точках шкалы, наибольшая точность измерения получается при одинаковых показаниях прибора. Пример метода замещения — измерение большого электрического активного сопротивления путем поочередного измерения силы тока, протекающего через контролируемый и образцовый резисторы. Питание цепи при измерениях должно осуществляться от одного и того же источника постоянного тока. Выходное сопротивление источника тока и измерительного прибора — амперметра должно быть очень мало по сравнению с измеряемыми сопротивлениями. При методе совпадений разность между измеряемой величиной и величиной, воспроизводимой мерой, определяют, используя совпадение отметок шкал или периодических сигналов. Этот метод широко используется в практике неэлектрических измерений. Примером может служить измерение длины при помощи штангенциркуля с нониусом. Примером использования данного метода в электрических измерениях является измерение частоты вращения тела посредством стробоскопа. Метод измерений реализуется в средстве измерений — техническом средстве, используемом при измерениях и имеющем нормированные метрологические свойства (ГОСТ 16263-70). Такое определение представляется не совсем удачным. По сути дела, под СИ следует понимать техническое средство, предназначенное для измерений и позволяющее решать измерительную задачу путем сравнения измеряемой величины с единицей или шкалой ФВ [24]. Средство измерений является обобщенным понятием, объединяющим самые разнообразные конструктивно законченные устройства, которые обладают одним из двух признаков: • вырабатывают сигнал (показание), несущий информацию о размере(значении) измеряемой величины; • воспроизводят величину заданного (известного) размера. Объединение технических средств по этим двум признакам сделано только из соображений целесообразности общего метрологического анализа, удобства изложения и регламентации метрологических требований и правил, единых для всех видов СИ. При использовании СИ весьма важно знать степень соответст- f вия выходной измерительной информации истинному значению определяемой величины. Для ее установления введено правило, по которому требуется нормировать метрологические характеристики всех средств измерений. Метрологические характеристики — это характеристики свойств СИ, которые оказывают влияние на результат измерений и его погрешности и предназначены для оценки технического уровня и качества СИ, а также определения результатов измерений и расчетной оценки характеристик инструментальной составляющей погрешности измерений. Средство измерений входит в обе ветви структуры измерения (см. рис. 2.5). В реальности оно взаимодействует с объектом измерений, в результате чего появляется входной (для СИ) сигнал и отклик на него — выходной сигнал, подлежащий обработке с целью нахождения результата измерения и оценки его погрешности. В области отражений СИ описывается моделью, необходимой для эффективной обработки опытных данных. Эта модель представлена совокупностью его метрологических характеристик. Средства измерений могут быть элементарными (меры, устройства сравнения и измерительные преобразователи) и комплексными (регистрирующие и показывающие измерительные приборы, системы, измерительно-вычислительные комплексы). Детально СИ рассматриваются в гл. 11. В процессе измерения важную роль играют условия измерения — совокупность влияющих величин, описывающих состояние окружающей среды и средства измерений. Влияющая величина — это физическая величина, не измеряемая данным СИ, но оказывающая влияние на его результаты. Изменение условий измерения приводит к изменению состояния объекта измерения. Это в свою очередь определяет влияние условий измерения на выделенную ФВ и через нее — на измеряемую величину и отклонение значения действительной величины от той, что была определена при формировании измерительной задачи. Влияние условий измерения на СИ проявляется в изменении его метрологических характеристик. При этом та часть погрешности измерения, которая возникает из-за изменения условий, называется дополнительной погрешностью. В соответствии с установленными для конкретных ситуаций диапазонами значений влияющих величин различают нормальные, рабочие и предельные условия измерений. Нормальные условия измерений, — это условия, при которых влияющие величины имеют нормальные или находящиеся в пределах нормальной области значения. Нормальная область значений влияющей величины — это область значений, в пределах которой изменением результата измерений под воздействием влияющей величины можно пренебречь в соответствии с установленными нормами точности. Нормальные условия измерений задаются в нормативно-технической документации на СИ. При нормальных условиях определяется основная погрешность данного СИ. В табл. 2.1 приведены номинальные значения ряда влияющих ФВ при нормальных условиях. Рабочими называются условия измерений, при которых влияющие величины находятся в пределах своих рабочих областей. Рабочая область значений влияющей величины — это область, в пределах которой нормируется дополнительная погрешность или изменение показаний СИ. Предельные условия измерений — это условия, характеризуемые экстремальными значениями измеряемой и влияющих величин, которые СИ может выдержать без разрушений и ухудшения его метрологических характеристик. Конечной целью любого измерения является его результат — значение ФВ, полученное путем ее измерения. Результат измерения представляется именованным или неименованным числом. Совместно с результатом измерений при необходимости приводят данные об условиях измерений. При использовании термина "результат измерения" следует четко указать, к чему он относится: показанию СИ, исправленному или не исправленному результату, и проводилось ли усреднение результатов нескольких измерений. Следует отметить, что исправленным результатом измерений называется полученное с помощью СИ значение величины и уточненное путем введения в него необходимых поправок на действие предполагаемых систематических погрешностей. Таблица 2.1 Номинальные значения влияющих величин при нормальных условиях
Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью, а также размером допускаемых погрешностей. Точность измерения — характеристика качества измерения, отражающая близость к нулю погрешности его результата. Точность измерения является величиной качественной. Высокая точность измерения соответствует малым погрешностям и наоборот. Иногда точность количественно оценивают обратной величиной модуля относительной погрешности. Например, если погрешность составляет 0,001, то точность равна 1000. Однако количественная оценка точности широкого распространения не получила. Достоверность измерений определяется степенью доверия к результату измерения и характеризуется вероятностью того, что истинное значение измеряемой величины находится в указанных пределах. Данная вероятность называется доверительной. Правильность измерений — это характеристика измерений, отражающая близость к нулю систематических погрешностей результатов измерений. Сходимость результата измерений — характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполняемых повторно одними и теми же методами и средствами измерений и в одних и тех же условиях. Сходимость измерений отражает влияние случайных погрешностей на результат измерения. Воспроизводимость результатов измерений — характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами и средствами измерений, разными операторами, но приведенных к одним и тем же условиям. Количественная близость измеренного и истинного значений измеряемой величины описывается погрешностью результата измерений. Погрешность — это отклонение Х результата измерения Хизм от истинного значения Хнс измеряемой величины, определяемое по формуле Х = Xизм – Xис. В общем виде погрешность измерения может быть описана исходя из основного уравнения измерения (2.1). Неидеальность измерительной процедуры, следствием которой является погрешность результата измерения Q̃ выражается введением в уравнение (2.1) погрешностей всех его элементов:  где Q — результат измерения; [Q]— единица измерения величины; Δq— погрешность нахождения числового значения измеряемой величины; Δ[Q]— погрешность реализации в данном измерении единицы измеряемой величины. Истинное значение и результат измерения принадлежат и к ветви реальностей (см. рис.2.5), и к ветви отражений (моделей). Вследствие принципиальной неадекватности любой модели отражаемой реальности невозможно, оперируя с реальными объектами и СИ в реальных условиях, обеспечить тождественность полученного результата и истинного значения измеряемой величины. Следовательно, принципиально нельзя точно определить погрешность измерения, поскольку в противном случае введением в результат поправки можно найти истинное значение. Учение о погрешностях измерений и средств измерений является одной из центральных тем в теоретической метрологии. Оно подробно рассмотрено в гл. 4-6. Результат измерения и оценка его погрешности находятся субъектом измерения с помощью вычислительных средств (ветвь реальности), работающих по определенному алгоритму обработки измерительной информации (модельная ветвь). Субъект измерения — человек — объединяет в себе обе ветви процесса измерения (реальности и отражения), активно воздействует на него и осуществляет: • постановку измерительной задачи; • сбор и анализ априорной информации об объекте измерения; • анализ адекватности объекту измерения выбранной модели; • обработку результатов измерений. |
