Сергеев - Метрология. В. Г. Фирстов Кандидат физикоматематических наук

• Название: В. Г. Фирстов Кандидат физикоматематических наук
• Анкор: Сергеев - Метрология.doc
• Дата: 28.01.2017
• Размер: 4.38 Mb.
• Имя файла: Сергеев - Метрология.doc
• Тип: Документы; #707
• страница: 6 из 37

2.4. Основные этапы измерений

Измерение — последовательность сложных и разнородных действий, состоящая из ряда этапов [24]. Первым этапом любого измерения является постановка измерительной задачи. Он включает в себя:

• сбор данных об условиях измерения и исследуемой ФВ, т.е. накопление априорной информации об объекте измерения и ее анализ;

• формирование модели объекта и определение измеряемой величины, что является наиболее важным, особенно при решении сложных измерительных задач. Измеряемая величина определяется с помощью принятой модели как ее параметр или характеристика. В простых случаях, т.е. при измерениях невысокой точности, модель объекта в явном виде не выделяется, а пороговое несоответствие пренебрежимо мало;

• постановку измерительной задачи на основе принятой модели объекта измерения;

• выбор конкретных величин, посредством которых будет находиться значение измеряемой величины;

• формулирование уравнения измерения.

Вторым этапом процесса измерения является планирование измерения. В общем случае оно выполняется в следующей последовательности:

• выбор методов измерений непосредственно измеряемых величин и возможных типов СИ;

• априорная оценка погрешности измерения;

• определение требований к метрологическим характеристикам СИ и условиям измерений;

• выбор СИ в соответствии с указанными требованиями;

• выбор параметров измерительной процедуры (числа наблюдений для каждой измеряемой величины, моментов времени и точек выполнения наблюдений);

• подготовка СИ к выполнению экспериментальных операций;

• обеспечение требуемых условий измерений или создание возможности их контроля.

Эти первые два этапа, являющиеся подготовкой к измерениям, имеют принципиальную важность, поскольку определяют конкретное содержание следующих этапов измерения. Подготовка проводится на основе априорной информации. Качество подготовки зависит от того, в какой мере она была использована. Эффективная подготовка является необходимым, но недостаточным условием достижения цели измерения. Ошибки, допущенные при подготовке измерений, с трудом обнаруживаются и корректируются на последующих этапах.

Третий, главный этап измерения — измерительный эксперимент. В узком смысле он является отдельным измерением. В общем случае последовательность действий во время этого этапа следующая:

• взаимодействие средств и объекта измерений;

• преобразование сигнала измерительной информации;

• воспроизведение сигнала заданного размера;

• сравнение сигналов и регистрация результата. Последний этап измерения — обработка экспериментальных

данных. В общем случае она осуществляется в последовательности, которая отражает логику решения измерительной задачи:

• предварительный анализ информации, полученной на предыдущих этапах измерения;

• вычисление и внесение возможных поправок на систематические погрешности;

• формулирование и анализ математической задачи обработки данных;

• построение или уточнение возможных алгоритмов обработки данных, т.е. алгоритмов вычисления результата измерения и показателей его погрешности;

• анализ возможных алгоритмов обработки и выбор одного из них на основании известных свойств алгоритмов, априорных данных и предварительного анализа экспериментальных данных;

• проведение вычислений согласно принятому алгоритму, в итоге которых получают значения измеряемой величины и погрешностей измерений;

• анализ и интерпретация полученных результатов;

• запись результата измерений и показателей погрешности в соответствии с установленной формой представления.

Некоторые пункты данной последовательности могут отсутствовать при реализации конкретной процедуры обработки результатов измерений.

Задача обработки данных подчинена цели измерения и после выбора СИ однозначно вытекает из измерительной задачи и, следовательно, является вторичной. Подробно обработка результатов измерений различных типов рассмотрена в гл. 8.

Перечисленные выше этапы существенно различаются по выполняемым операциям и их трудоемкости. В конкретных случаях соотношение и значимость каждого из этапов заметно варьирует. Для многих технических измерений вся процедура измерения сводится к экспериментальному этапу, поскольку анализ и планирование, включая априорное оценивание погрешности, выбор нужных методов и средств измерений осуществляются предварительно, а обработка данных измерений, как правило, минимизируется.

Выделение этапов измерения имеет непосредственное практическое значение — способствует своевременному осознанному выполнению всех действий и оптимальной реализации измерений. Это в свою очередь позволяет избежать серьезных методических ошибок, связанных с переносом проблем одного этапа на другой.

2.5. Постулаты теории измерений

Как и любая другая наука, метрология строится на основе ряда основополагающих постулатов, описывающих ее исходные аксиомы. Построению и исследованию этих аксиом—постулатов посвящено большое число научных исследований [25]. Однако считать, что исследования в этой области закончены, не представляется возможным. Приведенные в [25] и рассмотренные далее постулаты метрологии будут в дальнейшем безусловно уточняться и дополняться [18].

Следует отметить, что любая попытка сформулировать исходные положения (постулаты) теории измерений встречает принципиальные затруднения. Это связано с тем, что, с одной стороны, постулаты должны представлять собой объективные утверждения, а с другой — предметом метрологии являются измерения, т.е. вид деятельности людей, предпринимаемой ими для достижения субъективных целей. Следовательно, необходимо сформулировать объективные утверждения, которые бы служили фундаментом научной дисциплины, имеющей существенный субъективный элемент. Первым постулатом метрологии является постулат а: в рамках принятой модели объекта исследования существует определенная измеряемая физическая величина и ее истинное значение. Если, например, считать, что деталь представляет собой цилиндр (модель — цилиндр), то она имеет диаметр, который может быть измерен. Если же деталь нельзя считать цилиндрической, например ее сечение представляет собой эллипс, то измерять ее диаметр бессмысленно, поскольку измеренное значение не несет полезной информации о детали. И, следовательно, в рамках новой модели диаметр не существует. Измеряемая величина существует лишь в рамках принятой модели, т. е. имеет смысл только до тех пор, пока модель признается адекватной объекту. Так как при различных целях исследований данному объекту могут быть сопоставлены различные модели, то из постулата  вытекает следствие ₁: для данной физической величины объекта измерения существует множество измеряемых величин (и соответственно их истинных значений).

Итак, из первого постулата метрологии следует, что измеряемому свойству объекта измерений должен соответствовать некоторый параметр его модели. Данная модель в течение времени, необходимого для измерения, должна позволять считать этот ее параметр неизменным. В противном случае измерения цв могут быть проведены. Указанный факт описывается постулатом р: истинное значение измеряемой величины постоянно.

Выделив постоянный параметр модели, можно перейти к измерению соответствующей величины. Для переменной ФВ необходимо выделить или выбрать некоторый постоянный параметр и измерить его. В общем случае такой постоянный параметр вводится с помощью некоторого функционала. Примером таких постоянных параметров переменных во времени сигналов, вводимых посредством функционалов, являются средневыпрямленные или среднеквад-ратические значения. Данный аспект отражается в следствии ₁: для измерения переменной физической величины необходимо определить ее постоянный параметр — измеряемую величину.

При построении математической модели объекта измерения неизбежно приходится идеализировать те или иные его свойства. Модель никогда не может полностью описывать все свойства объекта измерений. Она отражает с определенной степенью приближения некоторые из них, имеющие существенное значение для решения данной измерительной задачи. Модель строится до измерения на основе априорной информации об объекте и с учетом цели измерения. Измеряемая величина определяется как параметр принятой модели, а его значение, которое можно было бы получить в результате абсолютно точного измерения, принимается в качестве истинного значения данной измеряемой величины. Эта неизбежная идеализация, принятая при построении модели объекта измерения, обуславливает неизбежное несоответствие между параметром модели и реальным свойством объекта, которое называется пороговым. Принципиальный характер понятия "пороговое несоответствие" устанавливается постулатом : существует несоответствие измеряемой величины исследуемому свойству объекта (пороговое несоответствие измеряемой величины). Пороговое несоответствие принципиально ограничивает достижимую точность измерений при принятом определении измеряемой ФВ.

Изменения и уточнения цели измерения, в том числе и такие, которые требуют повышения точности измерений, приводят к необходимости изменять или уточнять модель объекта измерений и переопределять понятие измеряемой величины. Основной причиной переопределения является то, что пороговое несоответствие ранее принятого определения не позволяет повысить точность измерения до уровня требуемой. Вновь введенный измеряемый параметр модели также может быть измерен лишь с погрешностью, которая в лучшем случае равна погрешности, обусловленной пороговым несоответствием. Поскольку принципиально невозможно построить абсолютно адекватную модель объекта измерения, то нельзя устранить пороговое несоответствие между измеряемой ФВ и описывающим ее параметром модели объекта измерений. Отсюда вытекает важное следствие ₁: истинное значение измеряемой величины отыскать невозможно.

Модель можно построить только при наличии априорной информации об объекте измерения. При этом чем больше информации, тем более адекватной будет модель и соответственно точнее и правильнее будет выбран ее параметр, описывающий измеряемую ФВ. Следовательно, увеличение априорной информации уменьшает пороговое несоответствие. Данная ситуация отражается в следствии ₂: достижимая точность измерения определяется априорной информацией об объекте измерения.

Из этого следствия вытекает, что при отсутствии априорной информации измерение принципиально невозможно. В то же время максимально возможная априорная информация заключается в известной оценке измеряемой величины, точность которой равна требуемой. В этом случае необходимости в измерении нет.

В заключение подчеркнем, что приведенные постулаты и их следствия являются лишь одной из попыток построить теоретический фундамент метрологии и их не следует считать истиной в конечной инстанции.

2.6. Классификация измерений

Обоснованная классификация любых объектов представляет собой их условное группирование по заданным признакам, осуществляемое с определенной целью. При различных целях одни и те же объекты могут быть классифицированы по-разному. Классификация не является самоцелью, она диктуется потребностями теории и практики. Целесообразность классификации измерений, т.е. подразделение этого понятие на группы, обуславливается удобством при разработке методик выполнения измерений и обработки результатов. Измерения могут быть классифицированы по ряду признаков.

Наибольшее распространение получила классификация по общим приемам получения результатов измерений. Согласно этому признаку, измерения делятся на прямые, косвенные, совместные и совокупные. Целью такого деления является удобство выделения методических погрешностей измерений, возникающих при определении результатов измерений.

Прямыми называются измерения, при которых искомое значение величины находят непосредственно по показаниям СИ. Например, масса, измеряемая при помощи весов, температура — термометром, напряжение — вольтметром.

Косвенные измерения — это измерения, при которых значение измеряемой величины находят на основании известкой зависимости между ней и величинами, подвергаемыми прямым измерениям, которые проводились в одинаковых условиях. Такие измерения имеют весьма важное значение для метрологической практики. На их основе, например, устанавливают значения, приписываемые эталонам единиц производных ФВ, исходя из значений единиц основных величин, воспроизводимых первичными эталонами. Широко применяются и менее точные косвенные измерения.

В общем случае зависимость, связывающую измеряемую величину Y и величины X₁, Х₂, ..., Х_п, подвергаемые прямым измерениям, можно представить в виде

(2.3)

Например, измерение плотности р = m/V по результатам прямых измерений массы m и объема V; измерение активного сопротивления R=U/I по результатам прямых измерений напряжения U и тока I.

По виду функциональной зависимости F различают косвенные измерения:

• с линейной зависимостью

—постоянный коэффициент 1-го аргумента;

• с нелинейной зависимостью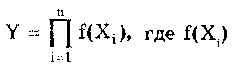


— некоторые функции;
• измерения с зависимостями смешанного типа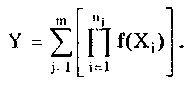



Вид связи между Y и X_i определяет методику расчета погрешностей косвенных измерений.

В современных микропроцессорных измерительных приборах очень часто вычисления искомой измеряемой величины производятся "внутри" прибора. В этом случае результат измерения определяется способом, характерным для прямых измерений, и нет необходимости и возможности отдельного учета методической погрешности расчета. Она входит в погрешность измерительного прибора. Измерения, проводимые такого рода средствами измерений, относятся к прямым. К косвенным относятся только такие измерения, при которых расчет осуществляется вручную или автоматически, но после получения результатов прямых измерений. При этом может быть учтена отдельно погрешность расчета. Характерный пример такого случая — измерительные системы, для которых нормированы метрологические характеристики их компонентов по отдельности. Суммарная погрешность измерений рассчитывается по нормированным метрологическим характеристикам всех компонентов системы.

Совокупными называются проводимые одновременно измерения нескольких одноименных величин, при которых их искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Совместными называются проводимые одновременно измерения двух или нескольких неодноименных величин для установления зависимости между ними. Как видно из приведенных определений, эти два вида измерений весьма близки друг к другу. В обоих случаях искомые значения находятся в результате решения системы уравнений, коэффициенты в которых получены путем прямых измерений. Отличие состоит в том, что при совместных измерениях одновременно определяются несколько одноименных величин, а при совокупных — разноименных.

Косвенные, совместные и совокупные измерения объединяются одним принципиально важным общим свойством: их результаты определяются расчетом по известным функциональным зависимостям между измеряемыми величинами и величинами, подвергаемыми прямым измерениям. Различие между этими видами измерений заключается только в виде функциональной зависимости, используемой при расчетах. При косвенных измерениях она выражается одним уравнением в явном виде (2.3), при совместных и совокупных — системой неявных уравнений. Поэтому уже неоднократно высказывались мнения [7] о сокращении "приведенной выше классификации. Все измерения делят на прямые и косвенные, которые в свою очередь подразделяются на несколько групп, различающихся между собой видом уравнений, представляющих функциональные зависимости между измеряемыми величинами и величинами, подвергаемыми прямым измерениям.

По характеристике точности измерения делятся на равноточные и неравноточные.

Равноточными называются измерения какой-либо ФВ, выполненные одинаковыми по точности СИ и в одних и тех же условиях. Соответственно неравноточными называются измерения ФВ, выполненные различными по точности СИ и (или) в разных условиях. Методика обработки результатов равноточных и неравноточных измерений различна.

В зависимости от числа измерений, проводимых во время эксперимента, различают одно- и многократные измерения. Однократными называются измерения, выполненные один раз, к многократными относятся измерения одного и того же размера ФВ, следующие друг за другом. Известно, что при числе отдельных измерений более четырех их результаты могут быть обработаны в соответствии с требованиями математической статистики. Это означает, что при четырех и более измерениях, входящих в ряд, измерения можно считать многократными. Их проводят с целью уменьшения случайной составляющей погрешности.

По отношению к изменению измеряемой величины измерения делятся на статические и динамические. Целью данной классификации является возможность принятия решения о том, нужно ли при конкретных измерениях учитывать скорость изменения измеряемой величины или нет. Погрешности, вызываемые влиянием скоростей изменения измеряемой величины, называются динамическими.

К статическим относятся измерения ФВ, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Динамические измерения — это измерения изменяющейся по размеру ФВ. Признаком, по которому измерение относят к статическому или динамическому, является динамическая погрешность при данной скорости или частоте изменения измеряемой величины и заданных динамических свойствах СИ. Предположим, что она пренебрежимо мала (для решаемой измерительной задачи). В этом случае измерение можно считать статическим. При невыполнении указанных требований оно является динамическим.

В зависимости от метрологического назначения измерения делятся на технические и метрологические. Технические измерения проводятся рабочими СИ. Метрологические измерения выполняются при помощи эталонов с целью воспроизведения единиц ФВ для передачи их размера рабочим СИ.

При метрологических измерениях в обязательном порядке учитываются погрешности, а при технических — принимается наперед заданная погрешность, достаточная для решения данной практической задачи. Поэтому при технических измерениях нет необходимости определять и анализировать погрешности получаемых результатов. Технические измерения являются наиболее массовым видом.

В зависимости от выражения результатов измерений последние подразделяются на абсолютные и относительные. Абсолютное измерение основано на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Понятие "абсолютное измерение" применяется как противоположное понятию "относительное измерение" и рассматривается как определение величины в ее единицах.

Относительное измерение — это измерение отношения определяемой величины к одноименной. Например: измерение активности радионуклида в источнике по отношению к активности радионуклида в однотипном источнике, аттестованном в качестве образцовой меры активности. Относительные измерения при прочих равных условиях могут быть выполнены более точно, чем абсолютные, поскольку в суммарную погрешность не входит погрешность меры величины.

2.7. Понятие об испытании и контроле

Испытанием называется экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как результата воздействия на него при его функционировании, а также моделировании объекта и (или) воздействий (ГОСТ 16504-91). Экспериментальное определение характеристик свойств объекта при испытаниях может проводиться путем использования измерений, оценивания и контроля.

Объектом испытаний является продукция или процессы ее производства и функционирования. В зависимости от вида продукции и программы испытаний объектом может быть как единичное изделие, так и их партия. Объектом испытания может также быть макет или модель изделия.

Важнейшими признаками любых испытаний являются:

• принятие на основе их результатов определенных решении по объекту испытаний, например о его годности или забраковке, о возможности предъявления на следующие испытания и т.д.;

• задание требуемых реальных или моделируемых условий испытаний. Под условиями испытаний понимается совокупность воздействующих факторов и (или) режимов функционирования объекта при испытаниях. В нормативно-технических документах на испытания конкретных объектов должны быть определены нормальные условия испытаний.

Существует большое число разновидностей испытаний. Они классифицируются по различным признакам. По назначению испытания делятся на исследовательские, контрольные, сравнительные и определительные. По уровню проведения различают следующие категории испытаний: государственные, межведомственные и ведомственные. По виду этапов разработки испытуемой продукции различают предварительные и приемочные испытания. В зависимости от вида испытаний готовой продукции их подразделяют на квалификационные, приемосдаточные периодические и типовые. Определения этих видов испытаний можно найти в ГОСТ 16504-81 "Система государственных испытаний продукции. Испытания и контроль качества продукции. Основные термины и определения".

Целью испытаний следует считать нахождение истинного значения параметра (характеристики), определенного не при тех реальных условиях, в которых он фактически может находится в ходе испытаний, а в заданных номинальных условиях испытания. Реальные условия испытаний практически всегда отличаются от номинальных, поскольку установить параметры условий испытаний абсолютно точно невозможно. Следовательно, результат испытания всегда имеет погрешность, возникающую не только из-за погрешности определения искомой характеристики, но и из-за неточного установления номинальных условий испытания.

Результатом испытаний называется оценка характеристик свойств объекта, установления соответствия объекта заданным требованиям, данные анализа качества функционирования объекта в процессе испытаний. Результат испытаний характеризуется точностью — свойством испытаний, описывающим близость их результатов к действительным значениям характеристик объекта в определенных условиях испытаний.

Между измерением и испытанием существует большое сходство: во-первых, результаты обеих операций выражаются в виде чисел; во-вторых, погрешности и в том, и другом случае могут быть выражены как разности между результатами измерений (испытаний) и истинными значениями измеряемой величины (или определяемой характеристики при номинальных условиях эксплуатации). Однако с точки зрения метрологии между этими операциями имеется значительная разница: погрешность измерения является только одной из составляющих погрешности испытания. Поэтому можно сказать, что испытание — это более общая операция, чем измерение. Измерение можно считать частным случаем испытания, при котором условия испытаний не представляют интереса.
Пример 2.4. Рассмотрим испытания магнитных свойств магнитомягких материалов, проводимых в соответствии с ГОСТ 12119-80. Их целью является определение характеристик и параметров магнитных материалов, таких как основная кривая намагничивания, кривая удельных магнитных потерь, коэрцитивная сила, остаточная индукция, индукция насыщения и др.

Для того чтобы измерить эти характеристики и параметры, образец необходимо перемагнитить. Значения магнитных величин существенно зависят от режима перемагничивания испытуемого образца, поэтому с целью получения возможности сравнения результатов измерений различных лабораторий стандарт предписывает:

• использовать при испытаниях образцы магнитных материалов стандартизованной формы (кольцевые и полоски для аппарата Эпштейна);

• применять унифицированные первичные преобразователи магнитных свойств (см. пример 11.4 в разд. 11.5);

• проводить измерения при регламентированном законе изменения магнитной индукции в процессе перемагничивания образца. Основное распространение получил синусоидальный закон, который необходимо обеспечивать с погрешностью (по коэффициенту гармоник) не более 2%. Отличие реального закона изменения магнитной индукции от синусоидального в пределах более допустимых значений приводит к погрешностям определения магнитных параметров.
Контроль — это процесс определения соответствия значения параметра изделия установленным требованиям или нормам. Сущность всякого контроля состоит в проведении двух основных этапов. На первом из них получают информацию о фактическом состоянии некоторого объекта, о признаках и показателях его свойств. Эта информация называется первичной. На втором — первичная информация сопоставляется с заранее установленными требованиями, нормами, критериями. При этом выявляется соответствие или несоответствие фактических данных требуемым. Информация о их расхождении называется вторичной. Она используется для выработки соответствующих решений по поводу объекта контроля. В ряде случаев граница между этапами контроля неразличима. При этом первый этап может быть выражен нечетко или практически не наблюдаться. Характерным примером такого рода является контроль размера детали калибром, сводящийся к операции сопоставления фактического и предельно допустимого значений параметра.

Контроль состоит из ряда элементарных действий: измерительного преобразования контролируемой величины; операции воспроизведения уставок контроля; операции сравнения; определения результата контроля.

Измерения и контроль тесно связаны друг с другом, близки по своей информационной сущности и содержат ряд общих операций (например, сравнение, измерительное преобразование). В то же время их процедуры во многом различаются:

• результатом измерения является количественная характеристика, а контроля — качественная;

• измерение осуществляется в широком диапазоне значений измеряемой величины, а контроль — обычно в пределах небольшого числа возможных состояний;

• контрольные приборы, в отличие от измерительных, применяются для проверки состояния изделий, параметры которых заданы и изменяются в узких пределах;

• основной характеристикой качества процедуры измерения является точность, а процедуры контроля — достоверность.

Контроль может быть классифицирован по ряду признаков.

В зависимости от числа контролируемых параметров он подразделяется на однопараметровый, при котором состояние объекта определяется по размеру одного параметра, и многопараметровый, при котором состояние объекта определяется размерами многих параметров.

По форме сравниваемых сигналов контроль подразделяется на аналоговый, при котором сравнению подвергаются аналоговые сигналы, и цифровой, при котором сравниваются цифровые сигналы.

В зависимости от вида воздействия на объект контроль подразделяется на пассивный, при котором воздействие на объект не производится, и активный, при котором воздействие на объект осуществляется посредством специального генератора тестовых сигналов.

В практике большое распространение получил так называемый допусковый контроль [26], суть которого состоит в определении путем измерения или испытания значения контролируемого параметра объекта и сравнение полученного результата с заданными граничными допустимыми значениями. Частным случаем допускового контроля является поверка средств измерений, в процессе которой исследуется попадание погрешностей средства измерений в допускаемые пределы.

По расположению зоны контролируемого состояния различают допусковый контроль состояний:

• ниже допускаемого значения X < Х_н;

• выше допускаемого значения X > Х_в;

• между верхним и нижним допускаемыми значениями Х_н< X < Х_в. Результатом контроля является не число, а одно из взаимоисключающих утверждений:

• "контролируемая характеристика (параметр) находится в пределах допускаемых значений", результат контроля — "годен";

• "контролируемая характеристика (параметр) находится за пределами допускаемых значений", результат контроля —"не годен" или "брак".

Для определенности примем, что решение "годен" должно приниматься, если выполняется условие Х_н XХ_в, где X, Х_в Х_н— истинное значение и допускаемые верхнее и нижнее значения контролируемого параметра. На самом же деле с допускаемыми значениями Х_в и Х_н сравнивается не истинное значение X (поскольку оно неизвестно), а его оценка Х₀, полученная в результате измерений. Значение Х₀ отличается от X на величину погрешности измерения: Х = Х₀ + . Решение "годен" при проведении контроля принимается в случае выполнения неравенства Х_Н  Х₀  Х_В. Отсюда следует, что при допусковом контроле возможны четыре исхода.

1.Принято решение "годен", когда значение контролируемого параметра находится в допускаемых пределах, т.е. имели место события Х_н XХ_в и

Х_Н  Х₀  Х_В. Если известны плотности вероятностей законов распределения f(X) контролируемого параметра X и погрешности его измерения f(), то при взаимной независимости этих законов и заданных допустимых верхнем и нижнем значениях параметра вероятность события "годен"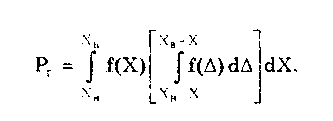


2. Принято решение "брак", когда значение контролируемого параметра находится вне пределов допускаемых значений, т.е. имели место события X < Х_рили X > Х_в и Х₀ < Хнили Х₀ > X_в. При оговоренных допущениях вероятность события "негоден" или "брак"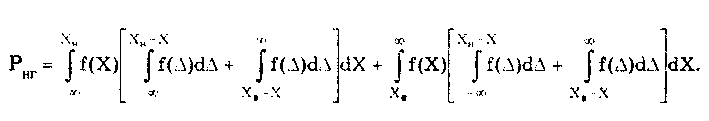


3. Принято решение "брак", когда истинное значение контролируемого параметра лежит в пределах допускаемых значений, т.е. Х₀ < Х_Н или Х₀ > Х_в и Х_н £X£Х_в и забракован исправный объект. В этом случае принято говорить, что имеет место ошибка I рода. Ее вероятность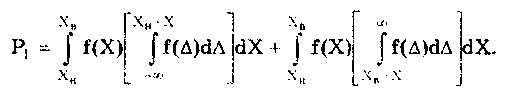


4. Принято решение "годен", когда истинное значение контролируемого параметра лежит вне пределах допускаемых значений, т.е. имели место события X < Х_нили Х > Х_в и Х_Н £ Х₀ £ Х_В и неисправный объект признан годным. В этом случае говорят, что произошла ошибка II рода, вероятность которой


Очевидно, что ошибки I и II родов имеют разное значение для изготовителей и потребителей (заказчиков) контролируемой продукции [26]. Ошибки I рода ведут к прямым потерям изготовителя, так как ошибочное признание негодным в действительности годного изделия приводит к дополнительным затратам на исследование, доработку и регулировку изделия. Ошибки II рода непосредственно сказываются на потребителе, который получает некачественное изделие. При нормальной организации отношений между потребителем и производителем брак, обнаруженный первым из них, приводит к рекламациям и ущербу для изготовителя.

Рассмотренные вероятности Р_г, Р_нг , Р₁, и Р₂, при массовом контроле партии изделий характеризуют средние доли годных, негодных, неправильно забракованных и неправильно пропущенных изделий среди всей контролируемой их совокупности. Очевидно, что P_г + P_нг + P₁ + P₂ = 1.

Достоверность результатов допускового контроля описывается различными показателями [9, 26, 56], среди которых наибольшее распространение получили вероятности ошибок I (P₁) и II (Р₂) родов и риски изготовителя и заказчика (потребителя):



Одна из важнейших задач планирования контроля — выбор оптимальной точности измерения контролируемых параметров. При завышении допускаемых погрешностей измерения уменьшается стоимость средств измерений, но увеличиваются вероятности ошибок при контроле, что в конечном итоге приводит к потерям. При занижении допускаемых погрешностей стоимость средств измерений возрастает, вероятность ошибок контроля уменьшается, увеличивает себестоимости выпускаемой продукции. Очевидно, что существует некоторая оптимальная точность, соответствующая минимуму суммы потерь от брака и стоимости контроля.

Приведенные формулы позволяют осуществить целенаправленный поиск таких значений погрешности измерения, которые бы при заданных верхнем и нижнем значениях Контролируемого параметра обеспечили бы допускаемые значения вероятностей ошибок I и II родов (Р_!д и Р_2д) или соответствующих рисков. Этот поиск производится путем численного или графического интегрирования. Следовательно, для рационального выбора точностных характеристик средств измерений, используемых при проведении контроля, в каждом конкретном случае должны быть заданы допускаемые значения Р_1д и Р_2д.
Контрольные вопросы
1. Дайте определение физической величины. Приведите примеры величин, принадлежащих к различным группам физических процессов.

2. Что такое экстенсивные и интенсивные физические величины? В чем их сходство и различие? Приведите примеры ФВ каждого вида.

3. Проанализируйте определения счета, оценивания и измерения. Выделите их общие и отличительные признаки.

4. Что такое шкала физической величины? Приведите примеры различных шкал ФВ.

5. Назовите основные операции процедуры измерения. Расскажите, как они реализуются при измерении размера детали штангенциркулем.

6. Приведите примеры измерительных преобразователей, многозначных мер и устройств сравнения, используемых в известных вам средствах измерений.

7. Какие элементы процесса измерений принадлежат к ветви реального, а какие — к ветви отражения реальности? Как они соотносятся друг с другом?

8. По каким признакам классифицируются методы измерений? Какие методы измерений вам известны?

9. Что такое средство измерений? Приведите примеры средств измерений различных ФВ.

10. Что такое условия измерений? Какие они бывают?

11. Что такое результат измерения и чем он характеризуется?

12. Сформулируйте основные этапы измерения применительно к процессу измерения микрометром диаметра детали.

13. Перечислите признаки, по которым могут быть классифицированы измерения. Расскажите о классификации измерений по каждому из названных признаков.

14. Дайте определения прямых, косвенных, совместных и совокупных измерений. Приведите примеры измерений каждого вида.

15. Что такое испытание и чем оно отличается от измерения?

16. Что такое контроль и чем он отличается от измерения? Какие виды контроля существуют?

17. Что такое вероятность ошибок I и II родов? Что они характеризуют?