В геодезии применяются следующие виды масштабов. В геодезии применяются следующие виды масштабов численный ( применяется всегда)
 Скачать 271.93 Kb. Скачать 271.93 Kb.
|
|
В геодезии применяются следующие виды масштабов: 1. численный ( применяется всегда) 2. именованный (словесный) масштаб 3.линейный ( применяются для удобства и повышения скорости обработки материалов съемок). 4. поперечный 5. масштаб шагов ( применяется при глазомерных съемках). 6. масштаб времени МАСШТАБ – это степень уменьшения, выраженная отношением длины отрезка линии на плане (профиле) к соответствующей ей проекции на местности. Численный масштаб – это дробь, у которой числитель, равный единице, показывает длину отрезка на плане (профиле), а знаменатель – соответствующую ей длину проекции отрезка на местности. - 1:1000 – в 1 см -10м; в 1 мм – 1 м - 1: 2000 - в 1 см – 20 м; в 1 мм - 2 м. В зависимости от величины знаменателя различают мелкие и крупные масштабы, чем больше знаменатель, тем мельче масштаб и наоборот. Именованный (словесный) масштаб - вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке. Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре. - в 1 сантиметре 5 километров (в 1 см 5 км). Линейный масштаб – это график, построенный для работы с данной картой по ее численному масштабу. График имеет вид прямой, разделенной на равные отрезки ( основания). Слева от нуля графика оставляют один отрезок и делят его 10 частей. Вправо от нуля в конце каждого отрезка надписывают числа метров местности соответствующие расстояниям концов от нуля.  Рис.4 Линейный масштаб Длина отрезка, который откладывают по линии при построении масштаба, называется его основанием. Поперечный масштаб строится для точности работы с планом или картой, при чем график является универсальным, т.е. имея этот график можно работать с любой картой или планом. Наименьшее деление поперечного масштаба t = 0,01 основания. Невооруженным глазом при нормальном зрении можно различать точки, удаленные друг от друга на 0,01 см или 0,1мм. Расстояние на местности, которое соответствует 0,01 см на плане, называется точностью масштаба. 2. Теория и построение поперечного масштаба, его точность. 2.1 Построение поперечного масштаба. При пользовании простым линейным масштабом приходится мелкие доли в крайнем левом основании отсчитывать на глаз. Чтобы эти отсчеты были более точными и надежными, употребляют особых вид линейного масштаба, который называется поперечным. Для получения поперечного масштаба сначала выполняют на горизонтальной линии ММ построение простого линейного масштаба. Затем из концов отложенных оснований восстанавливают вверх от линии ММ перпендикуляры МN, ob, 2—2 и т. д. Левые нижние и верхние основания Мо и Nb делят на 10 равных частей и точки деления соединяют, как показано на рисунке, косыми линиями, называемыми-трансверсалями. 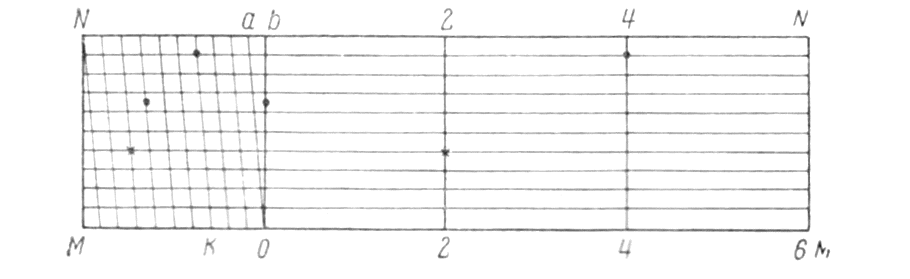 Рис. 5 Поперечный масштаб Полученный чертеж и называется поперечным масштабом. Из построения его следует, что расстояния между соседними трансверсалями по параллелям равны 0.1 ℓ. Расстояния же от перпендикуляра ob до первой трансверсали оа при переходе от параллели к параллели изменяются. Изобразим треугольник abo в увеличенном виде (рис. 6) и обратим в нем внимание на расстояние a1b1=t , которое является наименьшим. Из подобия прямоугольных треугольников a1b1 с1иabo имеем: t : ab = ob1: ob; t = ab*ob1/ob . Здесь по построению ab =0,1 ℓ и оb1: оb=0,1; следовательно. t =0,01ℓ, 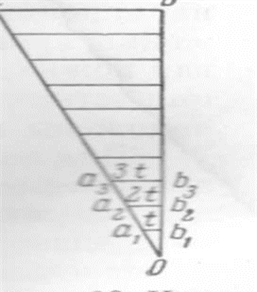 Рис.6 т. е. наименьшее деление поперечного масштаба составляет 0,01 основания масштаба. Из подобия треугольников a2b2о и abо, затем a3b3о и abо и т.д. аналогично получим: a2b2=0.02l=2t a3b3=0.03l=3t и т. д., т. е. при переходе вверх с параллели на соседнюю параллель расстояния от перпендикуляра оb до первой трансверсали увеличиваются на величину наименьшего деления. Очевидно, что точки пересечения любой трансверсали с параллелями при переходе с параллели на параллель вверх сдвигаются влево от перпендикулярного положения на ту же величину. Описанный поперечный масштаб называется сотенным или нормальным. Теоретически при построении поперечного масштаба можно как первое левое основание, так и расстояние вверх по перпендикулярам делить не обязательно на 10, а на какое угодно другое число равных частей. Разница будет только в том, что наименьшее деление его будет составлять другую долю от основания. Обозначим в общем виде число частей основания буквой т и число частей, отложенных по перпендикуляру вверх, буквой п. В таком случае наименьшее деление выразится формулой: t=l/mn 2.2 Пользование поперечным масштабом. Для практического использования на заводах изготовляют специальные металлические масштабные линейки, на которых с помощью особых делительных машин гравируют нормальные поперечные масштабы с основанием 2 см. Подписи на них дают в сантиметрах. На рисунке 5 изображена левая часть такого масштаба. В конце правой части гравируют также пятидесятенный масштаб, у которого основание разделено на 5 равных частей, так что по нему можно непосредственно учитывать 0,02 основания, т. е. 0,04 см. Пользование поперечным масштабом непосредственно вытекает из его теории. Пусть, например, требуется взять в раствор измерителя 4,78 см. На нижней горизонтальной линии ММ непосредственно можно взять расстояние 4.60 см (расстояние 4 — к). Для заданного отсчета это расстояние нужно увеличить на 0,18 см, для чего левая ножка измерителя должна быть передвинута по трансверсали к вверх на девятую параллель (так как 0,18 =0,02*9). На этой параллели ножки измерителя устанавливают в точки, отмеченные на рисунке кружками. Крестиками на 4-й параллели отмечено расстояние 3,48 см. Практически ножки измерителя можно устанавливать на глаз посредине между параллелями и таким образом учитывать сотые доли сантиметра. Например, если ножки поставить посредине между 6-й и 7-й параллелями, как отмечено на рисунке точками, то взятое расстояние будет 1.33 см. Для измерения линии, начерченной на бумаге, ее берут в раствор измерителя и прикладывают его к масштабу так, чтобы левая ножка находилась в пределах крайнего левого основания, а правая все время точно совмещалась с каким-либо перпендикуляром правее нуля. Передвигая в этом положении измеритель вверх, добиваются, чтобы левая ножка точно совместилась с пересечением ближайшей левой от нее трансверсали с некоторой параллелью, на которой должна находиться и правая ножка. В этом положении производят отсчеты: по перпендикуляру, с которым совмещена правая ножка, целые сантиметры, по нижним делениям крайнего левого основания четные десятые доли сантиметра и по номеру параллели, на которой расположены ножки измерителя, четные сотые доли сантиметра. Для перехода от длин линий на местности к длинам их на плане и обратно поперечные масштабы подписываются, как было указано для простых линейных масштабов. Если при переходах пользоваться масштабной линейкой, то предварительно следует установить значения его делений в соответствии с численным масштабом. Например, для масштаба 1 : 25 000 основание составит 500 м, деления крайнего левого основания будут по 50м и наименьшее деление масштаба — 5 м. 3. Способы определения длин линий, измеренных на плане Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба. Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 7); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825). 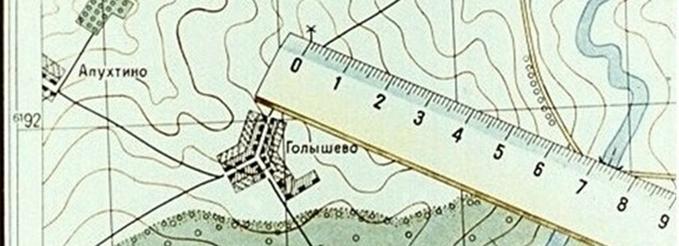 Рис. 7. Определение по карте расстояние между точками местности с помощью линейки. Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 8). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м. 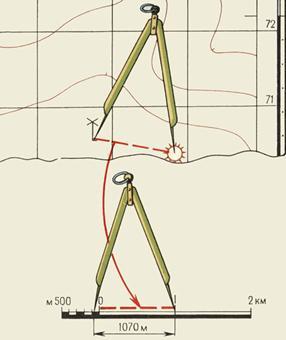 Рис. 8. Измерение на карте расстояний циркулем-измерителем по линейному масштабу 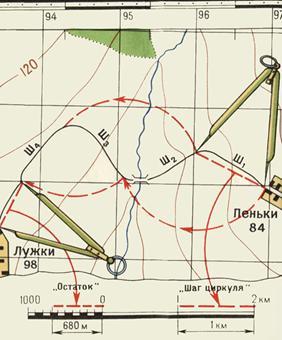 Рис. 9. Измерение на карте расстояний циркулем-измерителем по извилистым линиям Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя. В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 7). Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров. Таким же способом измеряют расстояния по извилистым линиям (рис. 9). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии. 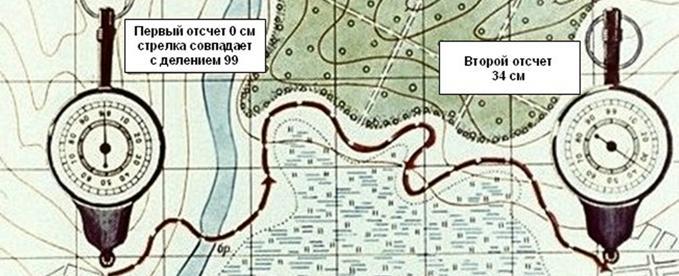 Рис. 10. Измерения расстояния курвиметром Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 10), который особенно удобен для измерения извилистых и длинных линий. В приборе имеется колесико, которое соединено системой передач со стрелкой. При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м) Точность измерения расстояний по карте. Поправки на расстояние за наклон и извилистость линий. Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов. Наиболее точно определить расстояние по карте можно по прямой линии. При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0,7-1 мм в масштабе карты, что составляет для карты масштаба 1:25000 - 17,5-25 м, масштаба 1:50000 – 35-50 м, масштаба 1:100000 – 70-100 м. В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость. Например, При крутизне ската 20° (рис. 11) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше. Подсчитано, что при угле наклона (крутизне ската) 20° полученный результат измерения расстояния по карте следует увеличивать на 6% (на 100 м прибавлять 6 м), при угле наклона 30° - на 15%, а при угле 40° - на 23%. 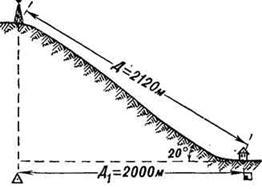 Рис. 11. Проекция длины ската на плоскость (карту) При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний. Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах. Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице. Простейшие способы измерения площадей по карте. Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки, имеющейся на карте. Каждому квадрату сетки карт масштабов 1:10000 - 1:50000 на местности соответствует 1 км2 , квадрату сетки карт масштаба 1:100000 - 4 км2, квадрату сетки карт масштаба 1:200000 - 16 км2. Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений). Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта. По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников {в гектарах ) указаны на линейке для каждого масштаба карты. Масштабы топографических карт
Ниже приведены численые маштабы карт и соответствующие им именованые масштабы: Масштаб 1: 100 000 1 мм на карте - 100 м (0,1 км) на местности 1 см на карте - 1000 м (1 км) на местности 10 см на карте - 10000 м (10 км) на местности Масштаб 1:10000 1 мм на карте – 10 м (0,01 км) на местности 1 см на карте - 100 м (0,1 км) на местности 10 см на карте - 1000м (1 км) на местности Масштаб 1:5000 1 мм на карте – 5 м (0,005 км) на местности 1 см на карте - 50 м (0,05 км) на местности 10 см на карте – 500 м (0,5 км) на местности Масштаб 1:2000 1 мм на карте – 2 м (0,002 км) на местности 1 см на карте – 20 м (0,02 км) на местности 10 см на карте – 200 м (0,2 км) на местности Масштаб 1:1000 1 мм на карте – 100 см (1 м) на местности 1 см на карте – 1000см (10 м) на местности 10 см на карте – 100 м на местности Масштаб 1:500 1 мм на карте – 50 см (0,5 метра) на местности 1 см на карте – 5 м на местности 10 см на карте – 50 м на местности Масштаб 1:200 1 мм на карте –0,2 м (20 см) на местности 1 см на карте – 2 м (200 см) на местности 10 см на карте – 20 м (0,2 км) на местности Масштаб 1:100 1 мм на карте – 0,1 м (10 см) на местности 1 см на карте – 1 м (100 см) на местности 10 см на карте – 10м (0,01 км) на местности Пример 1. Переведите численный масштаб карты в именованный: а) 1 : 200 000 б) 1 : 10 000 000 в) 1 : 25 000 Решение: Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе. Например, в масштабе 1 : 500 000 в знаменателе после цифры 5 находится пять нулей. Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте. Пример для масштаба 1 : 500 000 В знаменателе после цифры — пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности. Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте. Если, например, в знаменателе масштаба 1 : 10 000 закроем два нуля, получим: в 1 см — 100 м. Ответы: а) в 1 см — 2 км; б) в 1 см — 100 км; в) в 1 см — 250 м. Используйте линейку, накладывайте на карты для облегчения измерения расстояний. Пример 2. Переведите именованный масштаб в численный: а) в 1 см — 500 м б) в 1 см — 10 км в) в 1 см — 250 км Решение: Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры. Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей. Например, для именованного масштаба в 1 см — 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1 : 10 000. Для масштаба в 1 см — 5 км приписываем к пятерке пять нулей и получаем: 1 : 500 000. Ответы: а) 1 : 50 000; б) 1 : 1 000 000; в) 1 : 25 000 000. Карты в зависимости от масштабов условно подразделяют на следующие типы: ▪ топографические планы — 1:400 - 1:5 000; ▪ крупномасштабные топографические карты — 1:10 000 - 1:100 000; ▪ среднемасштабные топографические карты — от 1:200 000 - 1:1 000 000; ▪ мелкомасштабные топографические карты — менее 1:1 000 000. |
