В. И. Швецов Базы данных
 Скачать 8.45 Mb. Скачать 8.45 Mb.
|
9.4.4. В-деревоСтруктура В-дерева (сбалансированное дерево) является следствием дальнейшего расширения концепции использования индексов (строится индекс над индексом) и представляет собой многоуровневые индексы. В--дерево строится следующим образом. Последовательность записей, соответствующая записям исходной таблицы, упорядочивается по значениям первичного ключа. Логические записи объединяются в блоки (по k записей в блоках). Значением ключа блока является минимальное значение ключа у записей, входящих в блок. Последовательность блоков представляет собой последний уровень В-дерева. Строится индекс предыдущего уровня. Записи этого уровня содержат значение ключа блока следующего уровня и указатель-адрес связи соответствующего блока; записи этого уровня также объединяются в блоки (по k записей). Затем аналогично строится индекс более высокого уровня и т.д., пока количество записей индекса на определенном уровне будет не более k. Рассмотрим процедуру работы с B-деервом на примере. Пусть имеется файл экземпляров логических записей, ключи которых принимают значения 2, 7, 8, 12, 15, 27, 28, 40, 43, 50. Для определенности возьмем k=2 (в блок объединяем по 2 экземпляра записей). Построенное для этого примера В-дерево изображено на рис. 9.7 (для упрощения рисунка на уровне 4 представлены только ключи логических записей и не представлены значения других полей этих записей). 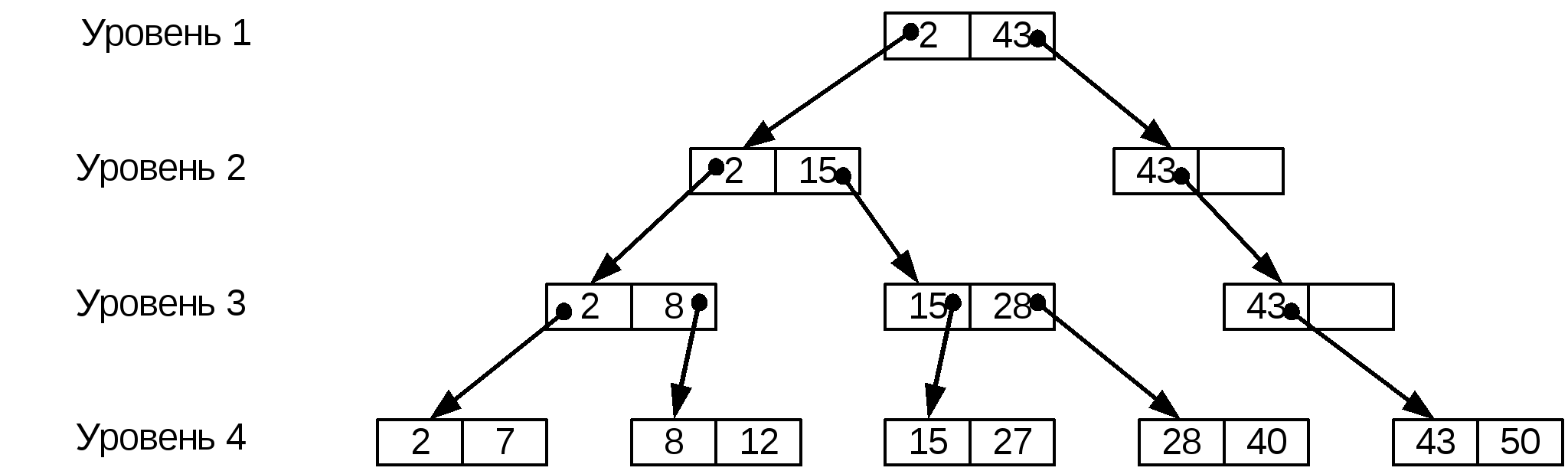 Рис. 9.7. В-дерево В блоках указано значение ключа соответствующего блока. Значение k принято равным 2. По построению В-дерева все исходные записи находятся на одном расстоянии от верхнего индекса (дерево является сбалансированным). Рассмотрим реализацию основных операций. Поиск и чтение записи с заданным значением ключа Читается верхний индекс. Сравниваем заданное значение ключа со значением ключа записей индекса. Если заданное значение ключа больше, чем значение ключа очередной записи индекса (если такая запись имеется), или равно ему, то по адресу связи, указанному в текущей записи, читается блок записей индекса следующего уровня. Далее процесс повторяется. Считаем, что все блоки расположены в ВП. Тогда число обращений к ВП при поиске информации будет равно числу уровней дерева. Число уровней дерева равно минимальному значению l, при котором выполняется условие kl ≥ N (N – число логических записей). Модификация (корректировка) записи После поиска и чтения записи изменяются корректируемые поля. Если корректируется не ключ записи, то измененная запись заносится на свое место. Если изменено значение ключа, то старая запись удаляется (в соответствующем блоке появляется «пустая» запись), а измененная запись заносится так же, как вновь добавляемая. Удаление записи После поиска найденная запись удаляется (в соответствующий блок на место этой записи заносится «пустая» запись). Добавление записи Прежде всего определяется, где должна быть расположена добавляемая запись с заданным значением ключа. Процедура поиска блока, где должна быть расположена эта запись, аналогична вышеописанной процедуре поиска записей с заданным значением ключа. Если в найденном блоке низшего уровня есть «пустая» запись, добавляемая запись заносится в этот блок (с необходимым переупорядочением записей внутри блока). Если в соответствующем блоке низшего уровня нет пустого места, блок делится на два блока. В первый из них заносится [k/2] записей, во второй заносятся остальные. Значением ключа каждого из указанных блоков будет являться, как и описано ранее, минимальное значение ключей у записей, входящих в блок. Добавляемая запись заносится в тот блок, значение ключа которого меньше значения ключа добавляемой записи. Появление нового блока с новым значением ключа обусловливает необходимость формирования соответствующей новой записи в индексе на предыдущем уровне. Эта запись содержит новое значение ключа нового блока и указатель на его месторасположение. Процедура добавления такой записи аналогична описанной выше. Находится блок предыдущего уровня, куда должна быть помещена эта запись. Если в блоке есть пустое место, запись добавляется в блок, если блок полон, он делится на два блока, запись заносится в один из блоков, формируется запись индекса предыдущего уровня и т.д. Возможен вариант, когда придется делить блок самого верхнего уровня и формировать еще один уровень дерева. Рассмотрим для примера, изображенного на рис. 27, добавление записи с ключом 10.
2<10<43 Движение по левой ветви.
2<10<15 Движение по левой ветви.
2<8<10 Движение по правой ветви. Искомый блок
Он делится на 2 блока Сравнение 8<10<12. Запись с ключом 10 заносится в блок 1 На низшем уровне появилась новая запись с значением ключа 12. Необходимо добавление новой записи с ключом 12 и указателем на запись низшего уровня к индексу предыдущего уровня.
Сравнение 8<12. Запись добавляется во второй блок
2<8<15 Запись добавляется в блок 1
2<15<43 Запись с ключом 15 добавляется в первый блок
Полученная структура будет иметь вид, представленный на рисунке 9.8. 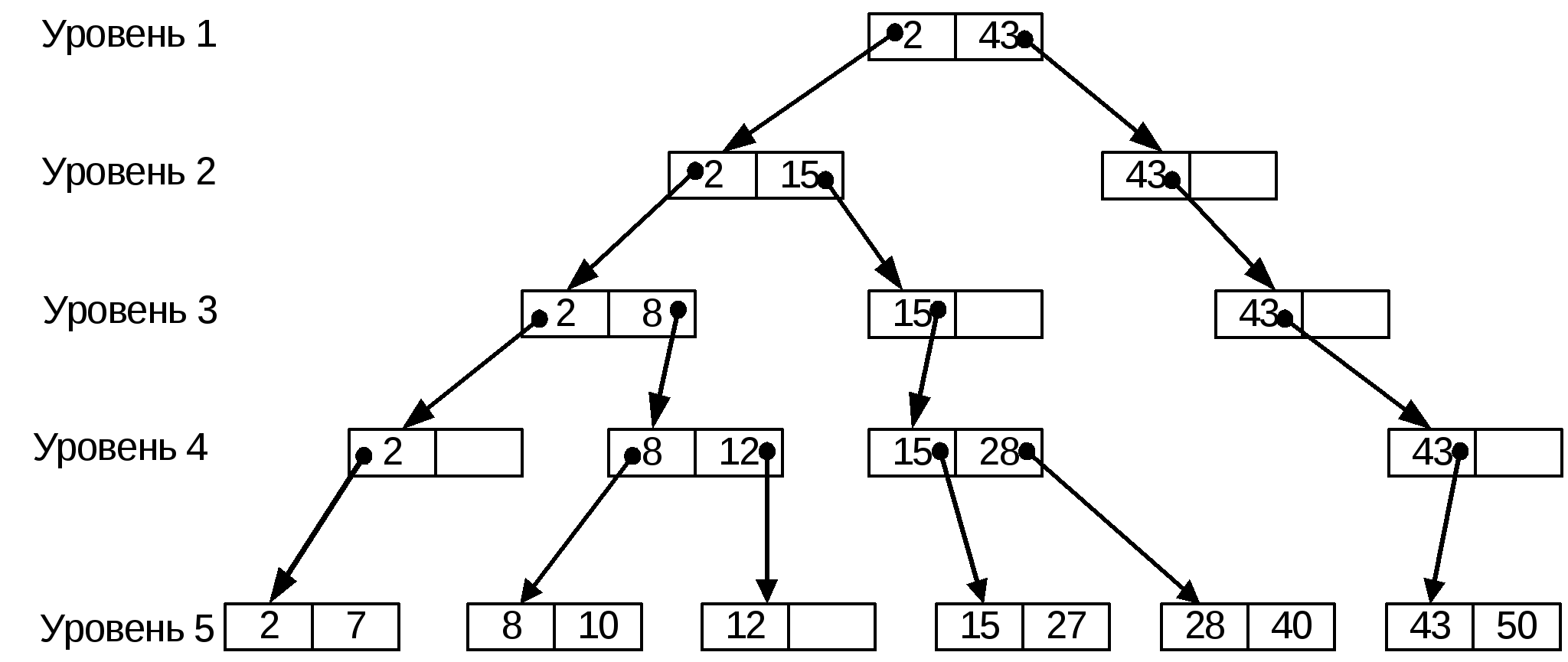 Рис. 9.8. В-дерево после добавления элемента Необходимо заметить, что используемый прием деления пополам полностью заполненного блока при добавлении в него записи приведет к тому, что блоки будут заполнены, в среднем, наполовину. Тогда процедура добавления записи будет существенно менее трудоемкой (если в нужном блоке есть место, запись добавляется в этот блок и вышестоящие уровни не перестраиваются). Структура хранения в виде B-дерева позволяет эффективно проводить операции поиска, чтения, удаления, модификации с оценкой числа обращений к внешней памяти числом уровней дерева l (l ≈ logkN), что существенно меньше числа обращений при переборе Процедура добавления записи тоже достаточно эффективна. Соответствующая структура хранения, в частности, используется в отечественной СУБД НИКА (ранее использовалась в системе ИНЕС) и на реальных задачах показала высокую эффективность. |
