Расчетно-экпериментальное обеспечение разработки реактивных ДМТ. В. И. Тимошенко, Ю. В. Кнышенко, М. И. Кошкин
 Скачать 1.84 Mb.
|
|
УДК 629.7.01 В.И. ТИМОШЕНКО, Ю.В. КНЫШЕНКО, М.И. КОШКИН РАСЧЕТНО-ЭКСПЕРИМЕНТАЛЬНОЕ ОБЕСПЕЧЕНИЕ РАЗРАБОТКИ РЕАКТИВНЫХ ДВИГАТЕЛЬНЫХ УСТАНОВОК МАЛОЙ ТЯГИ Предложена математическая модель системы жидкостных реактивных двигателей малой тяги, включающая расчетные модули течений компонентов топлива в питающих магистралях, динамики электроуправляемых топливных клапанов и термогазодинамических процессов в камерах сгорания. В совокупности со средствами стендовой отладки двигателей малой тяги, обеспечивающими верификацию результатов расчета, предлагаемое методическое обеспечение является важной составной частью при разработке, создании и эксплуатации жидкостно-реактивных систем управления движением космических аппаратов и последних степеней ракет-носителей A mathematical model of the system of liquid-propellant thrusters including design modules of propellant components flows in feed lines, the dynamics of electrically controlled propellant valves and thermogasdynamic processes in combustion chambers is proposed. The methodic support proposed is an important component in developing, creating and operating liquid-jet systems for controlling motion of spacecraft and launch vehicle final stages, along with means of thruster test bench for verification of calculation data. Ориентация и стабилизация космического аппарата (КА) в пространстве, коррекция его траектории, сближение и стыковка с другим космическим объектом, торможение, спуск и посадка, обычно обеспечиваются активными системами управления летательным аппаратом, исполнительными органами которых являются реактивные двигатели малой тяги (ДМТ). Эти двигатели применяются также в системах обеспечения повторных запусков маршевых ЖРД последних ступеней ракет-носителей (РН) с целью создания перегрузок, обеспечивающих безотрывное поступление жидких компонентов к заборным устройствам, спасения космических аппаратов при аварийном старте ракеты и др. Особенность систем управляющих ДМТ состоит в необходимости использования на всех этапах их разработки и функционирования математического моделирования течений в магистралях подачи компонентов топлива, в регулирующей аппаратуре, в камерах сгорания и сопловых устройствах в сочетании с результатами стендовой отработки и данными летных испытаний. В настоящей работе представлены основные составляющие математической модели системы ДМТ, порядок стендовой отработки и взаимодействие их в процессе разработки и эксплуатации. Количество двигателей и характер их размещения на КА и РН выбирается из условия обеспечения по каждой из осей управления требуемых моментов сил тяги, равных по величине и противоположных по направлению. На практике для этих целей, с учетом максимального быстродействия, резервирования и решения ряда других полетных задач, используется от 8 до 20 двигателей. В качестве рабочих тел ДМТ используются жидкие, твердые и газообразные топлива, а также газы, находящиеся в баллонах высокого давления или получаемые при возгонке сублимирующих веществ. Д В.И.Тимошенко, Ю.В.Кнышенко, М.И.Кошкин, 2005 Техн. механика. – 2005. – № 2. вухкомпонентные жидкостные реактивные двигатели малой тяги (ЖРДМТ), использующие, например, в качестве окислителя азотный тетраксид (АТ), а в качестве горючего несимметричный диметилгидразин (НМДГ), относятся к достаточно эффективным системам по суммарному импульсу и уровню тяги. Питание двигателей компонентами топлива осуществляется из собственных топливных баков, что обеспечивает высокую степень автономности их работы. Стремление снизить «сухую» массу ракеты-носителя при условии использования одинаковых компонентов топлива как для маршевого двигателя, так и для системы управляющих двигателей приводит к поиску технического решения, основанного на использовании для работы управляющих двигателей топливных баков маршевого двигателя. При этом открываются дополнительные возможности для повышения суммарного импульса тяги микродвигателей за счет значительно более полного использования, так называемых, «гарантийных остатков топлива» в топливных баках маршевого двигателя, в частности, для «пассивации» последних ступеней ракет-носителей (выработки остатков топлива, сброса газа из пневмосистем, увода ступени с траектории). Характерной особенностью таких систем ЖРДМТ является запаздывание включения и выключения двигателей по отношению к командным электрическим сигналам. Это обусловлено электрической и механической инерцией топливных клапанов [1–5]. В связи с этим, при больших интервалах между командными импульсными сигналами, каждое новое включение двигателя происходит в одинаковых условиях по массовому и тепловому состоянию в камере сгорания (КС). С уменьшением этих интервалов появляется связь между импульсами сначала по тепловому состоянию КС, а затем и по остаточной массе продуктов горения в КС. При этом большое значение имеет степень одновременности срабатывания клапанов окислителя и горючего, определяющая текущее соотношение компонентов топлива, поступающих в КС, от которого, в свою очередь, зависит полнота сгорания компонентов топлива и тяговые характеристики двигателя. Аналогичным образом на характер запуска двигателя влияют длины питающих магистралей. Волновые процессы в трубопроводах с жидкими компонентами имеют характерные времена, сопоставимые с временами функционирования управляющих двигателей. Это приводит к провалам в подаче компонентов в КС. Учитывая различие в длинах питающих трубопроводов окислителя и горючего, эти провалы могут вызвать большие колебания в соотношении компонентов, что может приводить либо к провалу тяги, либо к забросу давления в КС [5]. Особенности режимов работы (непрерывный, импульсный с различными сочетаниями включения, длительности импульсов и выключения), а также сложный пространственный характер топливных магистралей, изменяющийся в процессе работы (различное количество включаемых двигателей) и при переходе к многообразным модификациям РН и КА, предопределяют необходимость наличия математической модели, способной легко адаптироваться к любой конструктивной схеме управляющих двухкомпонентных двигателей и соответствующего стендового оборудования, обеспечивающего верификацию расчетных результатов. На различных этапах проектирования и эксплуатации управляющих двигателей используется различное расчетное и стендовое обеспечение. Рис.1 иллюстрирует взаимодействие математических моделей различного уровня и стендового методического обеспечения на основных этапах проектирования и эксплуатации управляющих двигателей, начиная от обоснования технического задания до летной эксплуатации. 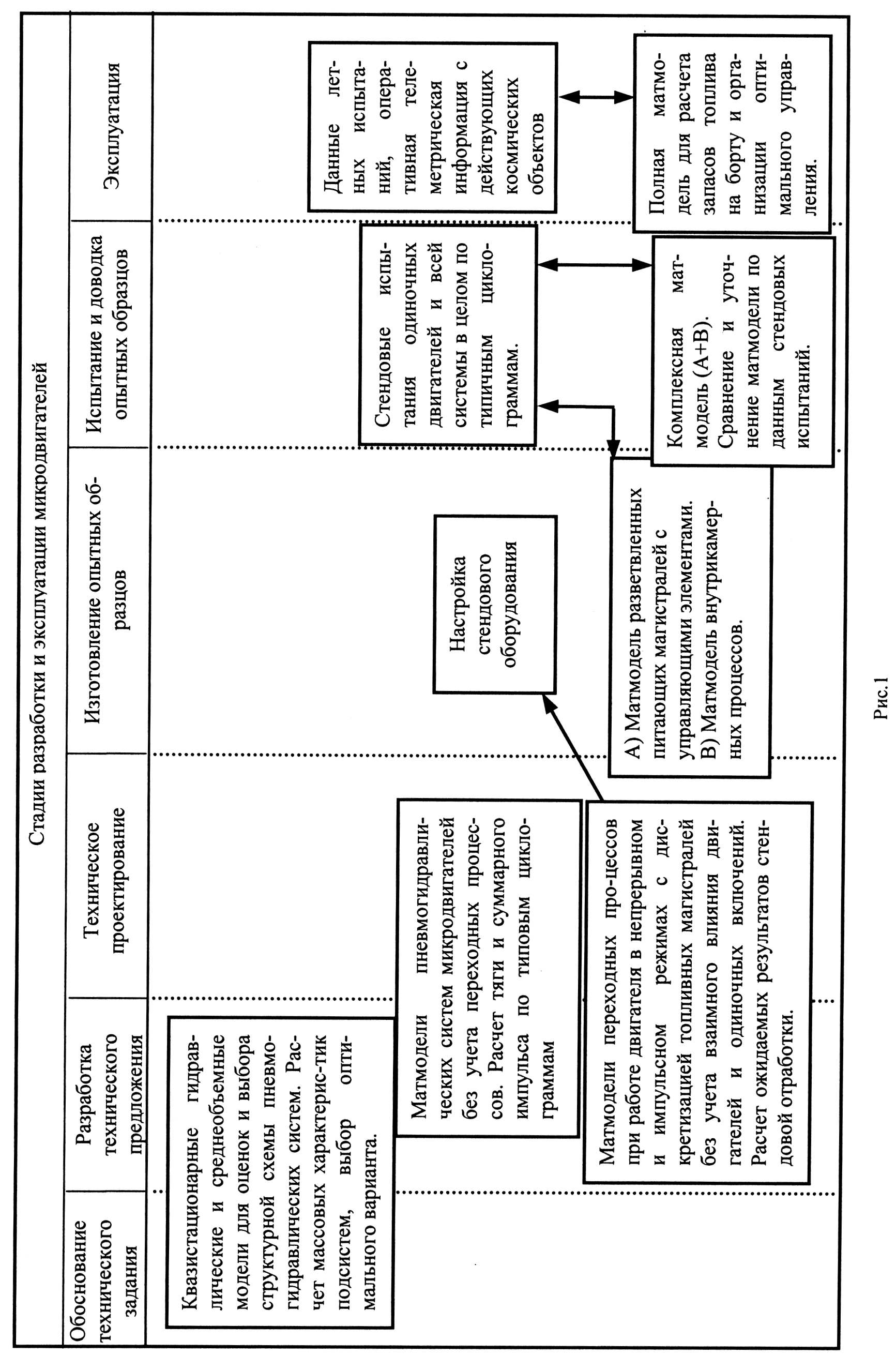 Методическое обеспечение, представляющее собой комплекс математических моделей отдельных систем и стендового оборудования, после уточнения по результатам летных испытаний, служит для сопровождения эксплуатации данной системы при расчете запасов топлива на борту и организации оптимального управления. Составными частями этого методического обеспечения являются: – математическая модель произвольной системы двигателей с учетом течений компонентов топлива по питающим магистралям; – математическая модель динамики электроуправляемых топливных клапанов; – математическая модель нестационарных течений в камерах сгорания с учетом конструктивных особенностей их исполнения и характера истечения продуктов горения из сопловых устройств; – методы стендовой отработки систем двигателей с моделированием основных рабочих режимов, позволяющие определить уровень совершенства конструкции, ресурсные возможности, эффективность средств контроля параметров системы в полете. В силу сложности рассматриваемой задачи при создании математических моделей и программного обеспечения широко используется метод расщепления по физическим процессам и геометрическим элементам и технология модульного программирования [6, 7]. Это позволяет создать унифицированный комплекс программ, который может использоваться при проектировании широкого класса систем управляющих двигателей малой тяги. Модель течений компонентов топлива в питающих магистралях. Для исследования течений в трубопроводной системе ее конструктивная схема должна быть подвергнута декомпозиции с выделением простых составных элементов. В общем случае система трубопроводов может быть представлена в виде набора простых трубопроводов (конструктивных участков), характеризующихся постоянными геометрическими параметрами (диаметром, толщиной стенки, материалом) и набора сингулярных элементов (емкостей, клапанов, тройников, теплообменных аппаратов и т.д.), которые могут трактоваться как сосредоточенные либо распределенные на некотором участке параметры. Подобное разделение составных элементов системы позволяет общую задачу расчета течений разбить на более простые задачи: задачу о течениях на конструктивных участках трубопроводов и задачу о течениях в сингулярных элементах. Решения этих задач в сечениях стыка составных элементов согласуется при помощи граничных условий, выражающих конкретные физические законы в этих сечениях. Течения сплошной среды в разветвленной трубопроводной системе рассматривается в гидравлическом приближении и описываются системой волновых уравнений для каждого из конструктивных участков трубопровода. Данная модель учитывает местные гидравлические сопротивления, возникающие на концах конструктивных участков. Для построения конечно-разностной сетки по координате и времени разветвленная пространственная трубопроводная система преобразуется к плоскому виду и представляется в виде матрицы  размерности n m. В этой матрице на местах элементов, соответствующих расчетным точкам трубопровода, стоят номера этих точек. Нумерация их может быть произвольной, но упорядоченной в пределах каждого из внутренних конструктивных участков.В зависимости от значений элементов матрицы, находящихся в окрестности расчетной точки, она классифицируется либо как регулярная (находящаяся внутри конструктивного участка), либо как граничная или сингулярная (выход из бака, вход в камеру сгорания двигателя малой тяги, сечение тупикового трубопровода, стык трубопроводов, клапан, жиклер и др.) Течение каждого из компонент топлива в питающих трубопроводах описывается следующей системой уравнений 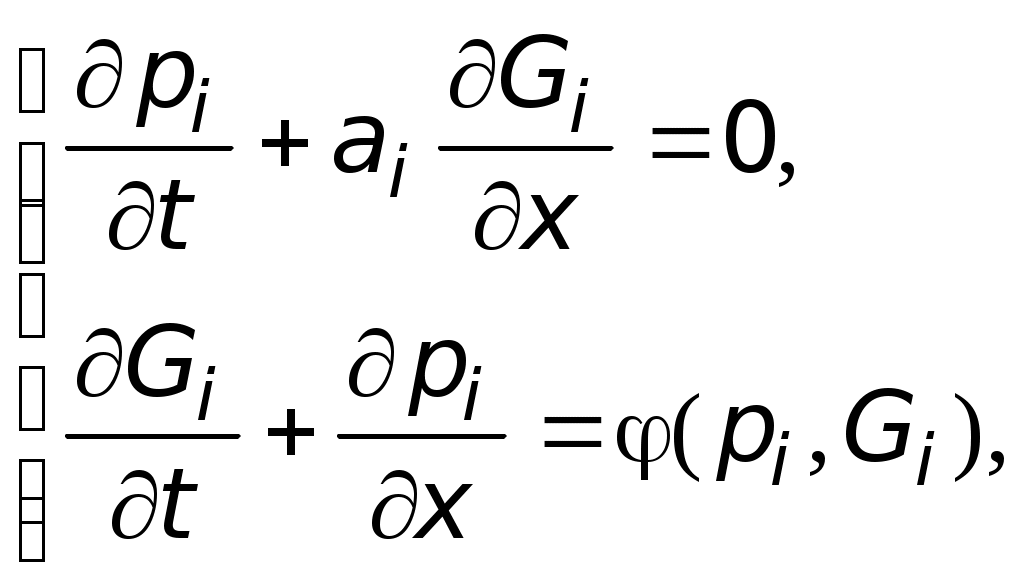 (1)где  – координата по длине конструктивного участка трубопровода;  – номер участка; – давление в сечении на -ом участке; – плотность потока массы в сечении на -ом участке;  –плотность и скорость жидкости в сечении на -ом участке соответственно;  – скорость распространения возмущений (скорость звука).Функция  имеет вид где  – коэффициент гидравлического сопротивления на i-ом участке;  –диаметр трубопровода на i-ом участке.Скорость звука на каждом из конструктивных участков зависят от формы поперечного сечения трубопровода, толщины стенки, материала, плотности и коэффициента сжимаемости жидкости. Решение системы (1) проводится при соответствующих начальных условиях. При пуске системы и выходе ее на установившийся режим принимаются нулевые значения расходов и постоянные значения давлений во всех расчетных точках. При полном (частичном) останове системы или изменении структуры трубопроводной сети в качестве начального режима течения принимается стационарный режим с соответствующим распределением давлений и расходов во всех расчетных точках. Интегрирование системы (1) осуществляется методом характеристик. Расчетная сетка для численного интегрирования имеет постоянный шаг по координате и времени. Величина шага по координате выбирается, исходя из длины наименьшего участка. Коэффициенты гидравлических потерь по длине каждого из конструктивных участков в квазистационарном приближении для гидравлически гладких труб определяются в зависимости от величины числа Рейнольдса в расчетных узлах по формулам Пуазейля (при  ) или Блазиуса (при  ) [4].Решения, получаемые на конструктивных участках трубопроводов должны быть согласованы с решениями, найденными в сингулярных узлах. Такое согласование осуществляется на основе использования балансовых соотношений для расходов, скоростей, давлений и соотношений на характеристиках, исходящих из ближайших узлов на конструктивных участках, примыкающих к сингулярным узлам. Некоторые конкретные варианты таких соотношений приведены ниже. Для конечной расчетной точки тупикового трубопровода (участок трубопровода с выключенным двигателем малой тяги) значения 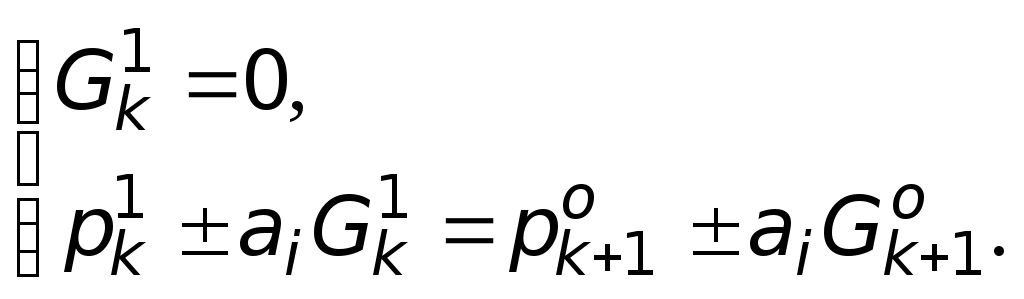 и  находятся из следующих соотношений: Для определения 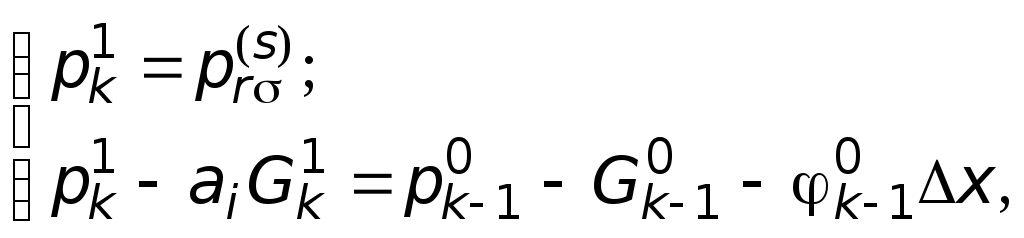и на стыке трубопроводов с источниками давления используется условие равенства давления в данной расчетной точке давлению на выходе из источника давления и условие на характеристике отрицательного наклона: где  – давление в  -ом источнике давления.На стыке трубопроводов (не более четырех) в узловой точке должно выполняться условие равенства расходов жидкости, приходящих в узел и истекающих из него. Без учета местных потерь в узле соблюдается равенство давлений во всех граничных точках стыкуемых трубопроводов. При наличии местных сопротивлений их величина должна быть учтена в зависимости от направления течения и геометрических характеристик трубопроводов в узле. Поэтому на стыке трубопроводов подобного типа для каждого из них должен быть определен свой коэффициент местного гидравлического сопротивления. Для нахождения значений коэффициентов местных потерь могут быть использованы методы, известные в гидравлике [8]. Ниже, в качестве примера, приведены расчетные зависимости для стыка двух трубопроводов. Перед расчетом параметров на стыке трубопроводов (не более четырех) в узлах расчетной сетки перед и за стыком необходимо задать первоначальное направление потока: если поток направлен к стыку, то признак направления  присваивается точке перед стыком; если от стыка, то значение  присваивается точке за стыком. При стыке двух трубопроводов возможны два варианта:  ,  ,  или  ,  , .Для первого варианта система уравнений для определения давления и массовой скорости в точках  и  будет состоять из условия на положительной характеристике (для  ), соотношения для местного сопротивления, баланса расхода в стыке и условия на отрицательной характеристике ( ) (2)где  ,  – площади проходных сечений трубопроводов на стыке;  = – коэффициент, характеризующий местное гидравлическое сопротивление стыка при данном направлении потока.Из системы (2) итерационным путем находятся  ,  ,  и  . Аналогично могут быть получены соотношения для второго варианта и стыка трех трубопроводов.Граничное условие на выходе из трубопроводной системы определяется параметрами в камере сгорания и гидравлическими сопротивлениями на конце выходного трубопровода. Для определения  и  имеем условие для давления и соотношение на характеристике положительного наклона: где  – давление в данной камере сгорания в каждый момент времени;  – местное сопротивление на выходе из трубопровода.Величина давления изменяется от  в момент открытия топливных клапанов двигателя до значений  . На стационарном режиме величина  также принимает некоторое постоянное значение.Динамика топливных электроуправляемых клапанов. Одним из средств управления потоками жидкости в системах двигательных установок являются клапаны. Клапаны применяются для открытия и закрытия прохода рабочего тела в магистрали, в которой они установлены. При срабатывании клапана его детали, закрывающие или открывающие проходное сечение, перемещаются из одного фиксированного положения в другое. Срабатывание может быть однократным или многократным. Управляющие воздействия на клапан могут быть различной природы: пневматические, гидравлические, электрические, комбинированные. В системах жидкостных реактивных двигателей малой тяги (ЖРДМТ) чаще всего используются электрические командные сигналы, обеспечивающие срабатывание электромагнита, усилие которого преодолевает сопротивление пружины, прижимающей тарель клапана к седлу. Рассмотрим работу топливного электроуправляемого клапана. Схематически он представлен на рис. 2. Процесс полного открытия клапана можно разделить на три этапа. Первый этап, от момента времени  (замыкание цепи обмотки электромагнита 1) до начала трогания якоря 2, характеризуется нарастанием тока в обмотке электромагнита до такой величины, при которой сила тяги электромагнита станет больше сил сопротивления пружины 3 и перепада давления на клапане 4.Интервал времени от подачи напряжения на обмотку до трогания якоря называется временем трогания. Второй этап характеризует движение якоря до упора (полное открытие клапана). Клапан, жестко связанный с якорем, отходит от седла 5, открывая проход для подачи жидкости (компонента топлива) в камеру сгорания. Суммарное время первого и второго этапов является временем срабатывания (открытия) клапана. Третий этап характеризует выход электрических и магнитных параметров электромагнитного клапана на стационарные значения (положение якоря на упоре). Для цепи обмотки электромагнита справедливо уравнение [3, 9]  (3)где  – электрическое напряжение, подаваемое на обмотку электромагнита;  – ток в обмотке электромагнита;  – омическое сопротивление обмотки;  – индуктивность обмотки;  – время.На первом этапе, до момента трогания, якорь неподвижен и зависимость индуктивности от тока слаба, поэтому можно считать, что  , следовательно  .С учетом начального условия  решение уравнения (3) имеет вид , (4)где  .По зависимости (4) ток в обмотке электромагнита будет изменяться до момента трогания якоря. Ток трогания якоря  определяется из условия равенства силы тяги электромагнита  и сил механического противодействия (упругости пружины, трения, перепада давления)   при максимальном зазоре между якорем и ярмом электромагнита  (см. рис.2).Тяговое усилие электромагнита определяется выражением [3]  . Сила механического противодействия представляет собой сумму силы упругости пружины и силы давления жидкости на клапан  , где  – жесткость возвратной пружины клапана;  – начальное сжатие пружины;  – давление подачи жидкости;  – площадь седла.На втором этапе, при движении якоря, необходимо учитывать, что индуктивность обмотки электромагнита L изменяется по мере уменьшения зазора между якорем и ярмом в соответствии с зависимостью  , где  – магнитная проницаемость вакуума;  – площадь якоря электромагнита;  – число витков катушки электромагнита;  – текущий зазор между якорем и ярмом электромагнита; отсчет ведется от закрытого положения клапана и предварительно сжатой пружины на величину .Для определения величины тока, тяговых усилий, пути и скорости движения якоря необходимо совместно с уравнением (3) решать уравнение движения якоря  ,где  – масса подвижных частей электромагнитного клапана;  – тяговое усилие электромагнита; – суммарная сила механического противодействия (сила упругости пружины, сила вязкого трения, сила давления жидкости на клапан).Сила  определяется , где  – коэффициент вязкого трения;  – скорость.Система уравнений второго этапа включения электромагнитного клапана имеет вид  Решение данной системы дифференциальных уравнений необходимо получать при следующих начальных условиях:  ,  ,   до выполнения условия  , что соответствует достижению якорем упора. С этого момента начинается третий этап срабатывания электромагнитного клапана на открытие.Данный этап характеризуется постоянством зазора между якорем и ярмом электромагнита. Процесс сопровождается нарастанием тока в обмотке и выходом его на стационарное значение, равное  . Темп выхода на стационарный уровень отличается от темпа выхода тока на первом этапе. С одной стороны, вследствие притяжения якоря и уменьшения зазора, индуктивность имеет максимальное значение, определенное в конце второго этапа. С другой стороны, на данном этапе рост тока вызывает насыщение магнитопровода, что приводит к снижению индуктивности. Как показывают опыты [9], результирующей этих факторов является уменьшение индуктивности. Сила тяги электромагнита определяется аналогично первому этапу. Процесс закрытия клапана можно также разделить на три этапа. Первый этап, от момента времени  (снятие напряжения с цепи обмотки электромагнита с одновременным шунтированием ее некоторым омическим сопротивлением [3]) до начала отпускания якоря, характеризуется падением тока в обмотке электромагнита до такой величины, при которой суммарная сила тяги электромагнита и перепада давления на клапане станет меньше силы упругости возвратной пружины. Интервал времени от снятия напряжения с обмотки до начала движения якоря называется временем залипания якоря.Второй этап характеризует движение якоря до посадки клапана на седло (полное закрытие клапана). Клапан, жестко связанный с якорем, полностью закрывает проход для подачи жидкости (компонента топлива) в камеру сгорания. Суммарное время первого и второго этапов является временем отпускания (закрытия) клапана. Третий этап характеризуется выходом электрических и магнитных параметров электромагнитного клапана на нулевые значения (клапан находится на седле). Для описания процессов в обмотке электромагнита на первом этапе закрытия клапана также используется уравнение (3), в котором необходимо положить  . При этих условиях решение уравнения (3) будет иметь вид , где  – электрическое сопротивление, шунтирующее обмотку электромагнита при закрытии клапана;  – установившееся значение тока при полностью открытом клапане; если напряжение снимается с обмотки в момент времени, когда ток в обмотке после открытия клапана еще не вышел на стационарное значение, в качестве принимается мгновенное значение тока.Тяга электромагнита на первом этапе закрытия будет изменяться по зависимости, соответствующей третьему этапу открытия клапана.При снижении тяги электромагнита до величины, меньшей суммарной силы противодействия пружины и перепада давления на клапане, начинается второй этап закрытия клапана, характеризующийся движением якоря и посадкой клапана на седло. Система уравнений второго этапа закрытия клапана имеет вид 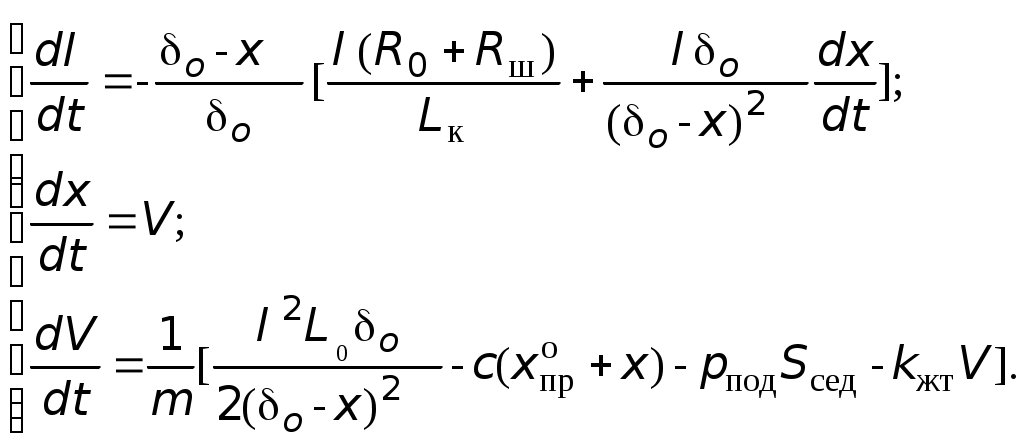 Решение данной системы должно быть получено при следующих начальных условиях:  до выполнения условия  , что соответствует посадке клапана на седло. Третий этап срабатывания электромагнитного клапана на закрытие характеризуется постоянством зазора между якорем и ярмом электромагнита, который является максимальным. Процесс сопровождается дальнейшим спадом тока в обмотке и выходом его на нулевое значение. Для данного этапа решение уравнения (3) при  и начальном условии  , имеет вид , где  – время окончания второго этапа закрытия (посадка клапана на седло);  – ток в обмотке электромагнита в конце второго этапа.Тяговое усилие электромагнита определяется аналогично первому этапу открытия клапана. Модель процессов в камерах сгорания. Для математического описания процессов, протекающих в камере сгорания используются среднеобъемные и континуальные модели [5]. При использовании среднеобъемной модели принимается допущение, что время от момента впрыска топлива до мгновенного превращения его в продукты реакции (время запаздывания  ) считается постоянным и зависит от параметров камеры сгорания. Такое допущение позволяет рассматривать камеру сгорания как объем, наполненный газом, в котором в течение времени к в виде капель находится впрыснутое топливо [3]. Полагается также, что продукты реакции топлива являются идеальным газом, температура, давление и газовая постоянная которого одинаковы как вдоль камеры, так и по ее радиусу. Уравнение баланса массы в камере в каждый момент времени  (5)где  – скорость накопления массы  газообразных продуктов реакции;  – массовый приход газа в камеру;  – массовый расход из камеры.Расход газа из камеры сгорания определяется из соотношения  (6)где   – давление в камере сгорания;  – площадь критического сечения сопла;  – газовая постоянная и температура продуктов реакции соответственно.Уравнение состояния продуктов горения в камере сгорания  , (7)где  – объем камеры сгорания.Работоспособность продуктов реакции  является функцией коэффициента  и . На практике, в большинстве случаев, зависимость от можно не учитывать [3]. Считая зависимость от k известной и кусочно-постоянной на временном шаге численного решения системы (1) с учетом (6), (7) и Gпр() = G0(-k) + Gк(-k), уравнение (5) принимает вид (8)где  .С приемлемой для практики точностью время запаздывания пропорционально приведенной длине камеры сгорания L(L=Vк /Fkр). Для камер сгорания управляющих двигателей  составляет величину порядка десятитысячных долей секунды.Найденное значение путем численного интегрирования уравнения (8) на интервале времени, равном шагу по времени в методе характеристик, используется в качестве граничного условия на выходе из трубопроводной системы для задачи о движении компонентов топлива в подводящих магистралях.При работе камеры сгорания в импульсном режиме, когда длительность подачи компонентов может быть сопоставима со временем движения компонентов топлива по длине камеры сгорания и сопла необходимо использовать модель КС и сопла с распределенными параметрами [10]. Тестовые результаты расчетов и данные стендовой отработки двигателя малой тяги. Волновые уравнения для питающих магистралей, уравнения динамики клапанов и уравнения, описывающие газодинамические процессы в камерах сгорания (в среднеобъемной или распределенной постановках) представляют собой замкнутую систему, которая позволяет моделир  овать работу системы управляющих двигателей по любым циклограммам. Алгоритм решения данной задачи реализован в виде комплекса программ на алгоритмических языках ФОРТРАН и ПАСКАЛЬ. В качестве иллюстрации изложенной выше методики приведены результаты расчетов двухкомпонентной системы управляющих двигателей, применяемой на последней ступени РН «Циклон». На рис.3 представлена схема двухкомпонентной системы управляющих двигателей, состоящая из баллона со сжатым газом 1, баков горючего 2 и окислителя 3, коллекторов горючего 4 и окислителя 5, и двигателей 6. На рис.4 представлена схема подачи окислителя «О» и горючего «Г» в камеру сгорания двигателя малой тяги. Н  а рис. 5 приведены результаты расчета давлений в камерах сгорания при запуске и выходе на установившийся режим трех двигателей со сдвигом во времени. После запуске одного двигателя тягой 100 Н (кривая 1), примерно через 0,03 с происходит почти одновременный запуск двух двигателей тягой 30 Н (кривые 2 и 3). Приведенные данные иллюстрируют взаимное влияния двигателей. Так, при включении двух двигателей тягой 30 Н давление в камере сгорания двигателя тягой 100 Н падает на 10 – 12 %, а затем через 0,015 с выходит на прежний установившийся уровень.Для верификации математических моделей и подтверждения правильности принятых проектных и конструкторских решений при разработке двигательной установки и отдельных ее узлов проводятся ее испытания на стендовом оборудовании в наземных условиях. С  целью максимального приближения стендовых условий к реальным испытания на штатных компонентах ракетного топлива проводятся в барокамере, в которой поддерживается давление на момент первого включения порядка 0,01 – 0,1 Па, а во время работы – не выше давления, обеспечивающего безотрывное истечение продуктов сгорания из сопел двигателя малой тяги. Эвакуация продуктов сгорания обеспечивается специальными откачивающими системами. Это позволяет оценить такие характеристики работы двигателя малой тяги, как: время открытия клапанов с момента подачи команды на включение двигателя до полного открытия клапана ЭГК; время закрытия клапанов; разновременность открытия клапанов «О» и «Г»; разновременность закрытия клапанов «О» и «Г»; время с момента подачи команды на открытие клапанов (включение двигателя) до набора двигателем 90 % тяги; время с момента подачи команды на закрытие клапанов (выключение двигателя) до спада тяги до 10 % от номинала. Указанные параметры задаются техническим заданием на разработку двигателя малой тяги. Н  иже приведены результаты стендовой отработки одиночного двигателя. Общая схема измерений параметров при стендовой отработке представлена на рис.6. В процессе работы двигателя на стенде производилась запись во времени следующих параметров: напряжения , подаваемого на обмотки электроуправляемых топливных клапанов, тока , протекающего по этим обмоткам, давлений  и расходов поступающих в двигатель компонентов топлива  , давления в камере сгорания двигателя  , давления на срезе сопла при работе двигателя  , температуры форсуночной головки  , стенки камеры сгорания  и среза сопла. Данная отработка проводилась на стадиях разработки и совершенствования этих двигателей.У   Рис. 7 словия работы одиночного двигателя на стенде существенным образом отличались от условий его работы в реальной системе двигателей (по длинам подводящих трубопроводов, их диаметрам, наличию дополнительных демпферов). Отбор давления из камеры сгорания на датчик давления производился из объема охлаждающей рубашки, что приводило к сглаживанию на осциллограмме пиков давления при запуске двигателя. На рисунке 7 приведены результаты расчета одиночного импульса тяги: давления в камере сгорания и тока, протекающего по обмоткам топливных клапанов – кривые 1 и 3. Там же показаны изменения этих параметров, полученные по результатам стендовых испытаний одиночного двигателя соответственно кривые 2 и 4. Приведенные данные показывают, что характер изменения давления в камере сгорания и тока поступающего на обмотки электроуправляемых клапанов, полученный расчетным путем, качественно согласуется с экспериментальными данными. Количественные расхождения в характере изменения тока, что связанно с некоторой неопределенностью в исходных данных по электроуправляемым клапанам, свидетельствуют о необходимости уточнения расчетных моделей, в первую очередь, путем уточнения исходных данных при проведении стендовой отладки. Таким образом, предлагаемое расчетно-методическое обеспечение при наличии необходимого стендового оборудования позволяют в комплексе ставить и решать задачи разработки и создания двигательных установок малой тяги, отвечающие современным требованиям. 1. Кокорин В.В., Рутовский Н.Б., Соловьев Е.В. Комплексная оптимизация двигательных установок систем управления. – М.: Машиностроение, 1983.– 184с. 2. Гришин С.Д., Кокорин Н.П., Харламов Н.П. Теоретические основы создания двигательных установок для управления космическими аппаратами. – М.: Машиностроение, 1985.– 192с. 3. Беляев Н.М., Белик Н.П., Уваров Е.И. Реактивные системы управления космических летательных аппаратов.- М.: Машиностроение, 1979.– 232с. 4. Кнышенко Ю.В. Математическая модель течений сплошной среды в разветвленных трубопроводных системах // Всеукраїнська наукова конференція (23-25 квітня 2001 р.) “Математичні проблеми технічної механіки”: Тези доповідей.– Дніпродзержинськ, 2001.– С.48. 5. Timoshenko V.I., Koshkin M.I., Knyshenko J.V. Methodical support of development of increased safe life propulsion systems of a small thrust // 52nd International Astronautical Congress 1-5 Oct. 2001.– Toulouse, France, 2001. 6. Тимошенко В.И., Лиманский А.В. Технология численного решения на ЭВМ задач газовой динамики. – К.: Наукова думка, 1985. – 232с. 7. Тимошенко В.И. Газовая динамика высокотемпературных технологических процессов – Днепропетровск: Институт технической механики НАНУ и НКАУ, 2003. – 460 с. 8. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 559 с. 9. Рабинович Л.В. Электроавтоматика авиационных электромеханических установок.– М.: Оборонгиз, 1957.– 422с. 10. Дегтяренко В.И. Упрощенная математическая модель нестационарных газодинамических процессов в камерах сгорания двигателей малой тяги // Техническая механика. – 2003. – № 1. – C. 74–81. Ин-т техн. механики НАН Украины и НКА Украины, Получено 07.10.05, Днепропетровск, в окончательном варианте 10.10.05 Государственное конструкторское бюро «Южное», Днепропетровск |