МОА_вопросы к экзаменам (1). В каждом билете три вопроса два теоретических и одна задача

• Название: В каждом билете три вопроса два теоретических и одна задача
• Дата: 02.03.2023
• Размер: 4.85 Mb.
• Имя файла: МОА_вопросы к экзаменам (1).docx
• Тип: Задача; #963851

В каждом билете три вопроса: два теоретических и одна задача.

1. 
   Определение дифференциального уравнения первого порядка, его общего и частного решения, общего интеграла.
   

Линейным дифференциальным уравнением первого порядка называется такое дифференциальное уравнение, в которое неизвестные функции y и y′ входят в первых степенях и не перемножаются между собой.

Общим решением уравнения называется множество всех его решений. Общее решение зависит от одной произвольной постоянной C и определяется формулой:



Любое конкретное решение y = y (x) (решение задачи Коши) уравнения 1го порядка, называется частным решением уравнения

Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. Если общее решение задано неявно соотношением: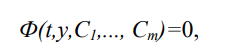



то называется общим интегралом уравнения

2. 
   Геометрический смысл общего и частного решения дифференциального уравнения.
   

Геометрический смысл дифференциального уравнения заключается в том, что оно устанавливает зависимость между координатами точек интегральной кривой и значением производной, то есть в каждой точке определяется направление касательной к искомой интегральной кривой. Таким образом, уравнение определяет поле направлений, и задача интегрирования дифференциального уравнения заключается в том, чтобы найти кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Каждая из интегральных кривых представляет собой график решения исходного дифференциального уравнения. Найти решение уравнения с начальным условием геометрически означает выделение из множества интегральных кривых той кривой, которая проходит через точку  . Всё множество интегральных кривых представляет общее решение дифференциального уравнения.

3. 
   Задача Коши для дифференциального уравнения первого порядка, геометрический смысл.
   

Геометрический смысл задачи Коши, заключается в том, чтобы во множестве всех интегральных кривых системы найти ту, которая проходит через точку (t0, x0)

ИЛИ

Для дифференциального уравнения 1-го порядка начальные условия имеют вид пары чисел (x0; y0). Тем самым ставится задача отыскания решения y(x), для которого y(x0) =y0. Геометрически это означает выбор из совокупности интегральных кривых той, которая проходит через заданную точку плоскости

4. 
   Определение линейного однородного дифференциального уравнения n-ого порядка.
   

Линейным однородным уравнением n−го порядка с постоянными коэффициентами называется уравнение вида:





Общее решение уравнения представляет собой линейную комбинацию частных решений, образующих фундаментальную систему
5 Конечная разность Разностное уравнение.

Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании.



Разностное уравнение — уравнение, связывающее значение некоторой неизвестной функции в любой точке с её значением в одной или нескольких точках, отстоящих от данной на определенный интервал. Применяется для описания дискретных систем.
6. Определение линейного неоднородного дифференциального уравнения n-ого порядка.

Неоднородное дифференциальное уравнение — дифференциальное уравнение (обыкновенное или в частных производных), которое содержит не равный тождественно нулю свободный член — слагаемое, не зависящее от неизвестных функций.

7. Характеристическое уравнение линейного однородного дифференциального уравнения 2-ого порядка.

y'' + p(x)y' + q(x)y = f(x),

8. Общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения.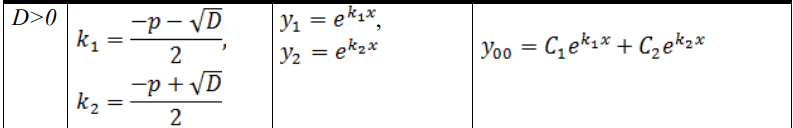



9. Общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения.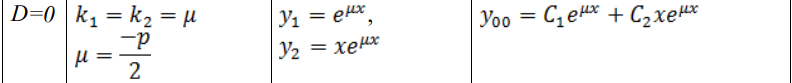


10. Общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения.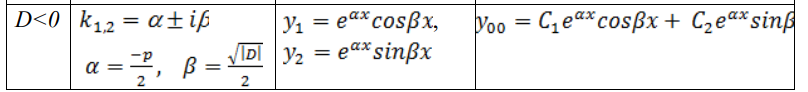


11. Метод подбора частного решения линейного неоднородного дифференциального уравнения.




12. Как составляется общее решение линейных неоднородных дифференцильных уравнений.





13. Определение системы линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами.


14. Нормальный вид системы дифференциальных уравнений первого порядка.

15. Сведение системы двух линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами к одному линейному дифференциальному уравнению второго порядка.

16. Преобразование системы линейных дифференциальных уравнений к матричному виду. Вектор внешних воздействий.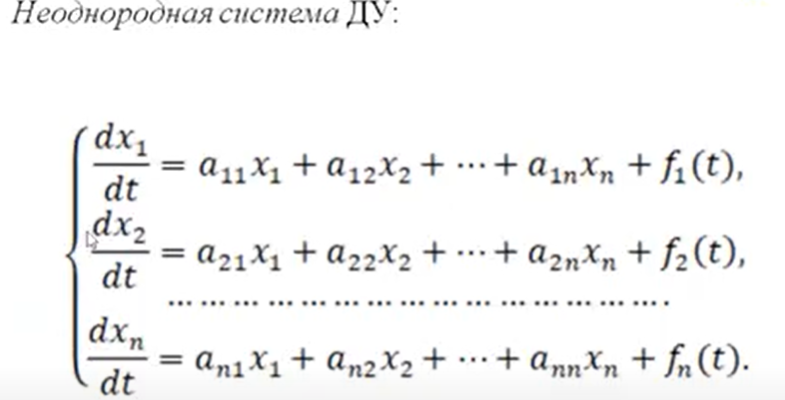










17. Определение преобразования Лапласа. Свойства преобразования Лапласа (теоремы).

18. Приведение дифференциальных уравнений и систем ДУ в операторный вид с помощью преобразования Лапласа.

19. Необходимость численного решения дифференциальных уравнений. Методы Эйлера и Рунге-Кутта.

20. Аксиоматическое и классическое определение вероятности.





21. Геометрическое и статистическое определение вероятности.







22 Формулы сложения и умножения вероятностей.


23. Определение случайной величины. В чем отличие между дискретной и непрерывной случайной величиной?


24. Дайте определение закона распределения случайной величины



25. Дайте определение функции распределения вероятностей.



26. Дайте определение плотности функции распределения непрерывной случайной величины.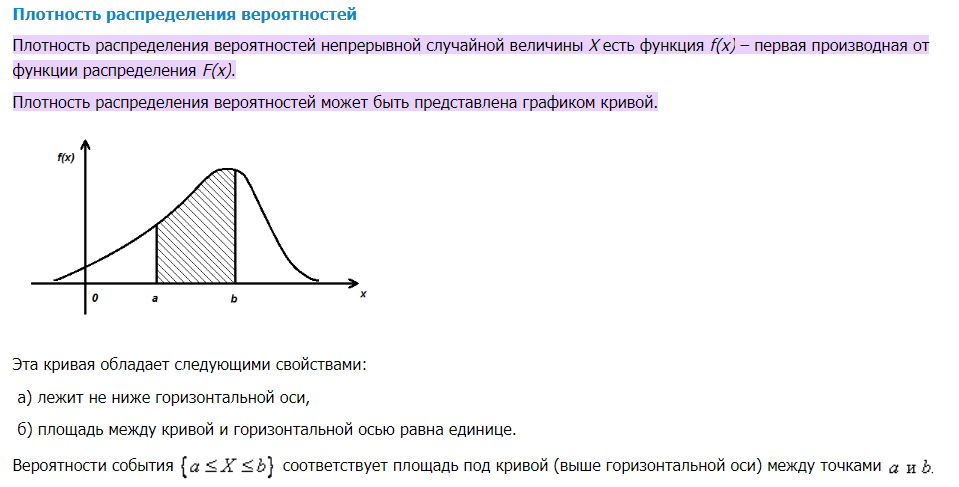


27. Для каких случайных величин можно постоить интегрельную и дифференциальную функции распределения:

С увеличением x функция распределения «накапливает» (суммирует) вероятности, а значит, является неубывающей и изменяется в пределах 0 ≤ 𝐹(𝑥) ≤ 1. По этой причине функцию распределения любой непрерывной случайной величины называют интегральной функцией распределения. Функция распределения любой непрерывной случайной величины всегда и всюду непрерывна.
Площадь гистограммы равна единице. Гистограмма составляется для интервальных рядов. Гистограмма - статистический аналог функция плотности распределения непрерывной случайной величины (дифференциальной функции распределения).

Если не непрерывные случайные величины
28 Числовые характеристики случайных величин.

Полными характеристиками случайных величин являются их функции распределения или плотности распределения вероятностей.
Числовые характеристики можно условно подразделить на характеристики положения (математическое ожидание, мода, медиана, квантиль), характеристики рассеяния (дисперсия, среднее квадратическое отклонение), характеристики формы (асимметрия, эксцесс). Одной из наиболее важных числовых характеристик случайной величины является ее среднее значение, называемое также математическим ожиданием.
29. Определение математического ожидания случайной величины. Формулы вычисления. Что характеризует эта величина?


Вероятностный смысл математического ожидания дискретной случайной величины, возможные значения которой получены при большом числе опытов, состоит в том, что оно приближенно равно среднему арифметическому наблюдаемых значений (или среднее арифметическое наблюдаемых значений приближается к математическому ожиданию при неограниченном увеличении числа испытаний).
Математическое ожидание случайной величины X (обозначается M(X) или реже E(X)) характеризует среднее значение случайной величины (дискретной или непрерывной).

30. Определение дисперсии случайной величины. Формулы вычисления. Что характеризует эта величина?





31. Определение среднего квадратического отклонения. Формулы вычисления. Что характеризует эта величина?



Среднее квадратическое отклонение характеризует разброс значений относительно среднего (математического ожидания).

32 Как находится вероятность попадания случайной величины Х в интервал (a;b)?




33 Как строится график функции распределения случайной величины?

Иногда распределение случайной величины Х изображают в виде графика, по оси абсцисс которого откладывают возможные значения 𝑥_i , а по оси ординат – вероятности 𝑝_i
34 Как находится вероятность того, что значение случайной величины будет найдено с ошибкой, не превосходящей по абсолютной величине ?


35. Дайте определения: генеральной и выборочной совокупности (выборки), объёма выборки, варианты.

На основе знания некоторых свойств элементов, полученных из определенного множества, Задача математической статистики – высказать утверждения о свойствах некоторой совокупности, называемой генеральной совокупностью на основании знания свойств элементов, полученных из этой совокупности. В генеральной совокупности обычно требуется признание какого-то свойства, которое зависит от случайности и носит качественный или количественный характер.
Генеральная совокупность — это вся совокупность объектов, подлежащих изучению.
Набор объектов, выбранных случайным образом из генеральной совокупности, называется выборочным набором или выборкой. Другими словами – это элементы, подлежащие изучению. Количество элементов выборки называется ее объемом. Выборочный метод заключается в том, что из генеральной совокупности выбираются N объектов, которые лучше его характеризуют. Если выборка дает достаточное представление об особенностях генеральной совокупности, то она репрезентативна (т. е. верно указывает пропорции генеральной совокупности).

36 Дайте определение оценки параметра генеральной совокупности. В чем отличие оценки от самого оцениваемого параметра?
В математической статистике для статистических распределений вводятся характеристики, аналогичные числовым характеристикам теоретических распределений, которые называются параметрами генеральной совокупности: математическое ожидание, дисперсия, модой, медиана и т.д.
Вычисленные же по результатам наблюдений приближенные значения параметров называются числовыми оценками параметров или просто оценками.
Для параметров генеральной совокупности и их оценок вводятся разные обозначения: например, если параметр обозначен 𝜃, то его оценка обозначается 𝜃෠. Значение параметра, вычисленное по ограниченному объему экспериментальных данных, является случайной величиной, т. е. значение такой величины от выборки к выборке может меняться заранее непредвиденным образом. Следовательно, в результате обработки экспериментальных данных, определяется не значение параметра 𝜃, а только лишь его приближенное значение 𝜃෠ – статистическая оценка параметра.
Чаще всего параметры генеральной совокупности обозначаются греческими буквами, соответствующие выборочные значения параметров обозначаются латинскими буквами.

37 Как построить дискретный вариационный ряд?

Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант  (значений величины  ) и соответствующих им частот либо относительных частот.

Относительные частоты рассчитываются по формулам:

, где   – объем выборки, при этом, сумма всех относительных частот:  .
38. Как построить интервальный статистический ряд?

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов.
Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.
Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:



Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы:

После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
  ден. ед. – хорошим тоном считается указывать размерность.

Вычислим размах вариации:
 ден. ед. – длина общего интервала, в пределах которого варьируется цена.

Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса: 

, где   – десятичный логарифм* от объёма выборки и   – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

* есть на любом более или менее приличном калькуляторе

В нашем случае получаем:
 интервалов.

Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
 – длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»:  . Посему от самой малой варианты   отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по  , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины   (например,  ) – они требуются почти во всех тематических задачах:




– убеждаемся в том, что самая большая варианта   вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем:



Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.

Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна:   – и её нужно причислить к интервалу  .

В результате получаем интервальный вариационный ряд:



при этом обязательно убеждаемся в том, что ничего не потеряно:


Изобразим ряд графически. Для этого по каждому интервалу нужно найти (не пугаемся): плотность частот  , относительные частоты   (округляем их до 2 знаков после запятой), а также плотность относительных частот  . Поскольку длина частичного интервала  , то вычисления заметно упрощаются.
39 Что такое гистограмма частот и относительных частот?

Гистограмма частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям частот:



Площадь гистограммы частот в точности равна объёму совокупности:  .  В нашем случае   и плотности   совпали с самими частотами  , таким образом: 
Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям относительных частот:


Площадь такой гистограммы равна единице:  , и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.
40 Определение полигона частот и относительных частот.

И для ИВР чаще всего строят гистограмму именно относительных частот. А вместе с ней нередко и полигон таковых частот.  Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки  , где   – середины интервалов:



41 Аналогом какой теоретической функции является эмпирическая функция распределения.

Эмпирическая функция распределения является аналогом функции распределения непрерывной случайной величинs и приближает теоретическую функцию , которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.
42 Числовые характеристики статистических распределений.






43 Аналогом какой теоретической функции является гистограмма?

Другой характеристикой распределения является таблица (для дискретных распределений) или плотность (для абсолютно непрерывных). Эмпирическим, или выборочным аналогом таблицы или плотности является так называемая гистограмма.
44. Что такое первичные статистические данные?

Это рандомные числа или ответ ниже


45 В чем заключается выборочный метод?

Выборочный метод – статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов. Совокупность исследуемых объектов, интересующих исследователя, называет генеральной совокупностью.
46. Что такое репрезентативная выборка?

репрезентативная выборка — это такая выборка, в которой представлены все подгруппы, важные для исследования. Помимо этого, характер распределения рассматриваемых параметров в выборке должен быть таким же, как в генеральной совокупности
47. Как вы понимаете термин рандомизация?

Способ случайного распределения объектов исследования в основную и контрольную группы с использованием специальных средств
48. Дайте определение эмпирической функции распределения.

Выборочная (эмпири́ческая) фу́нкция распределе́ния в математической статистике — это приближение теоретической функции распределения, построенное с помощью выборки из него.
49. Дайте определение интервального вариационного ряда.

Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
50. Объясните порядок построения гистограммы.

Cтроится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. 

51 Дайте определение свойствам несмещенности, состоятельности и эффективности оценки.

Рассмотрим оценку θ_n числового параметра θ, определенную при n = 1, 2, … Оценка θ_n называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра θ при безграничном возрастании объема выборки

Второе важное свойство оценок – несмещенность. Несмещенная оценка θ_n – это оценка параметра θ, математическое ожидание которой равно значению оцениваемого параметра: М(θ_n) = θ.

С дисперсией оценки связано третье важное свойство метода оценивания – эффективность. Эффективная оценка – это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра.
52. Какими свойствами обладает выборочное среднее?


53. Какими свойствами обладает выборочная дисперсия при известном математическом ожидании?






54. Какими свойствами обладает выборочная дисперсия при неизвестном математическом ожидании?


55 Приведите формулы несмещенной оценки среднего.
56. Приведите формулы несмещенной оценки выборочной дисперсии при известном математическом ожидании и неизвестном математическом ожидании.
57. Дайте определение числа степеней свободы.
58. Дайте определение статистической гипотезы. Что такое нулевая и альтернативная гипотеза?
59. Ошибки 1-го и 2-го рода при формировании статистических гипотез
60. Как определяются область принятия гипотезы и критическая область?
61 Проверка статистических гипотез о параметрах генеральной совокупности.
62 Перечислите этапы построения критерия значимости.
63. Что такое уровень значимости?

Уровнем значимости называется вероятность ошибочного отклонения нулевой гипотезы. Или, иными словами, уровень значимости —это вероятность ошибки первого рода при принятии решения. Для обозначения этой вероятности, как правило, употребляют либо греческую букву α, либо латинскую букву р. В дальнейшем мы будем употреблять букву р.

Говоря о статистической значимости, стоит иметь в виду:

• 
  уровень значимости дает понять, что связь между переменными не случайна;
  
• 
  уровень значимости в статистике может служить доказательством правдоподобности нулевой гипотезы;
  
• 
  в ходе проверки получаем информацию о том, что результат эксперимента является или не является статистически значимым.
  

64 Приведите формулы равномерного, нормального и показательного плотностей распределений вероятностей. Какую роль играет нормальное распределение при решении практических инженерных задач?

Фикция плотности



Функция Лапласа

65. 
    Приведите названия и назначение выборочных распределений.
    

Выборочным распределением называется распределение дискретной случайной величины, принимающей значения х1, х2, …, их с вероятностями 1/n. Соответствующая функция распределения F*(x) называется выборочной или эмпирической функцией распределения и определяется по значениям накопленных частот. 

65. 
    Дайте определение критерия согласия.
    

Критерий согласия — это критерий проверки гипотезы о соответствии эмпирического распределения вероятностей теоретическому.

65. 
    Поясните формулу критерия Пирсона.
    

Формула Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).



n’-теоретические частоты

n_o-эмпирические частоты

65. 
    Объясните процедуру проверки гипотезы о законе распределения генеральной совокупности.
    

Выборочные ряды группируются в дискретный или вариационный ряд с x и соответствующими частотами n



Такой ряд называют эмпирическим рядом

Затем находятся выборочная средняя, выборочная дисперсия и т.д.

Далее рассчитывают теоретические частоты по формуле:




, где

f(z)-функция Гаусса





Xв-сред выборочное значение


Далее вычисляется критерии согласия, которые придумал Карл Пирсон

K =m-r

R-количество оцениваемых интервалов (обычно берется 2)

M-количество интервалов

Критическое значение x²_кр=(α, k)

Если x²_набл<x²_кр,то на уровне значимости 0,05 нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности.

Если x²_набл<x²_кр,то нулевую гипотезу отвергаем, т.е. эмпирические и теоретические частоты значимо, и это различие вряд ли случайно

65. 
    Как находится критическое значение критерия Пирсона?
    

Критическое значение x²_кр=(α, k)

K=m-r

R-количество оцениваемых интервалов (обычно берется 2)

M-количество интервалов

α-проверяется по таблице

65. 
    Какие признаки выборки анализируются для выдвижения гипотезы о законе распределения генеральной совокупности?
    

Если x²_набл<x²_кр,то на уровне значимости 0,05 нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности.

Если x²_набл <x²_кр,то нулевую гипотезу отвергаем, т.е. эмпирические и теоретические частоты значимо, и это различие вряд ли случайно

65. 
    Дайте определение аппроксимации функции. Как находится система нормальных уравнений для определения параметров аппроксимирующей функции?
    

Аппроксимацией (приближением) функции   называется нахождение такой функции   (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций   и   могут быть различные.

Основная задача аппроксимации — построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции

Для решения системы нормальных уравнений был выбран метод Гаусса.

a₁₁ x₁ + a₁₂ x₂ +…+ a_1n X = b₁

a₂₁ x₁ + a₂₂ x₂ +…+ a_2n X = b₂

Составляется с помощью метода наименьших квадратов



Примеры:

https://libraryno.ru/3-3-approksimaciya-funkcii-matmodosipkina/

72 Какие процедуры MatLab используются для решения обыкновенных дифференциальных уравнений?

Функция ode45, методом Рунге-Кутта
Задачи на следующие темы:
- Записатьсистему линейных дифференциальных уравнений в матричном виде

- Указать вектор неизвестных функций заданной системы линейных дифференциальных уравнений,

- Определение оригинала функции по заданному выражению изображения

- Определение выражения для изображения заданной функции (используя определение преобразования Лапласа)

- Напишите алгебраическую систему, которая подучается в результате преобразования по Лапласу заданной системы дифференциальных уравнений

- Элементарные и не элементарные события

• 
  В урне находится разное количество шаров разного цвета. Наугад извлекается 1 шар,. Найти вероятность того, что этот будет указанного цвета.
  

- Набирая номер телефона, абонент забыл определенные цифры, но знает дополнительную информацию о некоторых цифрах. Найти вероятность того, что он наберёт правильный номер.

- Составление закона распределения случайной величины

- Непрерывная случайная величина Х задана функцией распределения F(x).. Найти её плотность распределения f(x).

• 
  Непрерывная случайная величина Х задана функцией распределения F(x), Найти математическое ожидание случайной величины Х
  

- Непрерывная случайная величина Х задана функцией распределения F(x), Найти дисперсию и среднее квадратическое отклонение случайной величины Х

- Непрерывная случайная величина Х задана функцией распределения F(x), Найти вероятность попадания Х в интервал (a; b)

Задачи на использование теорем сложения и умножения вероятностей.

И другие простые задачи на использование классической формулы определения вероятностей.

Задачи на определение вероятностей выпавших очков на подброшенных кубиках, выпавшей стороны подброшенных монет, противоположные события….