ОТНННННН. В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи
 Скачать 2.78 Mb. Скачать 2.78 Mb.
|
Таблица 1.2
Таблица 1.3
Параметр потока отказов и частота отказов для ординарных потоков с ограниченным последствием и при мгновенном восстановлении связаны между собой интегральным уравнением Вольтера второго рода 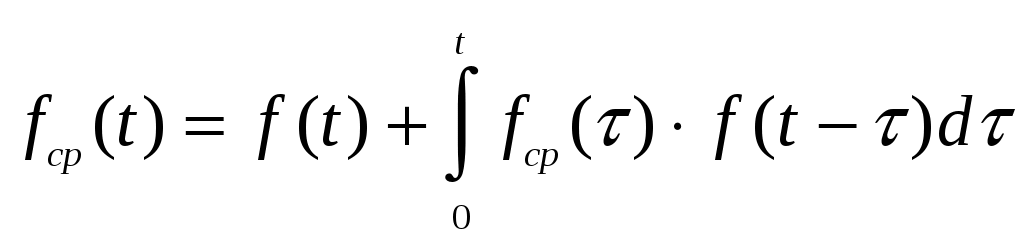 (1.17) (1.17)Как правило, уравнение (1.17) решается в операторной форме 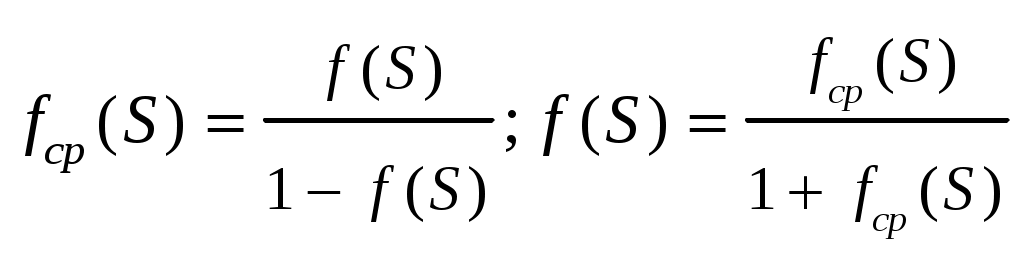 (1.18) (1.18)где 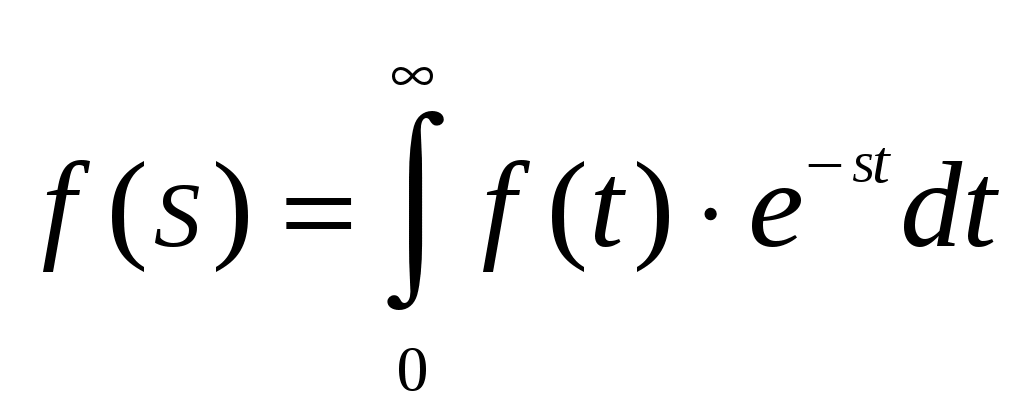 - изображение частоты отказов по Лапласу. - изображение частоты отказов по Лапласу.Представленные соотношения (1.18) позволяют найти одну характеристику через другую, если существуют прямое преобразование функций Наработкой на отказ называется среднее значение времени между соседними отказами. Оценочное значение этой характеристики определяется по статистическим данным об отказах по выражению 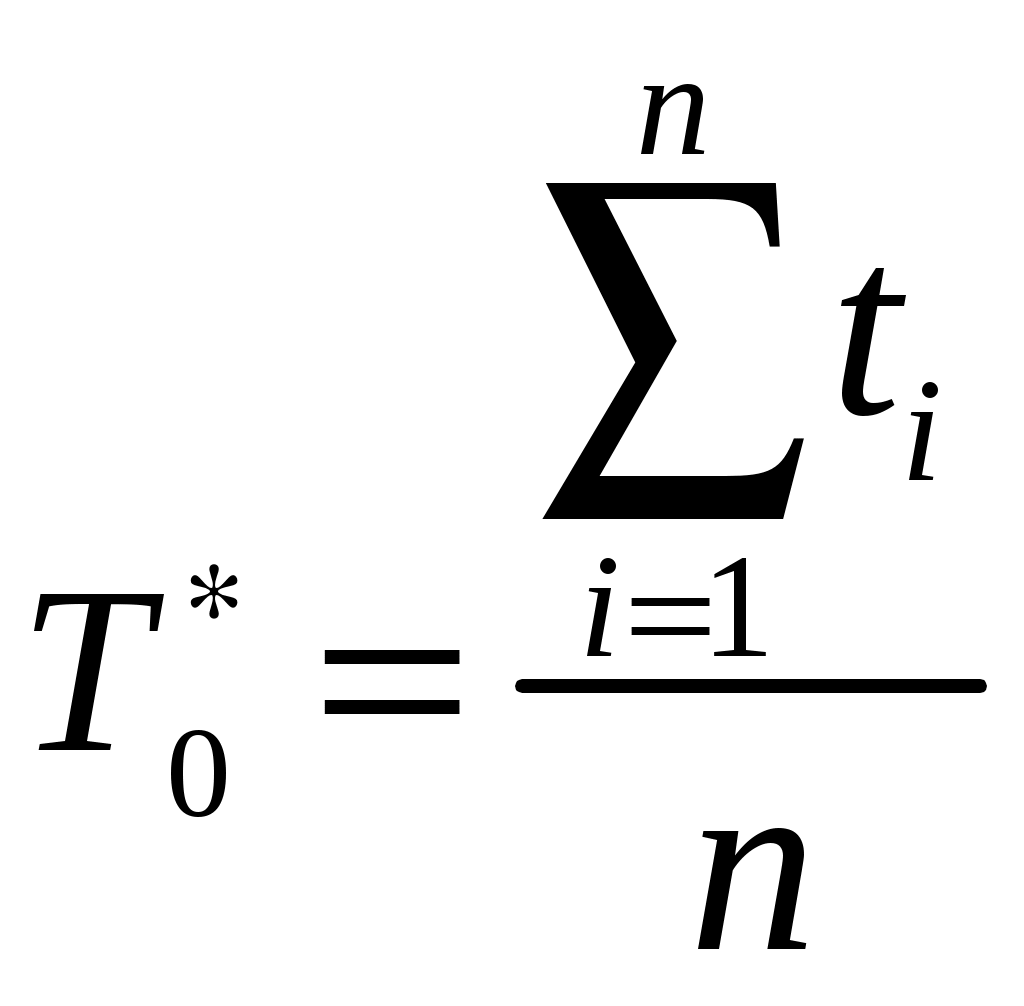 , (1.19) , (1.19)где В том случае, если на испытания поставлено N0образцов, то 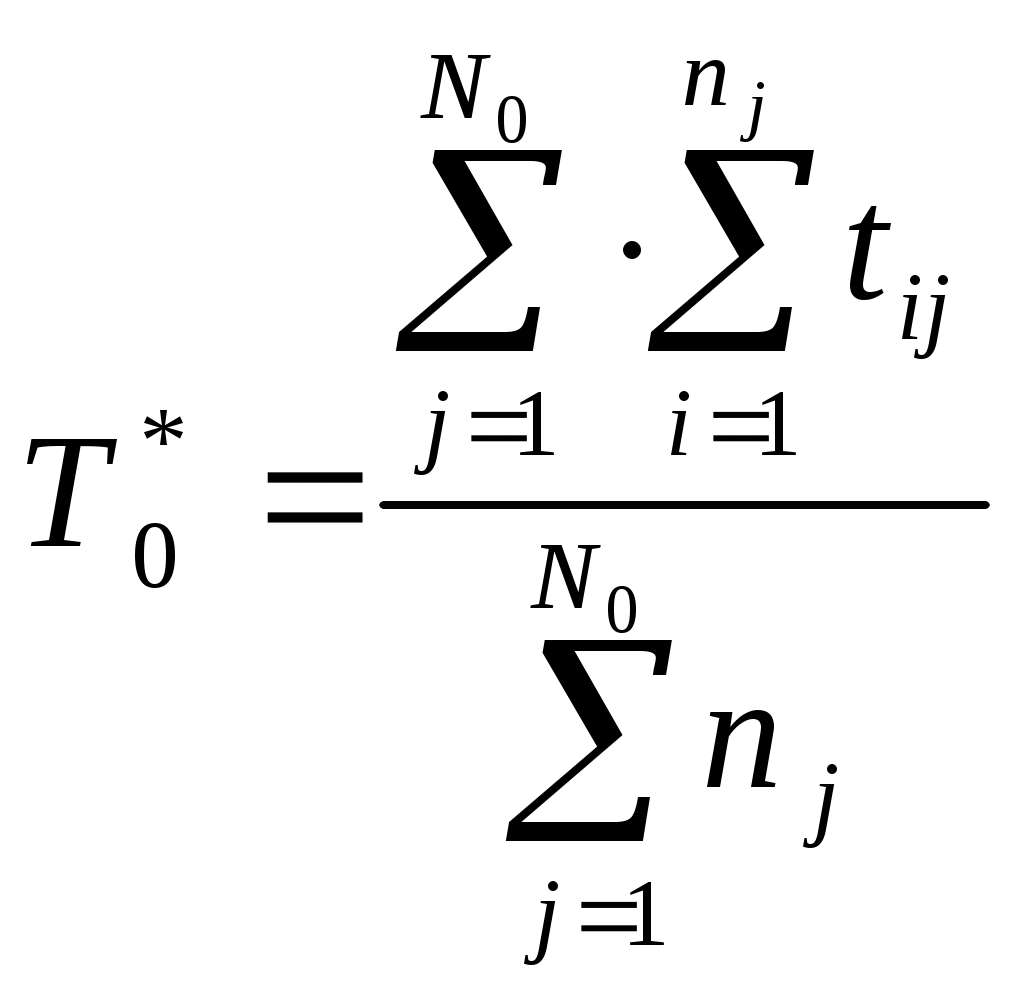 (1.20) (1.20)где Под коэффициентом использования понимается отношение суммарного времени исправной работы к суммарному времени исправной работы и простоев за один и тот же календарный срок. Этот коэффициент обозначается Согласно данному определению 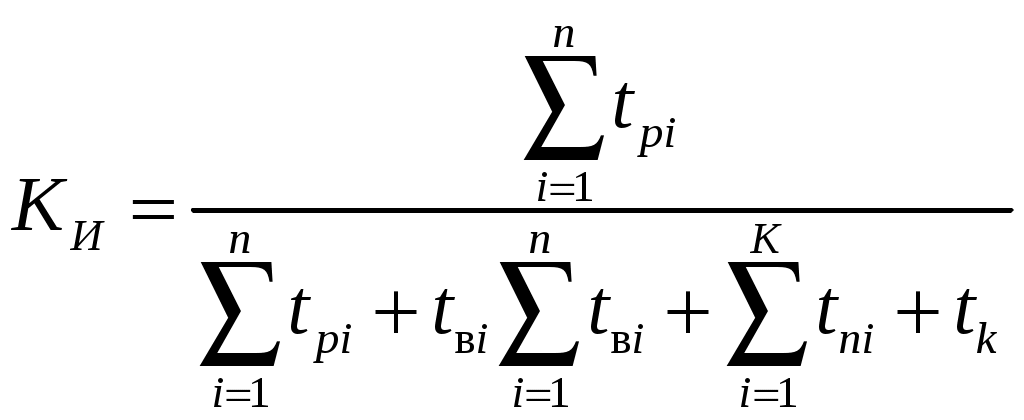 , (1,21) , (1,21)где причине отказов и проведения профилактик; n – число остановок за определенный календарный срок, для которого определяется коэффициент использования; Коэффициентом готовности называется отношение суммарного времени исправной работы к суммарному времени исправной работы и восстановлений, взятых за один и тот же календарный срок 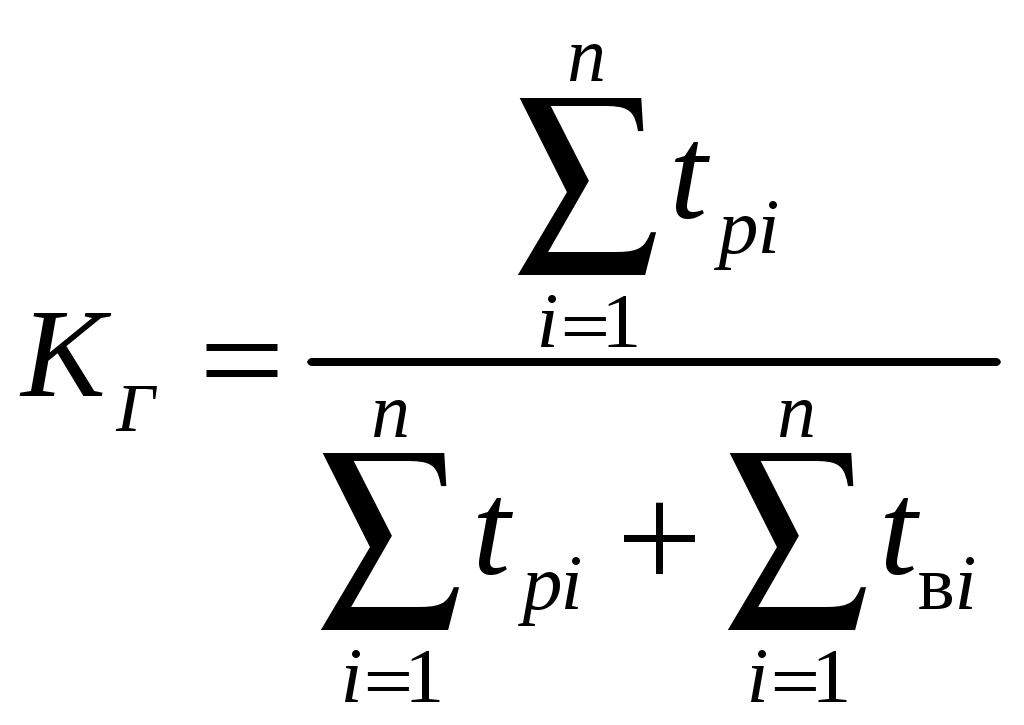 , (1.22) , (1.22)где n – число отказов изделия. В том случае, если поток отказов простейший, то КГ обычно вычисляют по формуле 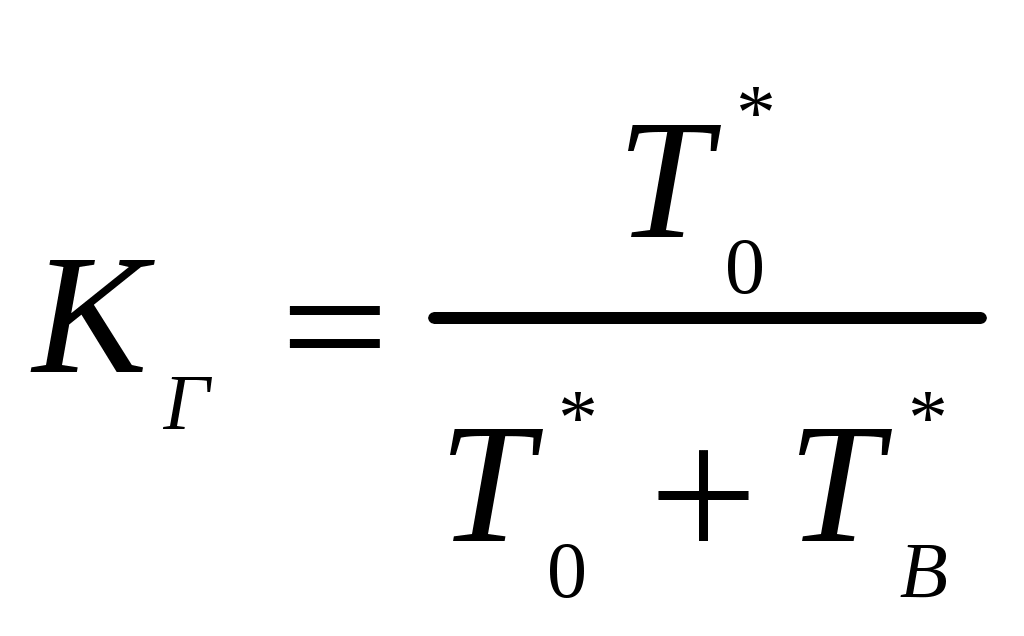 , (1.23) , (1.23)где Выражение (1.23) является статистическим определением коэффициента готовности. Для перехода к вероятностной трактовке величины 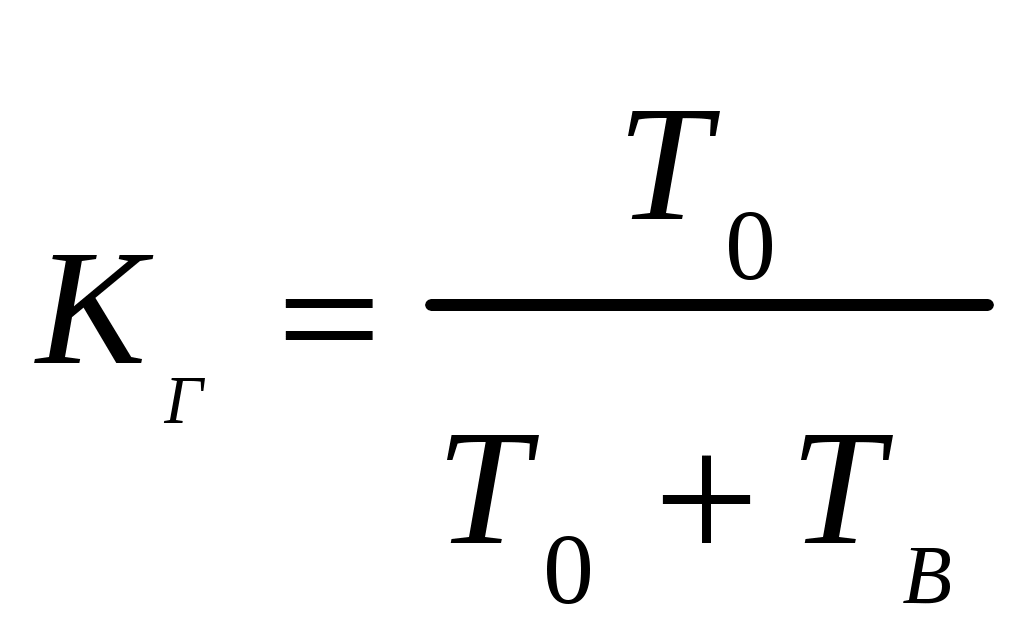 , (1.24) , (1.24)где Коэффициентом простоя называется отношение времени вынужденных простоев к сумме времени исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок. Согласно определению 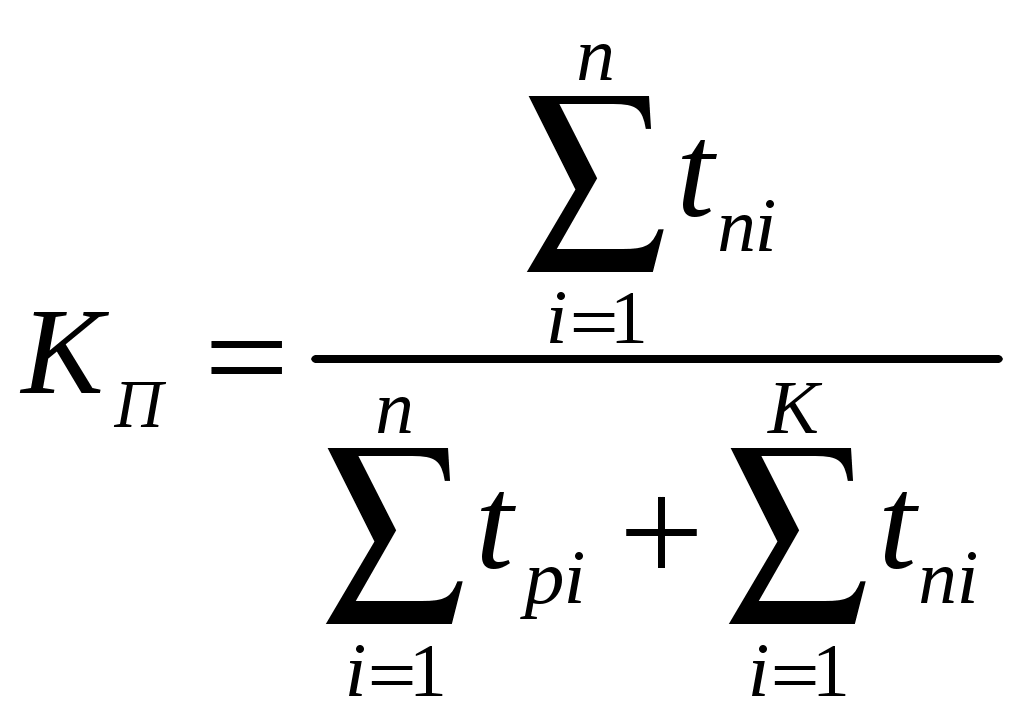 . (1.25) . (1.25)Как следует из определений коэффициента простоя Среднее время восстановления представляет собой математическое ожидание времени восстановления и определяется следующим выражением Статистическая оценка среднего времени восстановления определяется выражением 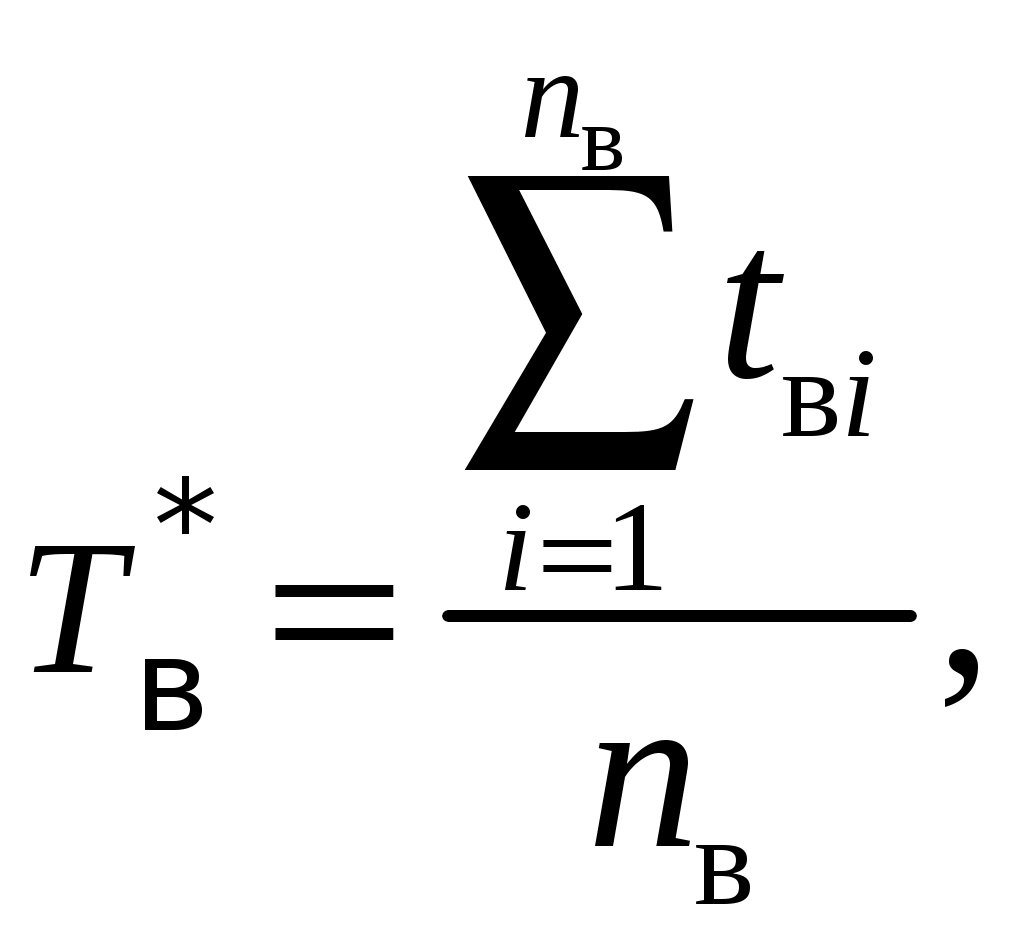 (1.28) (1.28)где В том случае, если известно распределение отказов отдельных элементов системы и время, затраченное на их устранение (время восстановления), то оценку среднего времени восстановления можно определить из выражения 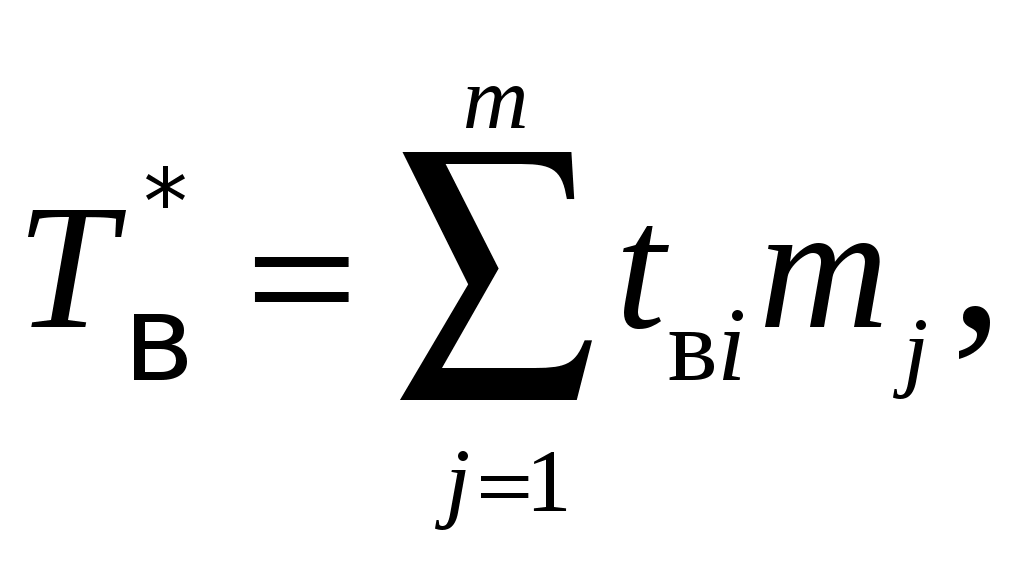 (1.29) (1.29)где 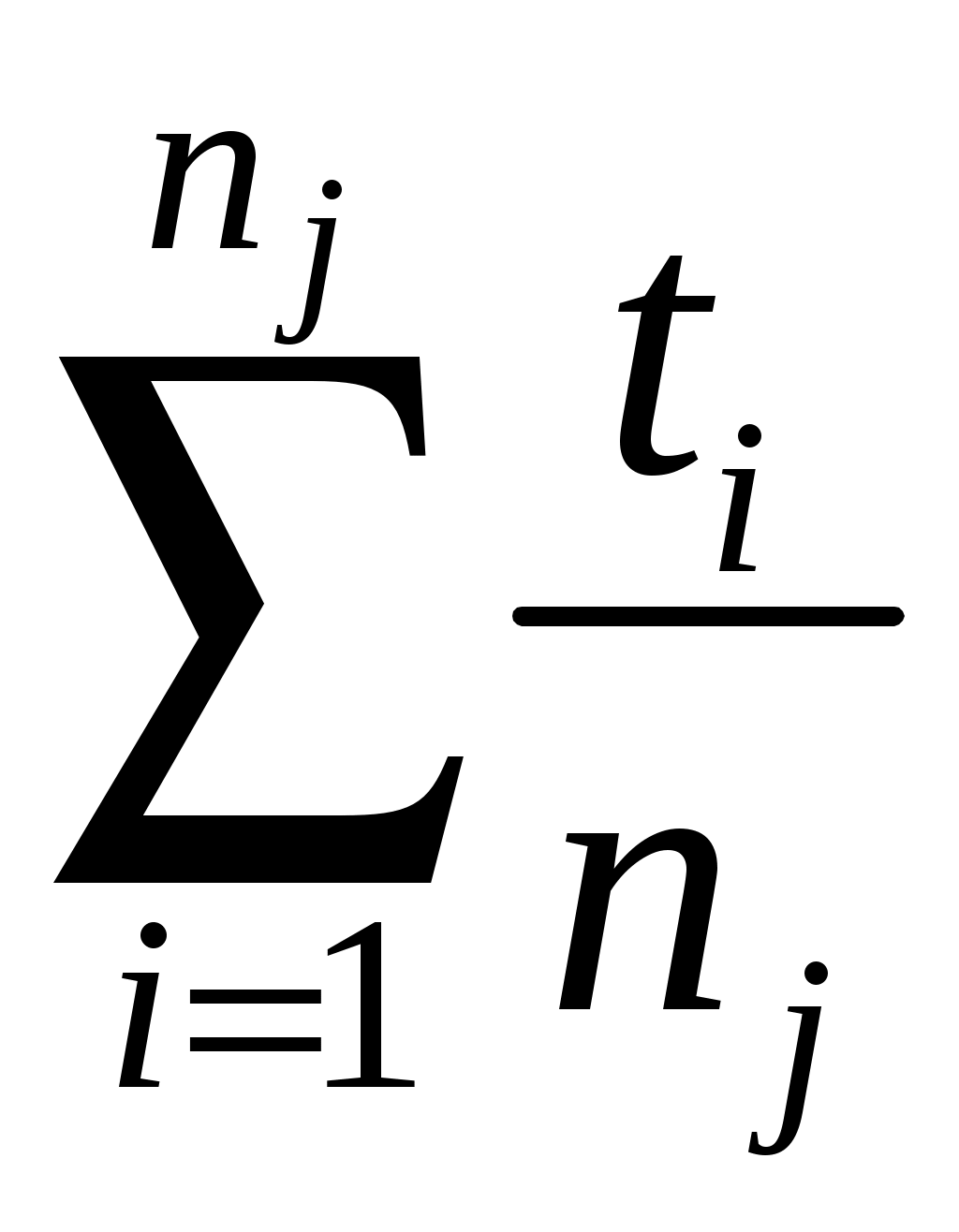 – среднее время восстановления – среднее время восстановления Необходимо помнить, что вероятность отказа в начале эксплуатации мала, а с течением времени эксплуатации эта вероятность возрастает. Это означает то, что вероятность застать систему в исправном состоянии в начале эксплуатации будет выше, чем по истечении некоторого времени. Выражение, которое устанавливает зависимость между коэффициентом готовности и вероятностью застать систему в исправном состоянии в любой момент времени 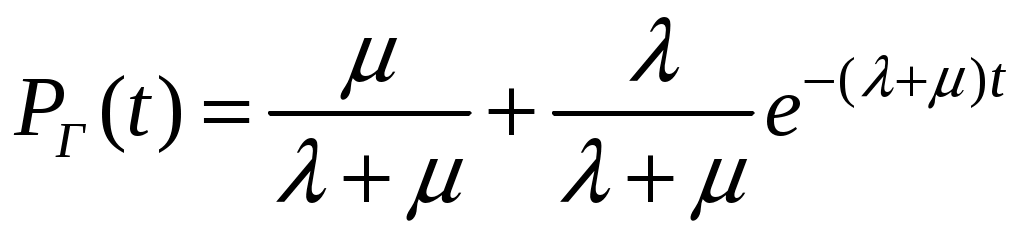 где 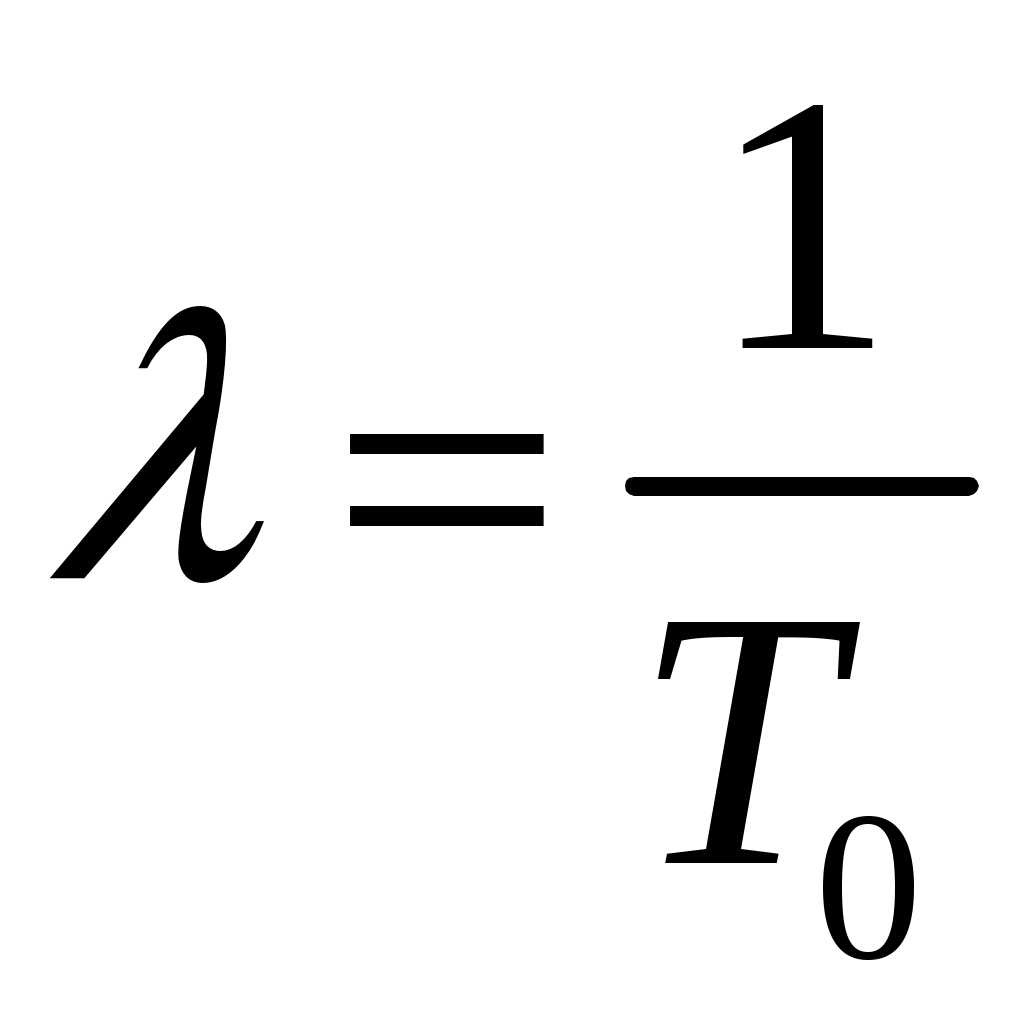 - интенсивность отказов системы; - интенсивность отказов системы;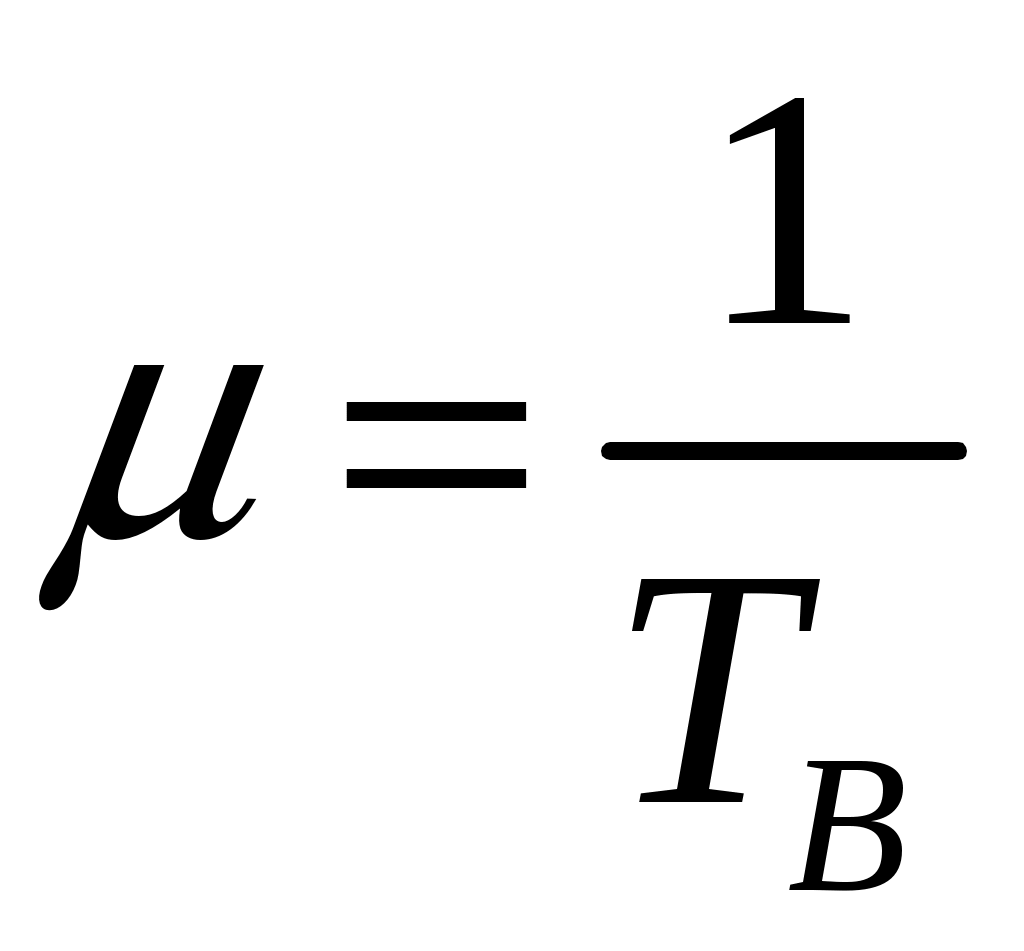 - интенсивность восстановления системы; - интенсивность восстановления системы;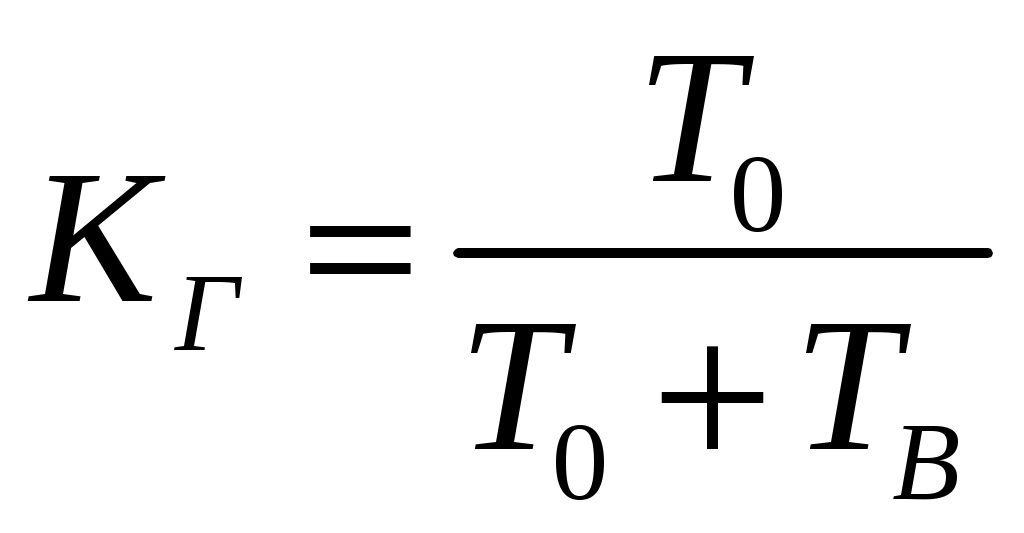 - коэффициент готовности системы - коэффициент готовности системы1.4 Индивидуальные задания по теме «Определение критериев восстанавливаемых систем» Задача 1.3.1 При эксплуатации системы автоматики было зафик-сировано n = 25 + j + 2k отказов ( j – номер варианта, задаётся препо-давателем, k – номер группы ) в течение ( 600 + j + 2k ) ч. При этом распределение отказов по элементам и время затраченное на их устранение ( время восстановления ), приведены в таблице 1.4. Время, затраченное на проследование к месту отказа и профилактику, в среднем больше времени восстановления в 1,6 раза. Требуется определить: среднее время восстановления t*вс ; среднюю наработку на отказ – Т0; коэффициент готовности ( k г ), использования (k и ), простоя (k п ). Задача 1.3.2 В результате эксплуатации N = 1600 восстанавливаемых изделий получены следующие статистические данные об отказах, представленные в таблице 1.5. Число отказовn(t i) фиксировалось через t i часов. При этом к числу отказовn(t i) прибавляется номер варианта j (номер варианта задается преподавателем). Необходимо определить: среднюю наработку до первого отказа изделия Т ср ; вероятность безотказной работы Р( t ); среднюю частоту отказов (параметр потока отказов) f ср( t) ; частоту отказов f( t ); интенсивность отказов ( t ). Пример решение задачи данного типа смотри в /2,4/. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||