ОТНННННН. В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи
 Скачать 2.78 Mb.
|
|
4.2 Примеры решения типовых задач Пример 4.2.1. План испытаний [ n, Б, t0 ]. При испытании  устройств в течении, t0 =500 час. зарегистрировано d=6 отказов устройств. Отказавшие устройства проработали до выхода из строя соответственно 50, 150, 200, 300, 350, 450 часов. Необходимо определить оценку  и двусторонний доверительный интервал для  при  Решение. 1 Определяем суммарную наработку по формуле из табл. 3.1 /2/ 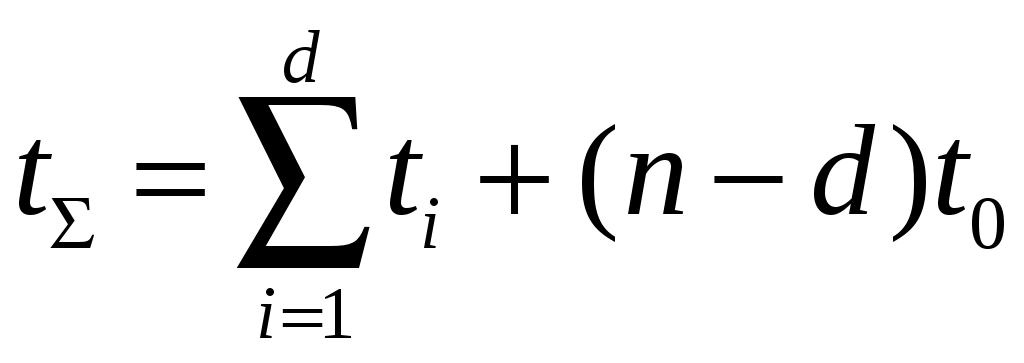 = 50+150 +200 +300 + 350 + 450 + (50 – 6)500 == 1500 + 22000 = 23500 час. 2. Определяем статистическую оценку 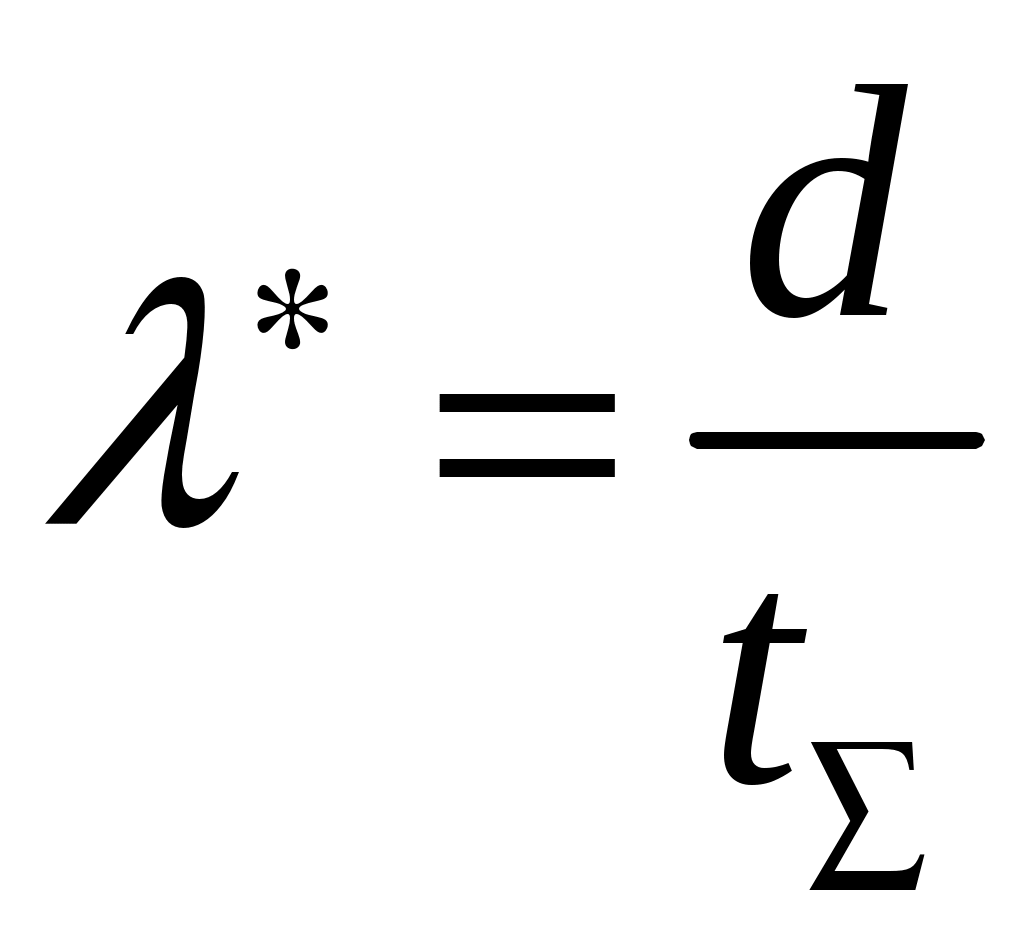формуле из табл. 3.1 /2/ =  = 3. Определяем верхнюю границу. Для определения 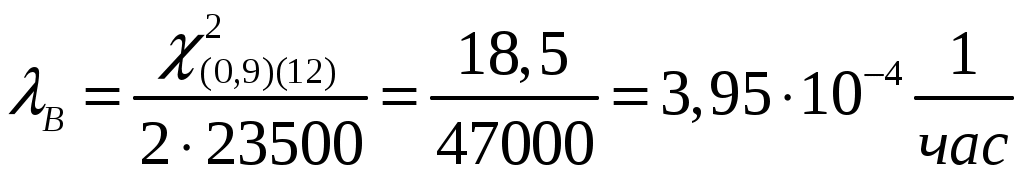 воспользуемся формулой из табл. 3.1 /2/, значения квантилей взять из табл. П.В.1 .4. Определяем нижнюю границу. Для определения 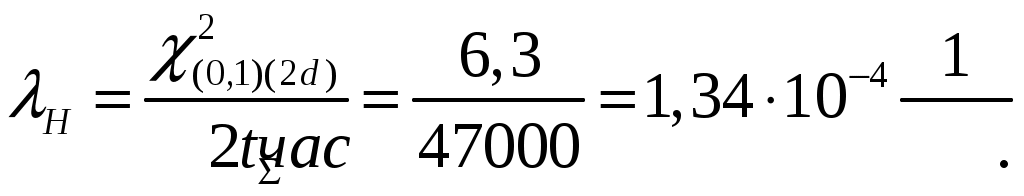 воспользуемся формулой из табл. 3.1 /2/ .Пример 4.2.2. Испытания 100 ламп накаливания, срок службы которых подчиняется нормальному закону, продолжались в течении  За время испытаний отказало 5 ламп с наработкой до отказа в часах соответственно  =50,  = 150,  = 250,  = 300,  = 450. Требуется определить среднюю наработку до отказа ламп и среднее квадратическое отклонение.Решение. 1.Определяем квантили нормального распределения  (см. табл. П.Б.1) для вероятностей    ,  , соответственно, которые равны:  ;  ;  ,  ,  .2. Составляем систему уравнений:      Полученную систему уравнений решаем по методу наименьших квадратов, для чего умножаем левую и правую части каждого уравнения соответственно на  , ,  ,  ,  и затем все уравнения сложим, в результате получим первое, так называемое нормальное уравнение, которое имеет следующий вид  Второе нормальное уравнение получают суммированием уравнений исходной системы, которое имеет следующий вид  Решая полученные нормальные уравнения, получим  час.,  =566,2 час.Для оценки точности полученных значений 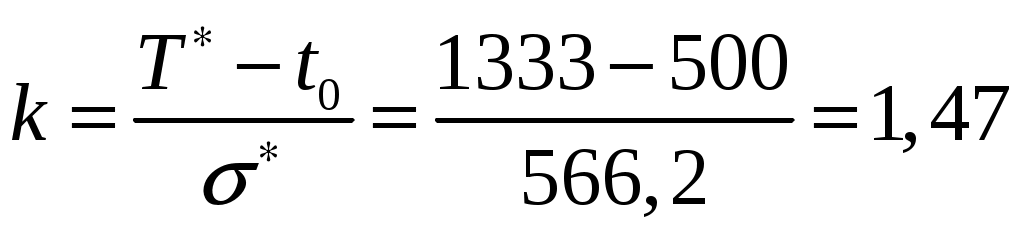 и  определяем .Затем по табл. П.7.7 /4/ находим  .Тогда 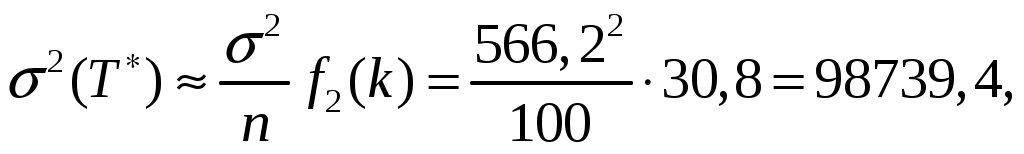 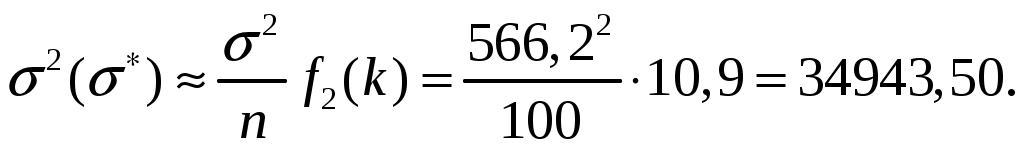 Вычисляя, получим  = 314,2 час.,  = 186,9 час.Как следует из полученных значений, точность определения параметров распределения в условиях данного примера невысокая. Доверительные интервалы величиной  , что соответствует вероятности 95%, в нашем случае составляют  час. час.Пример 4.2.3 Партия изделий, надежность которой нужно проконтролировать, состоит из N=50 экземпляров. Партия считается хорошей, если в ней содержится не более 10% дефектных изделий, и плохой – при содержании 20% дефектных изделий. Риск поставщика и риск заказчика приняты равными и составляют α = β = 0,10. Определить приемное (А0) и браковочное (А1) числа дефектных изделий в выборке объемом n = 20 экземпляров. Решение. Так как партия малая  , а объем выборки относительно велик, то контроль необходимо осуществлять, исходя из гипергеометрического распределения.1 Число дефектных изделий при 10% дефектных изделий в партии составляет D0 =Nq0 = 50×0,10 = 5; при 20% дефектных изделий D1 = Nq1 = 50×0,20 = 10. 2 Для определения приемочного числа дефектных изделий воспользуемся формулой 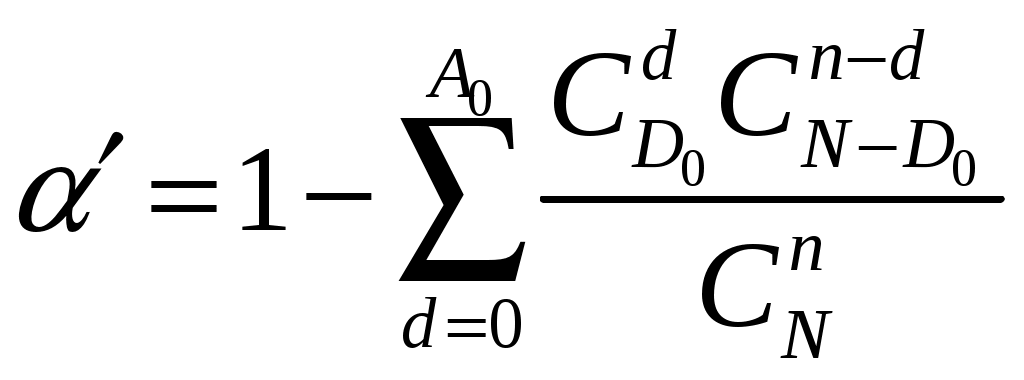 , суммирование вероятностей гипергеометрического распределения производим до тех пор, пока накопленная вероятность не приблизиться к 1-α, т.е. Таким образом, 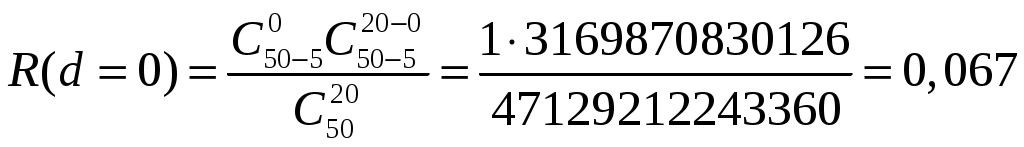 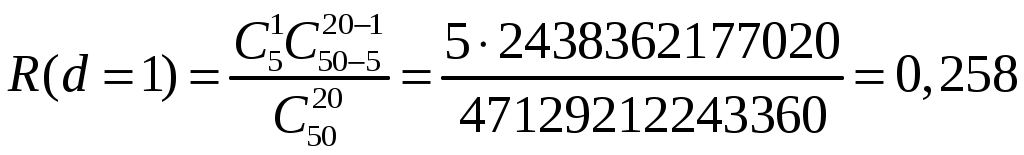 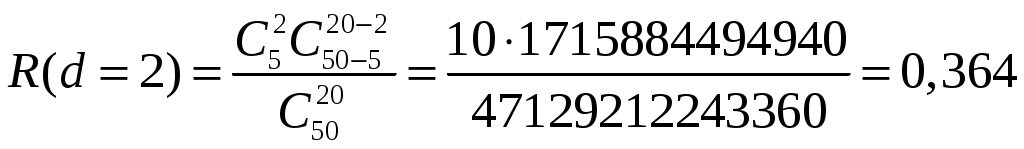 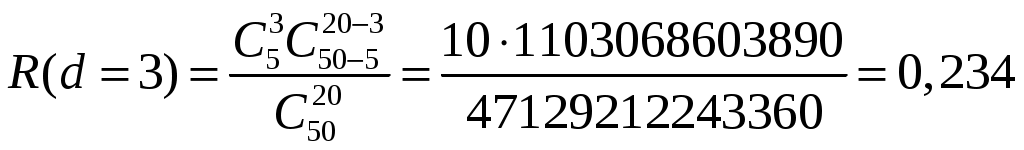  Полученная величина близка к 1-α = 0,90, т.е. фактически риск поставщика близок к принятому :  .Поэтому приемочное число можно взять равным трем (A0=3). Если принять A0=2, то риск поставщика стал бы неприемлемо велик  .3 Аналогичным образом может быть рассчитано браковочное число A1. Для этого по формуле 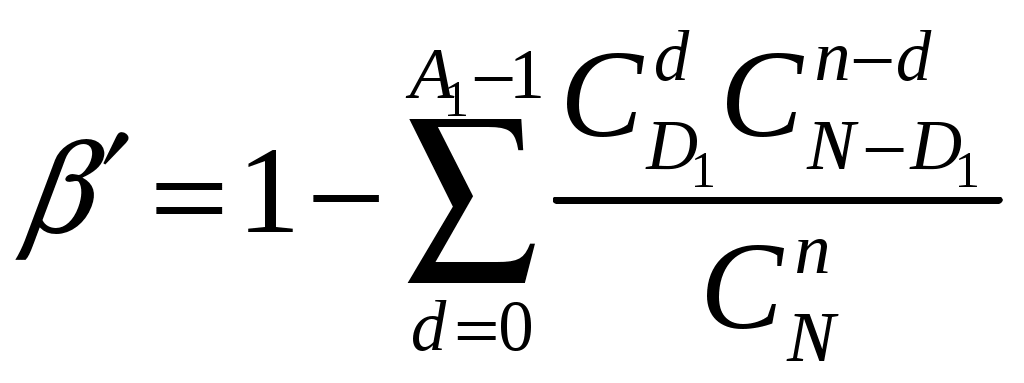 накапливаем вероятности R до тех пор, пока выполняется условие 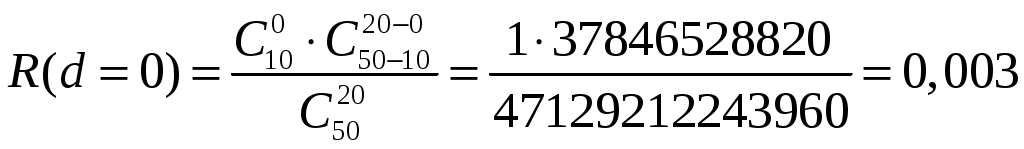 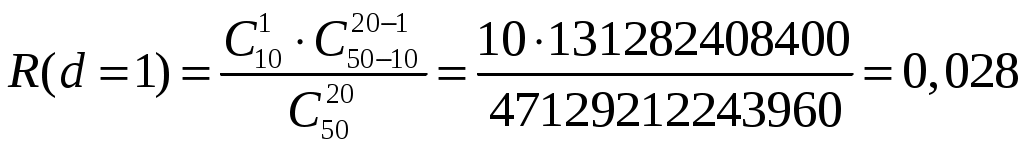 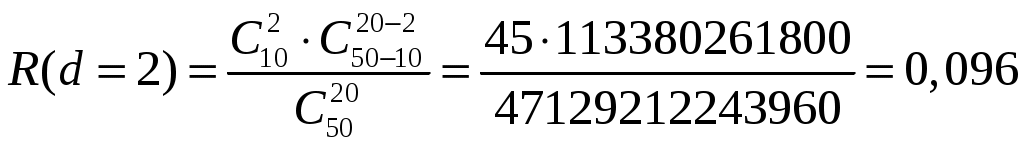   Следовательно, с риском  , близким к первоначально установленному (β = 0,10), при d1= 2 дефектным изделиям в выборке партию можно принять, а при d1 = 3 дефектным изделиям нужно браковать.Приемочное и браковочное A0 = A1 = 3. Это значит, что одиночный контроль не может производиться одновременно в интересах поставщика и заказчика. Пример 4.2.4 Контролю надежности подлежит партия из N = 200 устройств. Необходимо определить приемочное (А0) и браковочное (А1) числа дефектных изделий в выборке из n = 40 изделий. Партия считается хорошей, если в ней содержится 5%, и плохой – если 10% дефектных устройств. Риск поставщика принят равным 0,20, а риск заказчика – 0,10. Решение. Учитывая относительно большой объем контролируемой партии и небольшие значения доли дефектных изделий, целесообразно производить решение, исходя из f-биноминального распределения, в соответствии с формулами 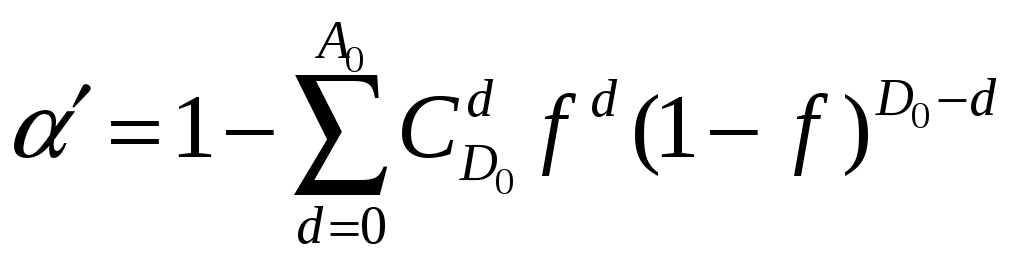 ,  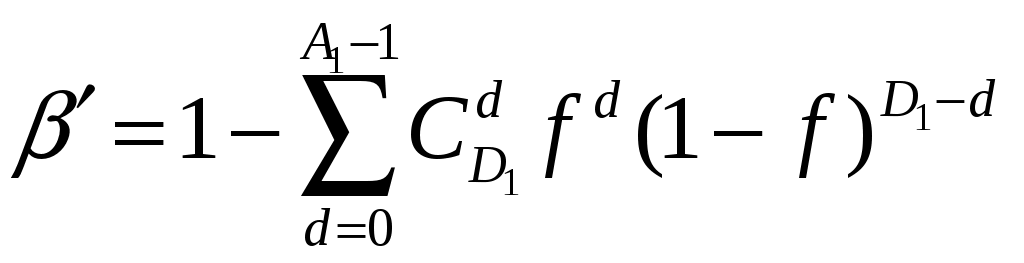1. Рассчитываем величины f, D0 и D1:  D0=Nq0=10;  .2. Приемочное число А0 определяется суммированием вероятностей f-биноминального распределения до величины  близкой к  : Далее вычисляем вероятности R(d) и суммируем их:       Следовательно, можно принять приемочное число равным A0 = 2 с риском поставщика  или равным A0 = 3 с риском поставщика  .В том случае, если требуется фактический риск приблизить к заданному, то это можно сделать при постоянном объеме партии и доле дефектных устройств, варьируя объемами выборки и приемочными числами. 3. Браковочное число A1 определяется аналогично приемочному числу с той лишь разницей, что в данном случае нужно руководствоваться формулой для определения  (приведена выше в задаче) и суммировать вероятности f–биноминального распределения до величины  Определяем вероятности f–биноминального распределения  ,  Так как R( d ≤ 1 ) = 0,010 + 0,058 = 0,068 R( d ≤ 2 ) = 0,010 + 0,058 + 0,137 = 0,205, то, очевидно, целесообразно считать браковочным числом A1 = 2, тогда риск заказчика будет более близким к установленному. Пример 4.2.5. Последовательному контролю надежности подлежит партия, состоящая из N = 100 невосстанавливаемых изделий. Партия считается хорошей при доле дефектных изделий q0 = 0,05 и плохой – при q1 = 0,10. Риск поставщика равен риску заказчика и составляет 0,1. Требуется определить приемочные (mпр) и браковочные (mбр) числа испытаний при числе дефектных изделий dm = 0, 1, 2, 3, 4 и 5, а также построить график контроля по характеристическим точкам и принять решение в случае появления четырех отказов при 25 испытаниях. Решение. Так как общий объем исследуемой совокупности мал, необходимо осуществлять контроль по f-биноминальному плану. Для того, чтобы определить приемочные и браковочные числа и построить график контроля необходимо произвести следующие вычисления. 1. Определяем число дефектных изделий в партии при нулевой и альтернативной гипотезах:  ;  2. Находим значения оценочных нормативов А и В: 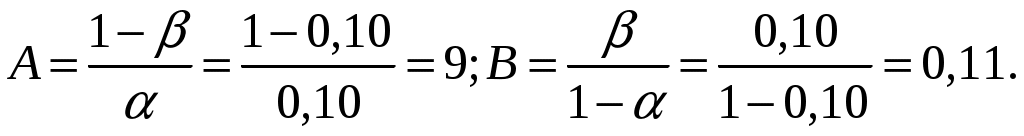 3. Для определения характеристических точек графика плана подсчитываем значения c и r:    4. Определяются приемочные числа по выражению  , в которое подставляем постоянные величины N, B, c, r и вычисляем переменную для каждого числа дефектных изделий величину.Следовательно,  ;  ; , ;  ; и т. д. Для подсчета браковочных чисел используется выражение   . Очевидно, что эта формула имеет смысл при  , что в соответствии с таблицей биноминальных коэффициентов имеет место при dm ≥ 3. Для d = 3  ;  и т. д.После расчета всех приемочных и браковочных чисел результаты представлены в таблице 4.2.1 Таблица 4.2.1
5. Определяются характеристические точки для построения графика плана: а) dm = 0,  ; б) dm = D0 = 5,   ;в) dm =  ; m = N= 100Для построения графика плана строим прямоугольные оси координат с ординатами dm = 0, 1, 2, …., 10 и абсциссами m = 1,2, 3, …, 100 и отмечаем точки а ,б и в. Далее точку в соединяем с точками а и б. 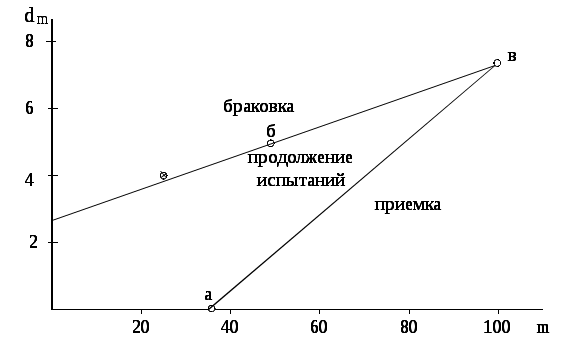 Рисунок 4.1. График контроля Заданная по условию примера рабочая точка d = 4, m = 25 попадает в область браковки (смотри график контроля рис.4.1). Следовательно, партию можно забраковать и испытания прекратить. Правильность решения можно проверить по правилу браковки:  С этой целью посчитаем  Так как 14,9 > 9, то партия бракуется. |