вычислительные системы в информатике. вычислительные системы (копия). В россии в xvixvii веках появилось намного более передовое изобретение

• Название: В россии в xvixvii веках появилось намного более передовое изобретение
• Анкор: вычислительные системы в информатике
• Дата: 23.05.2023
• Размер: 0.79 Mb.
• Имя файла: вычислительные системы (копия).docx
• Тип: Анализ; #1153303
• страница: 2 из 12

Если из контекста не ясно, к какой системе счисления относится запись, то основание системы записывается после числа в виде нижнего индекса.

На­пример, одно и то же число 137 запишется в двоичной, восьмеричной и шестнадцатеричной системе следующим образом:  137₁₀  =  10001001₂ =  211₈ = 89₁₆.

Арифметические действия с числами в восьмеричной и шестнадцатеричной системах счисления выполняются по аналогии с двоичной и десятичной системами.

Для этого необходимо воспользоваться соответствующими таб­лицами (например, табл. 1.2).

Таблица 1.2. Арифметические действия в восьмеричной системе счисления

 

	Сложение									Умножение
	+	0	1	2	3	4	5	6	7	X	0	1	2	3	4	5	6	7
	0	0	1	2	3	4	5	6	7	0	0	0	0	0	0	0	0	0
	1	1	2	3	4	5	6	7	10	1	0	1	2	3	4	5	6	7
	2	2	3	4	5	6	7	10	11	2	0	2	4	6	10	12	14	16
	3	3	4	5	6	7	10	11	12	3	0	3	6	11	14	17	22	25
	4	4	5	6	7	10	11	12	13.	4	0	4	10	14	20	24	30	34
	5	5	6	7	10	11	12	13	14	5	0	5	12	17	24	31	36	43
	6	6	7	10	11	12	13	14	15	6	0	6	14	22	30	36	44	52
	7	7	10	11	12	13	14	15	16	7	"0	7	16	25	34	43	52	61

 

 

Преобразование чисел из одной системы счисления в другую

Преобразование из десятичной в прочие системы счисления производится в с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.

Рассмотрим алгоритм перевода на примере целого числа 137 в двоичную систему. Разделим его нацело на 2, получим 137:2 = 68, остаток 1. Полученный результат можно записать следующим образом:

             137 =  68 × 2¹ +1 × 2⁰.

Продолжим операцию деления дальше

 68 : 2 = 34,  остаток 0,

137  =  (34×2 + 0)× 2¹+ 1× 2⁰ = 34 × 2² + 0×2¹ + 1× 2⁰;

34 :  2  =  17, остаток 0,

137  =  (17 × 2 + 0)× 2² + 0×2¹ + 1×2⁰  =  17× 2³ + 0× 2² + 0×2¹ + 1×2⁰;

17:2 = 8, остаток 1,

137  =  (8×2 + 1) × 2³ +0×2²+0 × 2¹ + 1×2⁰  = 8×2⁴  + 1× 2³ + 

+ 0× 2² + 0× 2¹+1 × 2⁰;

                      8:2 = 4, остаток 0,

137  =  (4×2 + 0) × 2⁴+1 × 2³ + 0× 2² + 0×2¹ + 1× 2⁰ = 4×2⁵ +

+ 0 × 2⁴+ 1 × 2³+ 0 × 2² + 0 × 2¹ +1 × 2⁰;

                 4:2 = 2, остаток 0,

137  = ( 2 × 2 + 0) × 2⁵+ 0 × 2⁴ +1 × 2³+ 0 × 2²+ 0 × 2¹+ 1 × 2⁰ =

=  2 × 2⁶+ 0 ×2⁵+ 0 ×2⁴+ 1 × 2³ + 0 × 2² + 0 × 2¹ + 1× 2⁰;

                 2:2 = 1, остаток 0,

137  = ( 1 ×2 + 0) ×2⁶ + 0 × 2⁵+ 0 × 2⁴ + 1 × 2³ +  0 × 2²+ 0 × 2¹ +

+  1× 2⁰  = 1 × 2⁷ + 0 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2² + 0 × 2¹+ 1 × 2⁰.

Далее процесс продолжать нельзя, т. к. 0 не делится нацело на 2.

 Таким образом, последовательное деление нацело на 2 позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа:  137₁₀ =10001001₂. 

Читая частное и остатки от деления в порядке, обратном получению, най­дем двоичную запись числа. Для других систем счисления все описанные действия выполняются аналогичным способом.

Например, это же число 137 в восьмеричную и шестнадцатеричную систему счисления переводится по похожим схемам.

Для дробных чисел правило последовательного деления заменяется пра­вилом последовательного умножения.

Переведем 0.2 из десятичной системы счисления   в   двоичную.   Умножим   0.2   на   2,   т.е.    0.2 × 2 = 0.4    или

0.2  = ( 0 + 0.4) × 2^-1  = 0 × 2^-1  + 0.4 × 2^-1 .

0.4 × 2  =  0.8, 0.2  = 0 × 2^-1 + (0 + 0.8) × 2^-1 × 2^-1 = 0 × 2^-1 + 0 × 2^-2 + 0.8 × 2^-2;

0.8 × 2 = 1.6,  

0.2  =  0 × 2^-1 + 0 ×2^-2  + (1 + 0.6 ) × 2^-3 = 0 × 2^-1  + 0 × 2^-2 + 1×2^-3 + 0.6 × 2^-3;

                        0.6 × 2 = 1.2,

  0.2  =  0× 2^-1 + 0 × 2^-2  +1 × 2^-3  + (1 + 0.2) × 2^-4 = 0 × 2^-1 +  0 × 2^-2  + 1 × 2^-3  + 1 × 2^-4  +0.2 × 2^-4 ;

0.2 × 2 = 0.4,  0.2  =  0 × 2^-1 + 0 × 2^-2  + 1 × 2^-3  +  1 × 2^-4  + (0 + 0.4) × 2^-5 = 0 × 2^-1  + 0 × 2^-2 + 1 × 2^-3 +1 × 2^-4 + 0 × 2^-5  + 0.4 × 2^-5 ,

т.е. 02₁₀ =0.00110011...₂. 

 Все вышеприведенные выкладки можно свести в табл. 1.3.

 

		Таблица 1.3.
	0	0.2 2
	0	0.4 2
	1	0.8  2
	1	0.6    2
	0	0.2 2
	……..	……..

Заметим, что в десятичной системе правильная дробь переводится в деся­тичную дробь в конечном виде только тогда, когда ее знаменатель имеет множители только степени двоек и пятерок, т. е. дробь имеет вид  к / (2^т 5^п ).

Аналогично в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки. Таким образом, большинство деся­тичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями.

Обратный перевод чисел из двоичной системы счисления в десятичную производится методом подстановки.

Для этого необходимо представить чис­ло:

137.2₁₀   =  10001001.00110011...₂ , =

=  1 × 2⁷ +1 × 2³ +1 × 2⁰  + 1 × 2^-3  +1 × 2^-4 +1 × 2^-7  +1 × 2^-8  +….. =

 ≈ 137.1992...₁₀.

Между двоичной системой счисления, восьмеричной и шестнадцатеричной существует связь, позволяющая легко переводить числа из одной системы в другую.

 Чтобы перевести число из двоичной системы счисления в восьме­ричную, надо от десятичной запятой вправо и влево выделить группы по три цифры (триады) и каждую группу независимо от других перевести в одну восьмеричную цифру.

 Для перевода в шестнадцатеричную систему необхо­димо выделять по четыре цифры (тетрады) и переводить каждую группу в одну шестнадцатеричную цифру.

 

Представление целых и действительных чисел в двоичном коде

Совокупность двоичных разрядов данных в ЭВМ образуют некий битовый рисунок. Группа из восьми взаимосвязанных битов называется байтом. Байт — это минимальная по размеру адресуемая часть памяти компьютера.

Существует несколько типов чисел.

 Числа могут быть положительные неотрицательные, целые точные, дробные точные, рациональные, иррацио­нальные, дробные приближенные. Оптимального представления в памяти ЭВМ для всех типов чисел создать невозможно, поэтому для каждого в от­дельности типа создается собственный способ представления.

Целые положительные числа от 0 до 255 можно представить непосредст­венно в двоичной системе счисления, при этом они будут занимать один байт в памяти компьютера (табл. 1.4).

Таблица 1.4. Представление целых положительных чисел в двоичной системе счисления

 

	Число	Двоичный код
	0	0000 0000
	1	0000 0001
	2	00000010
	3	0000 0011
	……	………
	255	11111111

 

Знак отрицательного числа кодируется обычно старшим битом, нуль ин­терпретируется как плюс, единица как минус.

Поскольку один бит будет занят, то одним байтом могут быть закодированы целые числа в, интервале от -127 до +127. Такой способ представления целых чисел называется прямым кодом.

Существует способ кодирования отрицательных целых чисел в обратном коде.

В этом случае положительные числа совпадают с положительными числами в прямом коде, а отрицательные получаются в результате вычитания из двоичного числа 1 0000 0000 соответствующего положительного числа, например, число  -7  получит код 1111 1000. Целые числа больших диапазонов представляются в двухбайтовых и четырехбай­товых адресах памяти.

Точность представления действительных чисел в памяти ЭВМ ограниче­на. Для представления действительных чисел используется форма их записи, называемая формой с плавающей точкой:

Х = т – g^p,^:

где:  т— мантисса числа,  g — основание системы счисления, р— целое число, называемое порядком.

При этом для десятичной системы счисления , мантисса выбирается в диапазоне 1 /g ≤ │m │ < g , т. е. 0.1≤│m│ < 1. Такая форма

представления называется нормализованной.

Существует несколько международных стандартов представления дейст­вительных чисел в памяти компьютера. Рассмотрим четырехбайтовый стан­дарт (рис.1.).

Здесь зафиксированы три группы разрядов. Первый разряд хранит знак мантиссы. За ним следуют разряды, определяющие порядок. С первого по двадцать третий разряд располагается сама мантисса числа. Вместо истинного порядка хранится число, называемое характеристикой (или смещенным порядком). Характеристика равна порядку со смещением, причем смещение используется для более удобного хранения положительных и отрицательных действительных чисел.   

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диа­пазон представления чисел в компьютере при заданном формате.

 

 

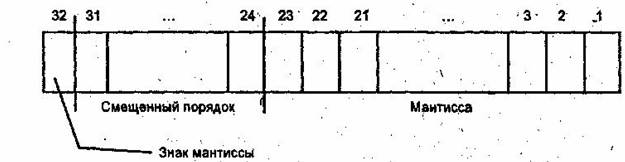
Рис. 1. Четырехбайтовое представление действительного числа

Для представления основных видов информации (числа, символы, графи­ка, звук) в системах программирования используются специального вида аб­стракции — типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных.

Кодирование текстовых и символьных данных

В двоичной системе счисления кодирование "внешних" символов основывается на сопоставлении каждому из них определенной группы двоичных знаков. Двоичное кодирование символьных данных производится заданием кодовых таблиц, в которых каждому символу ставится в соответствие одно- или двухбайтовый код. Восьми двоичных разрядов достаточно для кодирования 256 различных cимволов. Этого количества достаточно, чтобы выразить все символы английского и русского алфавита, а также знаки препинания, символы основных арифметических операций и некоторые специальные символы.

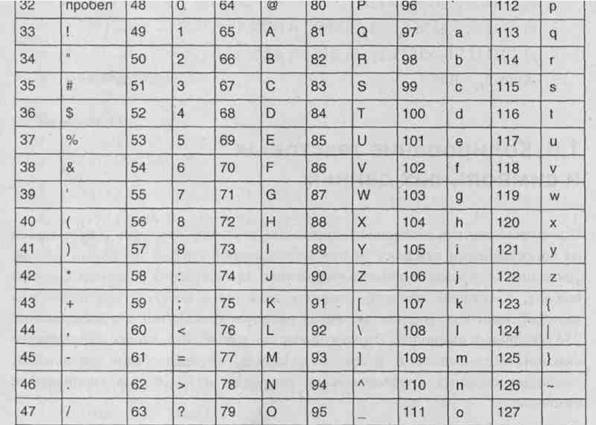
Наиболее популярная таблица АSСІІ (американский стандартный код информационного обмена) разработана институтом стандартизации США) в 1981 году (табл. 1.10).

Коды с 0 до 127 составляют базовую (основную) таблицу, коды со 128 по 255 — расширенную (дополнительную) таблицу. Дополнительная таблица отдана национальным алфавитам и символам псевдографики.

Аналогичные системы кодирования текстовых данных были разработаны и в других странах. Так, в СССР действовала система кодирования КОИ-8 (код информационного обмена восьмизначный). Компанией Microsoft была введена кодировка символов русского языка, известная как кодировка  Windows1251.

Во многих азиатских странах 256 кодов не хватило.

В 1991 году произво­дители программных продуктов (Microsoft , IВМ, Арр1е) выработали единый стандарт Unicode 3.0.

 Этот код построен по 31-битной схеме. Все текстовые документы в этой кодировке вдвое длиннее, зато она содержит буквы латин­ского и многих национальных алфавитов, спецсимволы и т. п.

 

                             Таблица 1.10. Базовая таблица кодировки АSСІІ

 

Кодирование графических данных

Различают три вида компьютерной графики: растровую, векторную и фрак­тальную.

Они отличаются принципами формирования изображения при ото­бражении на экране монитора или при печати на бумаге.

Если графические объекты формируются в виде множества точек (пиксе­лов) разных цветов и разных яркостей, то это называется растровой графи­кой. В Интернете применяются только растровые иллюстрации. Основным элементом растрового изображения является точка. Если изображение экран­ное, то эта точка называется пикселом. В зависимости от того, на какое гра­фическое разрешение экрана настроена операционная система компьютера, на экране могут размещаться изображения 640x480, 800x600, 1024x768 и бо­лее пикселов.

При кодировании растровых изображений в памяти компьюте­ра должна храниться информация о каждом пикселе. С размером изображе­ния непосредственно связано его разрешение. Этот параметр измеряется в dpi      ( точек на дюйм).

В растровой графике общепринятым на сегодняшний день считается пред­ставление черно-белых иллюстраций в виде комбинации точек с 256 града­циями серого цвета. Эти мельчайшие точки образуют характерный узор, называемый растром. Точно так же изображают информацию периферийные устройства печати.

У растровых изображений два основных недостатка.

 Во-первых, очень большие объемы данных. Для активных работ с большими размерными иллюстрациями типа журнальной полосы требуются компьютеры с большими размерами оперативной памяти (128 Мбайт и более).

Во-вторых, растровые изображения невозможно значительно увеличить без серьезных искажений.

Эффект искажения при увеличении точек растра называется пик­селизацией.

В отличие от растровой в векторной графике изображение представляет собой совокупность простых элементов: прямых линий, дуг, окружностей, эллипсов, прямоугольников и т. п., которые называются графическими при­митивами.

Положение и форма графических примитивов задаются в системе графических координат, связанных с экраном. В векторной графике объем памяти, занимаемой, например линией, не зависит от размеров линии, по­скольку линия представляется в виде формулы, а точнее в виде нескольких параметров. Перед выводом на экран каждого объекта программа векторной графики производит вычисление координат экранных точек в изображении объекта. Аналогичные вычисления производятся при выводе объектов на принтер.

Векторная графика лишена недостатков растровой, но в ней сложно соз­давать художественные иллюстрации, поэтому чаще всего ее используют для чертежных и проектно-конструкторских работ.

Фрактальная графика, как и векторная, — вычисляемая, но отличается от нее тем, что никакие объекты в памяти компьютера не хранятся. Изображе­ние строится по уравнениям, поэтому ничего, кроме формулы, хранить не надо. Изменение коэффициентов в уравнении позволяет получить совершен­но другую картину.

Для кодирования цветных графических изображений применяется принцип декомпозиции —  разложение произвольного цвета на основные составляю­щие.

Существует множество различных типов цветовых моделей, но в ком­пьютерной графике, как правило, применяется не более трех. Эти модели из­вестны под названиями: RGB, CMYK,HSB

Цветовая модель RGB. В ней в качестве составляющих используются три цвета: красный (Red), зеленый (Qгееп) и синий (Вluе). Считается, что любой цвет состоит из этих трех компонент. Совмещение всех трех цветов дает ней­тральный цвет (серый), который при большой яркости стремится к белому цвету. Метод получения нового оттенка суммированием яркостей состав­ляющих компонент называется аддитивным. Он применяется всюду, где цвета изображения рассматриваются в проходящем цвете, т. е. на просвет: в мониторах, слайд-проекторах и т. п.

Каждому из основных цветов для кодирования нужно восемь двоичных разрядов, для трех — 24, а 2²⁴  = 16.5 млн. Таким образом, эта система обес­печивает однозначное определение 16.5 млн. цветов, что близко к чувстви­тельности человеческого глаза. Режим представления цветной графики с ис­пользованием 24 двоичных разрядов называется полноцветным (Тruе Со1ог).

Цветовая модельCMYK. Эту модель используют для подготовки не эк­ранных, а печатных изображений. Они отличаются тем, что видят их не в проходящем, а в отраженном цвете. Чем больше краски положено на бума­гу, тем больше света она поглощает и меньше отражает. В отличие от модели RGB, увеличение количества краски приводит не к увеличению визуальной яркости, а к ее уменьшению. Поэтому для подготовки печатных изображений используется не аддитивная модель, а субтрактивная (вычитающая) модель. Цветовыми компонентами этой модели являются не основные цвета, а до­полнительные, т. е. те, которые получаются в результате вычитания основных цветов из белого: голубой (Суаn), пурпурный (Маgenta) и желтый (Yellоu). Так как цветные красители по отражающим свойствам не одинаковы, то для повышения контрастности применяется еще черный (В1аск) цвет.

В типографиях цветные изображения печатаются в несколько приемов. Накладывая на бумагу поочередно голубой, пурпурный, желтый и черный отпечатки, получают полноцветную иллюстрацию.

Цветовая модель НSВ. Если модель RGB наиболее удобна для компьюте­ра, модель  CMYK  —  для типографии, то модель HSB наиболее удобна для

человека. В модели НSВ также три компонента: оттенок цвета (Нuе), насы­щенность (Saturation)  и яркость цвета (Вrightness).

Регулируя эти три компо­ненты, можно получить столь же много произвольных цветов, как и при ра­боте с другими моделями. Эта модель удобна для применения в тех графических редакторах, которые ориентированы не на обработку готовых изображений, а на их создание.

Значение цвета выбирается как вектор, выходящий из центра окружности. Точка в центре соответствует белому цвету, а точки по периметру — чистым цветам. Направление вектора определяет цветовой, оттенок и задается в мо­дели НSВ в угловых градусах. Длина вектора определяет насыщенность цве­та. Яркость цвета задается на отдельной оси, нулевая точка которой имеет черный цвет.

Проще всего в компьютере реализуется модель RGB.

Это связано с мето­дом кодирования цвета байтами, поэтому создавать и обрабатывать цветные изображения принято в модели RGB. При печати рисунка RG В на цветном принтере драйвер принтера преобразует рисунок в цветовую модель СМYК.

Как уже отмечалось, режим представления цветной графики двоичным кодом из 24 разрядов называется полноцветным или Тruе Соloг. Очевидно, графические данные занимают очень большие объемы на носителях. Напри­мер, если экран монитора имеет растр 800x600 точек, изображение, пред­ставленное в режиме Тruе Со1ог, займет 800  × 600 × 3 = 1 440 000 байт.

В случае, когда не требуется очень высокое качество отображения цвета, применяется режим High Со1ог, который кодирует одну точку растра двумя байтами (16 разрядов дают 2¹⁶   ≈ 65.5 тысяч цветов).

Режим, который при кодировании одной точки растра использует один байт, называется индексным, в нем различаются 256 цветов. Этого недоста­точно, чтобы передать весь диапазон цветов. Код каждой точки при этом выражает собственно не цвет, а некоторый номер цвета из таблицы цветов, называемой палитрой. Палитра должна прикладываться к файлам с графиче­скими данными и используется при воспроизведении изображения.

Кодирование звуковой информации

Методы работы со звуковой информацией пришли в вычислительную техни­ку наиболее поздно. В итоге они далеки от стандартизации. Отдельные ком­пании разработали свои корпоративные стандарты, однако можно выделить два основных подхода.

Метод частотной модуляции( метод FМ —  Freguency Мodulation) осно­ван на разложении сигнала в виде суперпозиции элементарных гармоник с разными фазами, частотами и амплитудами. В природе звуковые сигналы имеют непрерывный спектр. Их разложение в гармонические ряды и представление в виде дискретных цифровых сигналов выполняют специальные устройства — аналого-цифровые преобразователи (АЦП).

Привоспроизведении происходит обратное преобразование — цифроаналоговое (ЦАП). Конструктивно АЦП и ЦАП находятся в звуковой карте компьютера. При таких преобразованиях неизбежны потери информации, связанные с методом кодирования. Метод компактен, но качество звучания не очень высоко и соответствует качеству звучания простейших электромузыкальных инструментов.

Метод таблично - волнового синтеза(Wawe - Тablе) заключается в том, ч образцы звуков для множества различных музыкальных инструментов (сэмплы) хранятся в особых таблицах. Числовые коды выражают тип инструмента, высоту тона, продолжительность и интенсивность звука, динамику его изменения и другие особенности. Затем при моделировании звуковой  информации эти образцы смешиваются. Качество звука, полученное в результате синтеза приближается к качеству звучания реальных музыкальных инструментов.

Структуры данных

В современных ЭВМ данные всегда велики по объему. Работать с ними проще, если данные упорядочены, т. е. образуют заданную структуру. Существует три основные типа структур: линейная, табличная и иерархическая.

Самая простая структура данных — линейная (список) — это упорядоченная структура, в которой адрес элемента однозначно определяется его номером. В качестве примера можно взять обычную книгу. При создании любой структуры данных надо решить, как разделять элементы данных между собой и как разыскивать нужные элементы. В качестве разделителя обычно используется какой-нибудь специальный символ.

Табличные структуры отличаются от списочных лишь тем, что элементы данных определяются адресом ячейки, который состоит не из одного параметра, как в списке, а из нескольких. В двумерных таблицах разделителей должно быть два. Таблица может быть и трехмерная, тогда три числа характеризуют положение элемента и требуются три типа разделителей, а может  быть и  n -мерная.

Нерегулярные данные, которые трудно представить в виде списка и таблицы, представляются иерархически. Иерархическую структуру имеет система почтовых адресов. В такой структуре адрес каждого элемента данных определяется путем доступа к нему (маршрута), ведущим от вершины структуры к данному элементу.

Каждый из описанных видов структур данных имеет свои преимущества  и недостатки. Например, списочные и табличные структуры являются простыми. Ими легко пользоваться, они легко упорядочиваются, однако их труд обновлять. При обновлении нарушается вся списочная или табличная струк­тура. Иерархические структуры данных сложнее, чем списочные или таблич­ные, но они не создают проблем с обновлением данных. Недостатком иерар­хических структур является относительная трудоемкость записи адреса элемента данных и сложность упорядочивания.

Файлы и файловая структура

В компьютерных технологиях единицей хранения: данных является объект переменной длины, называемый файлом. Файл— это последовательность произвольного числа байтов, обладающая уникальным именем. Файловые системы создают для пользователей некоторое виртуальное представление внешних запоминающих устройств ЭВМ, позволяя работать с ними не на низком уровне команд управления физическими устройствами, а на высоком уровне наборов и структур данных. Таким образом, файловая система — это система управления данными.    

Имя файла имеет особое значение —  оно фактически несет в себе адрес­ные функции в иерархических структурах. Кроме того, имя может иметь расширение, в котором хранятся сведения о типе данных. Если имена созда­ваемых файлов пользователь может задавать произвольно, то в использова­нии расширений следует придерживаться некоторой традиции.

Например, в операционной системе МSDOS файлы с расширениями: соm , ехе, bаt — исполняемые; bаt ,txt , do с — текстовые; раs, bas, с, fоr — тексты программ на известных языках программирования ( Паскале, Бейсике, Си, Фортране соот­ветственно ); дbf — файл базы данных.

В различных операционных системах существуют ограничения на длину имени и расширения имени файла.

 Так, в МS DOS длина имени файла не должна превышать восьми символов, а рас­ширение — трех, т. е. используется стандарт 8.3. В операционной системе Windowsограничения значительно менее жесткие.

Для пользователя файл является основным и неделимым элементом хра­нения данных, который можно найти, изменить, удалить, сохранить либо пе­реслать на устройство или на другой компьютер, но только целиком.

Файловая система — это часть операционной системы компьютера и по­этому всегда несет на себе отпечаток свойств конкретной операционной сис­темы. Файловая система скрывает от пользователя картину реального распо­ложения информации во внешней памяти, обеспечивает независимость программ от особенностей конкретной конфигурации ЭВМ, т. е. логический уровень работы с файлами. При работе с файлами пользователю предостав­ляются средства для создания новых файлов, операции по считыванию и записи информации и т. п., не затрагивающие конкретные вопросы программирования работы канала по пересылке данных, по управлению внешними устройствами.

Наиболее распространенным видом файлов, внутренняя структура которых обеспечивается файловыми системами различных операционных систем являются файлы с последовательной структурой. Файлы в этом случае представляются в виде набора составных элементов, называемых логическим записями произвольной длины и с последовательным доступом. В ряде операционных систем предусматривается использование более сложных логических структур файлов, например, древовидной структуры.

На физическом уровне блоки файла могут размещаться в памяти непрерывной областью или  храниться несмежно. Вся учетная информация о расположении файлов вмагнитном диске сводится в одно место — каталог или директорию диска. Каталог представляет собой список элементов, каждый из которых описывает характеристики конкретного файла, используемые дезорганизации доступа к нему — имя файла, его тип, местоположение на диске, размер. Каталогов может быть большое число, и они связываются в информационные структуры, например, в иерархическую (древовидную) систему каталогов. Каждый каталог рассматривается как файл и имеет собственное имя. Полное  имя каталога или файла в такой структуре задаёт путь переходов между каталогами и файлами в логической структуре каталогов.

Структура самих файлов может быть тривиальной. Например, текст может сохраняться в виде последовательности байтов, соответствующих кодировке таблицы АSСІІ. Однако в большинстве случаев вместе c данными приходится хранить и некоторую дополнительную информацию. Для реализации контроля возможных ошибок используются так назы­ваемые самокорректирующие коды, а по каналу связи вместе с псимволами основного сообщения передаются еще к дополнительных символов, обеспе­чивающих избыточность кодирования и позволяющих противодействовать
помехам.

Алгебра высказываний (алгебра логики)

Учение о высказываниях — алгебра высказываний или алгебра логики явля­ется простейшей логической теорией. Она рассматривает конечные конфигу­рации символов и взаимоотношения между ними.

Высказывание —  это всякое повествовательное предложение, утвер­ждающее что-либо о чем-либо, при этом непременно истинное или ложное. Логическими, значениями высказываний являются "истина" и "ложь", обо­значаемые  1  и 0. Высказывания, представляющие собой одно утверждение, называются простыми или элементарными, высказывания, получающиеся из элементарных с помощью грамматических связок "не", "и", "или", "если... то...", называются сложными. Эти названия не носят абсолютного характера, высказывания, которые в одной ситуации можно считать простыми, в другой ситуации будут сложными. В алгебре логики все высказывания рассматри­ваются только с точки зрения их логического значения, житейское содержа­ние игнорируется. Каждое высказывание может быть либо истинным, либо ложным, ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются строчными буквами латинского алфавита: а, b, с. Из высказываний с помощью логических связок образуются новые высказывания.

Рассмотрим наиболее употребительные логические связки.

Отрицанием высказывания х называется новое высказывание, которое является истинным, если высказывание   х ложно, и ложным, если х — ис­тинно. Обозначается х, читается "не х" или "неверно, что х".  Все логиче­ские значения высказывания х можно описать с помощью табл. 1.13. Если х — высказывание, то  х  — противоположное высказывание. Тогда можно образовать 0 , которое называется двойным отрицанием высказывания. Ло­гические значения 0, очевидно, совпадают со значениями х. Эта

операция одноместная — в том смысле, что из одного данного простого высказывания

х строится новое высказывание  .Х

Логическое умножение (конъюнкция). Конъюнкцией двух высказываний х и у называется новое высказывание z, которое истинно, только когда оба высказывания х и у истинны, и ложно, когда хотя бы одно из х и у ложно. Обозначается х & у или х^у,читается "х и у".

Из определения операции конъюнкции видно, что союз "и" в алгебре логики употребляется в том же смысле, что и в повсе­дневной речи. Однако в алгебре логики этой связкой можно связывать лю­бые, сколь угодно далекие по смыслу высказывания.  Конъюнкцию часто на­зывают логическим умножением.

Логическое сложение (дизъюнкция). Дизъюнкцией двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х и у истинно, и ложным, если они оба ложны. Обозначается          х v у, читается " х или у". 

Логические значения дизъюнкции описываются в табл. 1.13.

Таблица 1.13                                                                                                            Таблица 1.14



Импликация или логическое следование. Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, когда х истинно, а у ложно, и истинным во всех остальных случаях. Обозначается х → у, читается "если х, то у" или "из х следует у".

Высказывание х называется условием или поcылкой,  высказывание у  — следствием или заключением.

Из таблицы истинности видно, что если условие  х  — истинно, и истинна импликация  х → у, то верно и заключение у.

Это классическое правило вы­вода постоянно используется в математике, при переходе от одних высказы­ваний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.

В случае импликации несоответствие между обычным пониманием ис­тинности сложного высказывания и идеализированной точкой зрения алгеб­ры высказываний еще заметнее, чем для других логических операций. Здесь истинность импликации в некоторой ситуации означает лишь, что если в этой ситуации истинна посылка, то истинно и заключение.

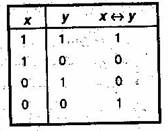
Эквиваленция (эквивалентность, логическая эквивалентность). Эквиваленцией двух высказываний  х и  у называется новое высказывание, которое истинно, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях.

Обозначается  х ↔ у, читается  “для того, чтобы  х, необходимо и достаточно, чтобы  у"  или  " х тогда и только тогда, когда у". Эквивалентность играет значитель­ную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.15.

Таблица 1.15



С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания.

Всякое сложное высказыва­ние, которое может быть получено из элементарных высказываний с помо­щью логических связок, называется формулой алгебры логики.

Формулы ал­гебры логики обозначаются большими буквами латинского алфавита А, В, С, ... Две формулы алгебры логики А и В  называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносиль­ность обозначается знаком  " ≡".

Для любых формул  А, В, С справедливы следующие равносильности.