Тожиев Мухриддин. Алгоритмы векторизации растрового изображения.. В современном мире информационные технологии тесно переплетены с нашей жизнью, другими отраслями и науками, и в данный момент мы как никогда зависим от плодов исследований и открытий в сфере информационных технологий

• Название: В современном мире информационные технологии тесно переплетены с нашей жизнью, другими отраслями и науками, и в данный момент мы как никогда зависим от плодов исследований и открытий в сфере информационных технологий
• Дата: 30.12.2018
• Размер: 394.98 Kb.
• Имя файла: Тожиев Мухриддин. Алгоритмы векторизации растрового изображения..docx
• Тип: Реферат; #62244

Содержание

ВВЕДЕНИЕ

В современном мире информационные технологии тесно переплетены с нашей жизнью, другими отраслями и науками, и в данный момент мы как никогда зависим от плодов исследований и открытий в сфере информационных технологий.

Одним из результатов исследований является цифровая графика, которая в свою очередь состоит из двух направлений: 1) растровойграфики 2) векторнойграфики. И проблема заключается в том, что изображения векторной и растровой графики имеют свои преимущества и недостатки относительно друг друга (которые будут изложены далее). Вследствие чего требуется переводить растровые изображения в векторный формат.

Векторизация (трассировка) — это ручное или автоматическое преобразование растрового изображения в его векторное представление. Благодаря такому преобразованию исходное изображение получает все преимущества векторной графики — малые размеры файла, возможность масштабирования и редактирования без потери качества. Технологии преобразования графических документов, полученных путем оцифровки традиционных источников – бумажных носителей, в векторную форму в настоящий момент являются весьма востребованными. Областью применения алгоритма могут быть пакеты графических редакторов (векторно-растровые) и различные геоинформационные системы (ГИС). Особенно актуален алгоритм векторизации именно для ГИС, так как процесс составления и формирования цифровых карт очень трудоемкий и, как правило, этот процесс ручного (экспертного) происхождения. Существуют множество алгоритмов векторизации растрового изображения, но они не универсальны, и каждая из них используются в определенных случаях. Сразу отметим, что на сегодняшний день пока нет алгоритмов векторизации, которыми можно перевести любое изображение автоматически без последующей ручной коррекции.

Целью курсовой работы является изучение и описание наиболее эффективных алгоритмы векторизации растрового изображения.

РАСТРОВАЯ ГРАФИКА

Растровые изображения состоят из мозаики точек, которая и носит название растр. Изображение на экране монитора или телевизора состоит из отдельных элементов – так называемых пикселов (от англ. PICture Single ELement –элемент изображения). В отличие от геометрической точки, пиксел имеет определенную форму (квадрат, круг, шестиугольник и т.п.) и размеры.

Растровое изображение характеризуется разрешением и количеством цветов, которое может принимать каждая точка изображения. Разрешение – это количество точек на единицу длины, обычно точек на дюйм – dpi (англ. dot per inch) или пикселов на дюйм – ppi (англ. pixel per inch).

Чем большим количеством оттенков характеризуется изображение, тем большее количество двоичных разрядов требуется для их описания. Таким образом, чем качественнее изображение, тем больше размер файла.

Растровое представление обычно используют для изображений фотографического типа с большим количеством деталей или оттенков.

Наиболее распространены следующие форматы растровых изображений: BMP, PCX, JPG, GIF, TIFF, PNG и др., они подробней будут рассмотрены ниже

Преимущества:

1. 
   Растровая графика позволяет создать практически любой рисунок, вне зависимости от сложности, в отличие, например, от векторной, где невозможно точно передать эффект перехода от одного цвета к другому без потерь в размере файла;
   
2. 
   Распространённость — растровая графика используется сейчас практически везде: от маленьких значков до плакатов;
   
3. 
   Высокая скорость обработки сложных изображений, если не нужно масштабирование;
   
4. 
   Растровое представление изображения естественно для большинства устройств ввода-вывода графической информации, таких как мониторы (за исключением векторных устройств вывода), матричные и струйные принтеры, цифровые фотоаппараты, сканеры, а также сотовые телефоны.
   

Недостатки:

1. 
   Большой размер файлов у простых изображений;
   
2. 
   Невозможность идеального масштабирования;
   
3. 
   Невозможность вывода на печать на векторный графопостроитель.
   

ВЕКТОРНАЯ ГРАФИКА

Основным логическим элементом векторной графики является геометрический объект. В качестве объекта принимаются простые геометрические фигуры (так называемые примитивы – точка, отрезок прямой или кривой линии, прямоугольник, окружность, эллипс), составные фигуры или фигуры, построенные из примитивов.

Для хранения векторного изображения в памяти достаточно сохранять лишь координаты основных точек и математическую формулу, согласно которой надо построить ту или иную фигуру. Именно поэтому векторные изображения отличаются малыми размерами файлов и их можно спокойно масштабировать, не опасаясь, что при этом потеряется качество изображения.

Наиболее распространенные форматы векторных изображений: CDR, EPS, WMF, AI и др.

Преимущества:

1. 
   Объём данных, занимаемый описательной частью, не зависит от реальной величины объекта, что позволяет, используя минимальное количество информации, описать сколь угодно большой объект файлом минимального размера. Например, описание окружности произвольного радиуса требует задания только 3 чисел, не считая атрибутов.
   
2. 
   В связи с тем, что информация об объекте хранится в описательной форме, можно бесконечно увеличить графический примитив при выводе на графическое устройство, например, дугу окружности, и она останется при любом увеличении гладкой. С другой стороны, если кривая представлена в виде ломанной линии, увеличение покажет, что она на самом деле не кривая.
   
3. 
   Параметры объектов хранятся и могут быть легко изменены. Также это означает что перемещение, масштабирование, вращение, заполнение и т. д. не ухудшает качества рисунка. Более того, обычно указывают размеры в аппаратно-независимых единицах (англ. Device-independent unit), которые ведут к наилучшей возможной растеризации на растровых устройствах.
   
4. 
   При увеличении или уменьшении объектов толщина линий может быть задана постоянной величиной, независимой от реальной площади изображаемой фигуры.
   

Недостатки:

1. 
   Не каждая графическая сцена может быть легко изображена в векторном виде — для подобного оригинальному изображению может потребоваться описание очень большого количества примитивов с высокой сложностью, что негативно влияет на количество памяти, занимаемой изображением и на время необходимое для преобразования его в растровый формат для графического вывода (отрисовки или растеризации).
   
2. 
   Перевод векторной графики в растровое изображение достаточно прост. Но обратный путь, как правило, сложен — этот процесс называют трассировкой растра, и зачастую требует значительных вычислительных мощностей и процессорного времени, и не всегда обеспечивает высокое качество полученного векторного рисунка.
   
3. 
   При этом спецификации векторных форматов (и, соответственно, рендереры векторной графики) намного сложнее таковых для растровой графики.
   
4. 
   Преимущество векторной картинки — масштабируемость — пропадает, когда векторный формат отображается в растровое разрешение с особо малыми разрешениями графики (например, иконки 32×32 или 16×16). Чтобы не было «грязи», картинку под такие разрешения приходится подгонять вручную. В векторных шрифтах TrueType есть довольно сложные коды хинтинга, позволяющие избавиться от пропущенных (и, наоборот, излишне толстых) линий
   

ВЕКТОРИЗАЦИЯ РАСТРОВЫХ ИЗОБРАЖЕНИЙ. ПРЕОБРАЗОВАНИЕ ХАФА.

Рассмотрим специализированное преобразование Хафа (Hough). Согласно методике, использующей это преобразование, на монохромном растровом изображении вместо декартовой системы координат вводится полярная (см. рис.3.1.) с координатами (ρ, θ).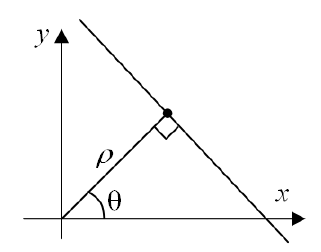



Рис.3.1. Переход к полярной системе координат

Прямая, проходящая через точку с координатами (x, y), будет определяться уравнением x⋅cosθ + y⋅sinθ = ρ. Функция, задающая семейство прямых, проходящих через эту точку, будет иметь вид F(ρ, θ, x, y) = x⋅cosθ + y⋅sinθ – ρ = 0. Через каждую точку (x, y) растрового изображения можно провести несколько прямых с разными ρ и θ (см. рис. 3.2.). Таким образом, каждой точке (x, y) соответствует некий набор точек в фазовом пространстве (ρ, θ), образующий синусоиду (см. рис. 3.3.). В свою очередь, каждой точке пространства (ρ,θ) соответствует набор точек (x, y) на изображении, образующий прямую. Каждой точке (ρ0, θ0) пространства (ρ, θ) можно поставить в соответствие счетчик, соответствующий количеству точек (x, y), лежащих на прямой x⋅cosθ0 + y⋅sinθ0 = ρ0.



Рис.3.2. Семейство прямых в декартовой системе координат



Рис.3.3. Семейство прямых в полярной системе координат



Рис.3.4. Единичная прямая в Декартовой системекоординат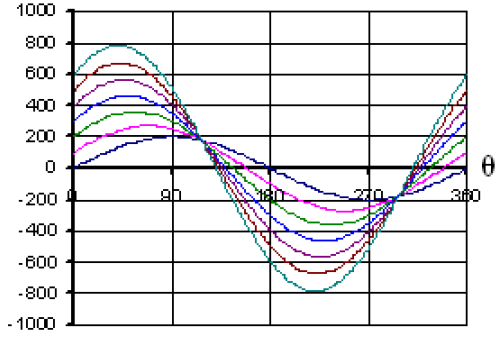



Рис.3.5. Единичный прямая в представлении набора синусоидов

Вследствие дискретности растрового представления исходного изображения каждой прямой в координатах (x, y) будет соответствовать не одна точка, а сгущение точек в координатах (ρ,θ).

Таким образом, достаточно выбрать на изображении, построенном в полярных координатах, самые «жирные пятна» и для их центров произвести преобразование в полярные координаты, получив тем самым параметры соответствующей прямой. Алгоритм преобразования Хафа приведен на рис. 3.6.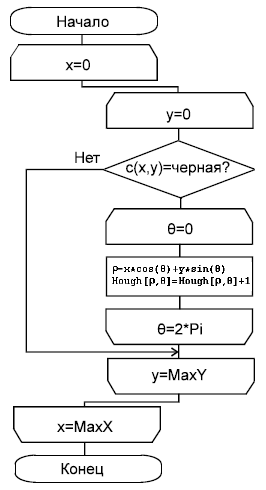



Рис.3.6. Алгоритм Хафа

Существуют также разновидности преобразования Хафа для дуг и окружностей. Таким образом, преобразование Хафа позволяет представить монохромное штриховое изображение в виде набора формул, описывающих прямолинейные и криволинейные элементы изображения, то есть произвести векторизацию этого изображения.

АЛГОРИТМЫ ВЕКТОРИЗАЦИИ ЦВЕТНЫХ РАСТРОВЫХ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ТРИАНГУЛЯЦИИ И ИХ РЕАЛИЗАЦИЯ

Нахождение граничных линий

Будем считать, что исходное растровое изображение (растр) состоит из пикселей, каждому из которых приписан некоторый цвет – целое положительное число (номер цвета). Граница между двумя совокупностями пикселей, окрашенных в два различных цвета, всегда проходит между пикселями, поэтому для построения граничных линий необходим вспомогательный растр – растр границ. Для его построения вначале расширим исходный растр G из M строк и N столбцов, дополнив его строками номер 0 и номер M + 1 и столбцами номер 0 и номер N + 1. Дополненным пикселям присвоим цвет номер 0. Затем сформируем растр границ B = {bij,uij} размером (M + 1)×(N + 1), элементы которого располагаются в узлах сетки, образованной точками расширенного растра G. Растр B определим по-другому, чем в [3]. Элемент bij растра B задает границы между четырьмя соседними пикселями различных (в общем случае) цветов {gi−1, j−1, gi−1, j , gi, j−1, gi, j}на растре G, а элемент uij – признак неудаляемой узловой точки. Вэлементе bij границы кодируются четырьмя битами следующим образом: если есть линия от центра вправо, то код: «1000»; если вверх – то код: «0100»; если влево – то код: «0010»; если вниз – то код: «0001». При нескольких линиях общий код образуется наложением кодов по операции «или». Если цвета у всех четырех пикселей одинаковы, то код равен нулю. Элемент uij = 1, если узловая точка в центре между четырьмя соседними пикселями есть, и uij = 0, если узловой точки нет. На рис. 4.1. показаны все возможные ситуации расположения различных цветов на соседних четырех пикселях растра G и соответствующие им значения кода bij и признака uij. Цифрами от 1 до 4 обозначены различные цвета.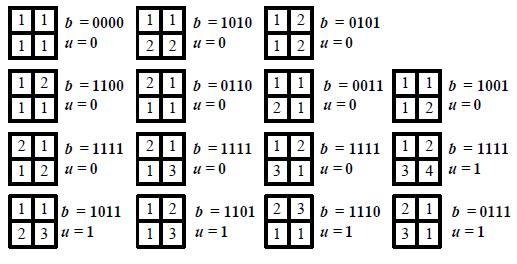



Рис.4.1.

Граничной линией назовем ломаную линию, образованную точками растра B, в которой: 1) соседние узлы этой ломаной являются 4-соседями на растре B; 2) при движении вдоль ломаной от начального узла до конечного слева и справа от всех отрезков ломаной находятся пиксели растра G двух различных цветов (слева одного, а справа –другого цвета); 3) ломаная является максимальной по включению.

Алгоритм 1. Выделение граничных линий.

1. Цикл по точкам растра B.

1.1. Если код bij очередной точки равен нулю,то переход к следующей очередной точке.

1.2. Иначе выполнение следующих действий:

1.2.1. Если признак uij = 0, то uij := 2.

1.2.2. Отслеживание граничной линии вплоть до точки с кодом upq > 0.

1.2.3. Если конечная (pq)-я точка совпадает с начальной (ij)-й точкой, то выделение граничной линии в виде замкнутой ломаной.

1.2.4. Иначе, если признак начальной точки uij = 2, то отслеживание линии от (ij)-й точки в обратном порядке.

Конец алгоритма.

При отслеживании линии алгоритм также запоминает цвет пикселей слева и справа от линии.

Алгоритм 1, сканируя точки растра B, находит ненулевой код bij и далее отслеживает очередную линию вплоть до точки с ненулевым признаком uij. При отслеживании в каждую точку brs растра B выполняется вход, а затем, если признак urs = 0, то выход. При входе и выходе обнуляются соответствующие биты в коде brs. Например, если при коде brs = «1111» вход был по линии слева от точки растра, а выход по линии вниз, то после этого код brs = «1100». Если признак urs > 0, то обнуляется только бит входа: brs = «1101». Если отслеживание граничной линии начинается с (ij)-й точки растра B, то обнуляется только бит выхода.

Просмотр точек в цикле на шаге 1 производится слева направо и сверху вниз, поэтому коды bij точек, с которых может начаться отслеживание граничной линии, могут быть только «1001», «1000» или «0001». Для кода «1001» направление отслеживания может быть любым, например вправо. При продолжении отслеживания в большинстве случаев проблемы неоднозначности не возникает, кроме некоторых вариантов с кодом «1111» (см. рис. 4.1.). Чтобы здесь решить, в каком направлении проходит диагональный участок линии в один пиксель, необходимо просмотреть предыдущее и последующее звено граничной линии. Выбрать следует тот вариант, который дает меньше поворотов в одном и том же направлении.

Нетрудно видеть, что алгоритм 1 каждую точку растра B просматривает от одного (для точки с кодом bij = «0000») до пяти раз (для точки с кодом bij = «1111»), т.е. его трудоемкость линейная от числа точек растра.

Отслеженная граничная линия может быть либо замкнутой, либо ограниченной в начале и конце узлами (точками растра B) с признаком uij = 1. На рис. 4.2. цифрами отмечены цвета пикселей растра G, буквами A, B, C и D – точки растра B, помеченные как узловые. Здесь шесть граничных линий построены соответственно между узлами: 1) A-B; 2) B-C; 3) B-D; 4) A-C; 5) A-D; 6) C-D, седьмая граничная линия замкнутая, она охватывает область пикселей с цветом 1.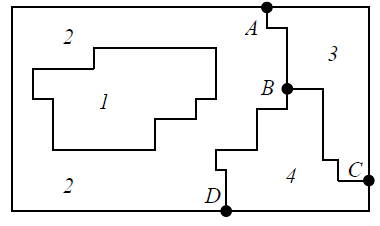



Рис.4.2.

Аппроксимация граничных линий прямолинейными отрезками

Полученные на предыдущем этапе граничные линии содержат чрезмерно большое число точек и выглядят ступенчатыми, поэтому их необходимо аппроксимировать. Рассмотрим аппроксимацию ломаными линиями, такими, что их отклонения от исходной граничной линии должны быть невелики, как правило, не более чем 1 пиксель. При этом также требуется, чтобы наиболее удаленные точки граничной линии отклонялись от аппроксимирующей ломаной по возможности на одинаковое расстояние по обеим сторонам. Приведенный в [3] способ аппроксимации может получить такой отрезок ломаной, что соответствующий участок исходной граничной линии располагается весь по одну его сторону. Поэтому рассмотрим еще один способ, лишенный указанного недостатка.

Алгоритм 2. Аппроксимация граничных линий.

1. Выделение и вставка характерных узловых точек (рис.4.3.).

1.1. Если граничная линия незамкнута, то выделяются две концевые точки.

1.2. Выделяются точки в углах – местах стыковки двух отрезков, если по длине оба строго больше чем 2 пикселя либо оба равны 2 пикселям.

1.3. Вставляются точки на отрезках длиной больше чем 2 пикселя, за 0.5 пикселя от места стыковки с другим отрезком длиной в 2 пикселя.

1.4. Вставляются точки в середине отрезков, являющихся локальными экстремумами, если на этих отрезках еще нет выделенных точек.

2. Вставляются точки в середине всех тех отрезков, на которых еще нет выделенных точек.

3. Удаляются те точки исходной граничной линии, которые остались не выделенными.

4. Просматриваются все получившиеся отрезки (по два соседних), и если наклон следующего строго совпадает с наклоном предыдущего, то удаляется промежуточная точка.

Конец алгоритма.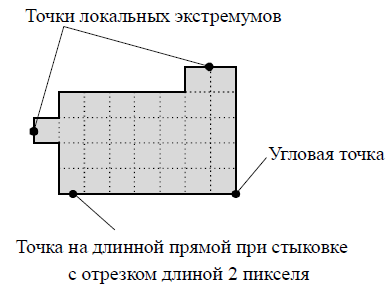



Рис.4.3.

Теорема. Алгоритм 2 строит аппроксимирующую ломаную с максимальным отклонением от исходной граничной линии менее 0.5 пикселя.

Доказательство. Введем следующие обозначения (рис. 4.4.): X – точка исходной ломаной; a, b – инцидентные точке X отрезки исходной граничной линии; N, M – середины отрезков a и b соответственно; d – сегмент аппроксимирующей линии; K, T – точки пересечения d с отрезками a и b соответственно. Длины отрезков a и b будем обозначать теми же буквами.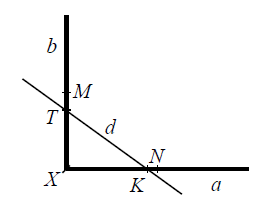



Рис.4.4.

Рассмотрим следующие случаи взаимного расположения отрезков исходной граничной линии и аппроксимирующей ломаной:

1. a > 2 и b > 2 либо a = 2 и b = 2. Точка X войдет в состав аппроксимирующей ломаной, поэтому отклонение равно нулю.

2. Длина одного из отрезков строго равна 2, длина другого больше чем 2 пикселя. Пусть для определенности a = 2 и b > 2. Тогда на отрезке b на расстоянии 0.5 пикселя от точки X будет добавлена узловая точка, через которую пройдет аппроксимирующая ломаная. Очевидно, что расстояние от точки X до этой ломаной не больше 0.5 пикселя.

3. Длина одного из отрезков, например a, равна единице. Тогда K находится на расстоянии 0.5 от точки X, а евклидово расстояние от точки X до отрезка d – менее 0.5 пикселя.

Теорема доказана.

При реализации рассмотренного алгоритма для хранения данных необходима дискретность представления координат, равная 0.5 пикселя. Это требование легко выполняется в рамках целочисленной арифметики – достаточно хранить координаты удвоенными.

Алгоритм 2 строит весьма точную аппроксимацию, однако в некоторых случаях она может оказаться излишне детальной. Если допустить максимальное отклонение аппроксимирующей ломаной больше чем 0.5 пикселя, то в алгоритме 2 можно выполнить еще один – дополнительный шаг аппроксимации. На этом шаге просматриваются соседние отрезки и проверяется возможность их склеивания – отбрасывания соединяющей их узловой точки. Узловая точка отбрасывается, если: 1) она вставлена на шаге 2 в середину какого-либо отрезка; 2) максимальное отклонение склеенного отрезка от исходной граничной линии не превышает заданной величины Δ (0.5 < Δ ≤ 1). Очевидно, что при этом максимальное отклонение не будет превышать Δ. При отбрасывании промежуточных узловых точек необходимо контролировать длины получающихся отрезков так, чтобы отношение длин соседних отрезков на границе не превышало величину 5–10. Это необходимо для того, чтобы облегчить последующую обработку, в частности триангуляцию.

Распознавание объектов на триангуляции

Следующим этапом работы является построение триангуляции Делоне с ограничениями. В качестве ребер ограничений выступают отрезки аппроксимирующих ломаных, полученные на предыдущем шаге. Эта задача на практике решается с помощью известных алгоритмов за время O(n log n) в наихудшем илиза O(n) в среднем [4, 5]. При построении триангуляции каждое из ребер треугольников помечается либо как отрезок аппроксимирующей ломаной (и тогда для него запоминается цвет пикселей слева и цвет справа), либо как «невидимое» ребро.

Далее в построенной триангуляции выделяются области, состоящие из треугольников одинакового цвета (методом «заливки с затравкой», см. [5]).

Выделенные одноцветные области необходимо классифицировать на линейные и площадные. В работе [3] эта задача решается построением скелета (серединной линии) внутри области. Для этого первоначально скелет строится внутри каждого из треугольников, который затем сшивается в связный граф. При этом для каждого треугольника оценивается толщина объекта, которая и позволяет классифицировать этот объект как линейный (с толщиной меньше заданной величины) либо как площадной.

В работе [3] для оценивания толщины рассматриваются пары треугольников, имеющих общее невидимое ребро. Однако возможны ситуации (если оба треугольника сильно вытянуты и к тому же тупоугольные), когда оценка толщины оказывается некорректной. Используем более простой и надежный способ – вычисление отношения площади области к суммарной длине ребер ограничений, входящих в область. Последующее более точное измерение толщины объекта будем производить лишь для тех треугольников, которые на первом этапе помечены как линейные.

Рассмотрим идеальный случай: отрезок прямой, образованный двумя параллельными граничными отрезками длиной по L (рис. 4.5.). Треугольник abc содержит одно ребро ограничения ab длины L. Высота треугольника равна d – ширине линии. Площадь треугольника Sabc и участка линии Sлинии связаны соотношением линии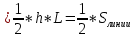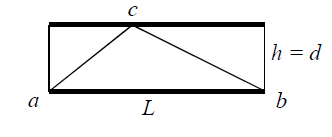




Рис.4.5.

Аналогичные соотношения выполняются с некоторыми погрешностями и для случаев типа изображенных на рис. 4.6., когда вычисляется средняя ширина линии для группы треугольников (при этом площадь внутреннего треугольника А также должна быть учтена).

Таким образом, можно сформулировать следующий критерий: если площадь группы треугольников меньше половины произведения суммарной длины ребер ограничений на максимально возможную ширину линии, то треугольники считаются линейными. Как показывают вычислительные эксперименты, применение этого критерия к группе треугольников дает более качественные результаты, чем к отдельным треугольникам.



Рис.4.6.

При этом предлагается формировать группы из треугольников внутри одноцветной области, смежных с общей для них опорной вершиной. Из нескольких подряд расположенных вдоль границы вершин в качестве опорной следует выбирать ту, которая является смежной не менее чем с тремя треугольниками. Кроме того, при этом следует учесть особые случаи, когда вся одноцветная область состоит из одного или двух треугольников. В процессе анализа одноцветной области отдельные треугольники могут поочередно попасть в две-три группы, что увеличивает вероятность того, что они будут классифицированы правильно. Некоторый треугольник классифицируется как площадной, если он поочередно помещался в несколько групп, и хотя бы одна из них была классифицирована как площадная. В противном случае треугольник классифицируется как линейный.

На рис. 7 одноцветная область изображена черным цветом. На рис. 8 показан результат работы алгоритма классификации объектов. Черным цветом изображены треугольники, классифицированные как линейные, серым – как площадные.



Рис.4.7.



Рис.4.8.

Недостатком данного алгоритма является то, что иногда треугольники на границе площадных объектов принимаются алгоритмом за линейные объекты. Для исправления ошибок данного типа производится дополнительная проверка – с помощью дополнительного просмотра триангуляции все линейные треугольники, у которых длина невидимого ребра больше максимальной ширины линии, и которые соседствуют по невидимому ребру с площадным треугольником, считаются ошибочно классифицированными как линейные, и помечаются как площадные. Трудоемкость данного этапа – линейная относительно числа точек в триангуляции, так как число треугольников линейно зависит от числа точек.

Создание векторной модели растра

Результатом работы алгоритмов предыдущих этапов является полностью размеченная триангуляция, которая содержит достаточную информацию для построения векторной модели растра. Дальнейшие действия, описанные в работе [3], проиллюстрированы, в частности, на рис. 9.

При создании векторного представления линейных объектов отслеживаются смежные линейные треугольники одного цвета с одновременным построением скелетной линии. Линейные треугольники можно условно разделить на три типа: «внутренние» (все ребра невидимые), «боковые» (одно ребро границы и два невидимых ребра), «оконечные» (одно невидимое ребро и два ребра границы). Алгоритм в процессе работы строит участки скелетных линий, проходящих через середины невидимых ребер «боковых» треугольников и заканчивающихся в точке пересечения медиан, если последний треугольник линии – «внутренний», либо в точке пересечения ребер ограничений, если последний треугольник линии – «оконечный», либо на середине открытого ребра, если последний треугольник данного участка скелетной линии – «боковой». На рис. 4.9. эти случаи соответственно обозначены цифрами 1, 2, и 3.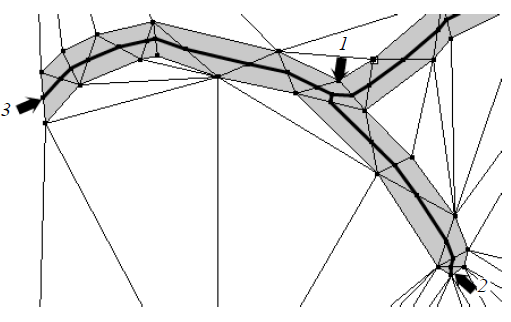



Рис.4.9.

После этого фильтруются некоторые погрешности скелетных линий, а оставшиеся их смежные участки склеиваются. При этом распознается ситуация, когда стыкуются две распознанные линии разной толщины. Для создания векторных представлений площадных объектов строятся максимальные по включению связные области, состоящие только из треугольников, не являющихся линейными. При этом строится внешняя граница площадного объекта. Нетрудно видеть, что трудоемкость каждого из рассмотренных этапов – линейная относительно числа треугольников.

Аппроксимация площадных векторных объектов кривыми Безье

Векторная модель растра, построенная рассмотренным выше алгоритмом, представляет собой наборы ломаных и многоугольников. Однако во многих задачах иллюстративной графики и дизайна требуется представлять векторные объекты плавными кривыми, в качестве которых используются, как правило, кривые Безье [4]. При этом обычно ставится задача построения только площадных объектов (без распознавания линий на растре).

Пусть на растре B алгоритмом 1 выделен набор граничных линий, каждая из которых является либо замкнутой, либо нет, и тогда она имеет начальную и конечную точки. Кроме того, для каждой линии задана ориентация и запомнены цвет области слева и цвет области справа.

Построение площадных объектов по граничным линиям можно выполнить без построения триангуляции. Для этого необходимо построить планарный ориентированный граф, в котором каждая граничная линия – ребро, а точки сочленения граничных линий – вершины графа. Кроме того, в каждой вершине указывается порядок смежных с вершиной ребер по направлению часовой стрелки.

По такому графу легко совершить обход по всем контурам, ограничивающим одноцветные области, выделив таким образом площадные объекты.

Теперь рассмотрим задачу аппроксимации граничных линий кривыми. Каждую такую линию будем аппроксимировать следующим образом.

Алгоритм 3. Аппроксимация граничных линий кривыми Безье.

1. Формирование списка характерных узловых точек.

1.1. Если граничная линия незамкнута, то в список заносятся две концевые точки линии.

1.2. В список заносятся точки в углах линии – местах стыковки двух отрезков, если они по длине оба больше, чем некоторая заданная величина δ (в пикселях).

1.3. В список заносятся точки в середине тех отрезков линии, которые являются локальными экстремумами, если на этих отрезках еще нет точек, занесенных в список.

2. Цикл по списку характерных узловых точек (кроме концевых).

2.1. Для k точек исходной граничной линии слева от узловой точки вычисляется наклон аппроксимирующей прямой, проходящей точно через узловую точку и в среднем вблизи k точек.

2.2. Вычисляется наклон аналогичной аппроксимирующей прямой для k точек справа.

2.3. Если наклоны аппроксимирующих прямых слева и справа различаются более, чем на заданный угол ε, то запоминаются оба наклона для этой узловой точки.

2.4. В противном случае вычисляется наклон ппроксимирующей прямой для k точек слева и для k точек справа и запоминается общий наклон для этой узловой точки.

3. Для концевых узловых точек (если они есть) вычисляется наклон аппроксимирующей прямой, проходящей точно через узловую точку и в среднем вблизи k соседних точек.

4. Цикл по списку характерных узловых точек (рассматриваются по две соседних точки).

4.1. Строится отрезок аппроксимирующей кривой Безье 3-й степени по двум узловым точкам и по наклонам слева и справа.

4.2. Если максимальное отклонение кривой Безье от соответствующего участка граничной линии превышает заданную величину Δ, то в середину этого участка вставляется новая узловая точка и вычисляется для нее наклон аппроксимирующей прямой для k точек слева и для k точек справа.

Конец алгоритма.

Так как некоторые характерные узловые точки имеют координаты, кратные 0.5 пикселя, то все расчеты следует вести на целочисленной сетке с шагом 0.5 пикселя. Вычисление наклона аппроксимирующей прямой, проходящей через узловую точку, можно вести методом наименьших квадратов. Пусть параметрическое уравнение аппроксимирующей прямой в системе координат с нулем в узловой точке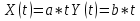



Пусть также параметр t на соседних точках граничной линии (на целочисленной сетке) имеет значения 1, 2, …, k справа от узловой точки и, соответственно, –1, –2, …, – k слева от узловой точки. Если минимизировать сумму квадратов расстояний между этими точками (xi, yi) и соответствующими точками прямой (1) – (X(ti), Y(ti)), то получим следующие оценки коэффициентов наклона a и b: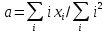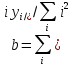

,

Для построения отрезка кривой Безье 3-й степени по двум узловым точкам и по наклонам слева и справа необходимо от наклонов перейти к управляющим точкам. Следует учесть, что отрезок кривой Безье есть локальный параметрический сплайн, заданный полиномами X(t) и Y(t) третьей степени, где параметр t изменяется от 0 до 1. В работе [5] приведен способ нормализации такого сплайна вдоль длины кривой, позволяющий рассчитать длины касательных в точках при t = 0 и t = 1 таким образом, чтобы кривая была наиболее выпуклой.

Проверку максимального отклонения отрезка кривой Безье от соответствующего участка граничной линии можно выполнить с помощью быстрого алгоритма цифровой интерполяции параметрических полиномов [6].

Следует заметить, что некоторый отрезок кривой Безье может на самом деле оказаться прямолинейным, если линии наклона для двух соседних узловых точек направлены строго вдоль отрезка, их соединяющего. На рис. 10 показан процесс аппроксимации граничных линий отрезками кривой Безье, а на рис. 11 – пример построения площадных объектов и аппроксимация граничных линий этих объектов.

БЫСТРЫЙ АЛГОРИТМ ВЕКТОРИЗАЦИИ БИНАРНЫХ ШТРИХОВЫХ ИЗОБРАЖЕНИЙ

Построение графовой модели

Итак, пусть растр представлен в сжатой форме REE (Run Ends Encoding) [3]. Опишем основные шаги алгоритма построения графовой модели. Выделяются связные компоненты(СК) изображения, затем для каждой СК выполняется быстрый алгоритм частичной скелетизации, основной задачей которого является нахождение средних линий объектов прямолинейной формы. Средние линии представляются скелетными кривыми (СКР). Известным недостатком большинства алгоритмов скелетизации является недостаточно точная обработка мест соединений. Совершенно очевидно, что последующая векторизация даст в таком случае ощутимую погрешность. Нами предлагается быстрая обработка "простых" участков и аналитическая — "сложных". Алгоритм состоит из двух проходов. В каждом проходе изображение сканируется вертикальными строками и анализируется связность смежных серий. Последовательность смежных серий, в которой отсутствуют случаи ветвления и слияния серий, будет называться полосой. При работе с каждой скан-строкой изображения добавляются серии к имеющимся полосам. После того, как полосы сформированы, вычисляются их средние линии, которые являются СКР. При сканировании вертикальными строками будут обработаны области, имеющие горизонтальную направленность. Для того, чтобы обработать вертикальные объекты, изображение поворачивается на 90º и выполняется скан-проход алгоритма.

Произведем сравнительный анализ некоторых распространенных алгоритмов утоньшения с предлагаемым алгоритмом частичной скелетизации.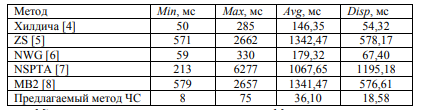



Таблица 5.1. Сравнение производительности алгоритмов утоньшения

Примечания. Min — минимальное время утоньшения, Max — максимальное время утоньшения, Avg — среднее выборочное время утоньшения, Disp — квадратный корень среднеквадратичного отклонения времени утоньшения.

Высокая производительность алгоритма частичной скелетизации обуславливается тем, что он анализирует смежные серии. Алгоритм оставляет необработанными области пересечений и соединений, которые обрабатываются отдельно классическим алгоритмом попиксельного утоньшения. Каждая область соединения (ОС) представлена множеством серий. Из области соединения исходят СКР, аппроксимирующие относительно прямолинейные участки. Для каждой СКР, исходящей из ОС, получим вектор направления, построенный по ее начальным точкам. Найдем точку пересечения векторов направлений ОС и соединим ее отрезками с начальными точками СКР. Пометим точки растра, через которые проходят эти отрезки. Затем применим параллельный алгоритм утоньшения для ОС, который не будет удалять помеченные пиксели. Таким способом обеспечивается корректная обработка соединений. На следующем шаге анализом последовательности серий единичной ширины выделим группы серий, удовлетворяющие условиям СКР. Заменим эти серии с помощью СКР. В данном случае СКР будет являться альтернативным способом представления последовательности пикселей единичной толщины. Перейдем к построению графовой модели. По координатам узловых серий (т.е. серий, которые указывают на СКР) сформируем множество вершин V. По точкам СКР построим ребра. Каждая СКР была прикреплена к двум узловым сериям, которые преобразовались в вершины, следовательно, можно найти вершины, из которых исходят ребра. Рассмотрим два смежных ребра. Если они являются коллинеарными (допускается погрешность в 5°), то они могут быть заменены одним ребром.

В результате вышеописанных действий каждая СК изображения представляется нагруженным ориентированным планарным псевдографом, вершинам которого соответствуют концевые и узловые точки отрезков СК, а ребрам — сами отрезки СК, представленные в форме СКР. Независимые подходы к описанию и построению графовых моделей были предложены в [9–11].

Граф G задается парой G=(V, E), где V — множество вершин. Описание каждой вершины содержит координаты точки, порядок вершины и ее тип (концевая или узловая); E — мультимножество ребер, каждое из которых соединяет две вершины из V, причем изображения ребер из E на плоскости не пересекаются, поэтому (V, E) представляет собой планарный граф. Каждое ребро имеет важные характеристики (например: длина, ширина, элонгация), которые могут быть использованы при последующем создании векторной модели. Т.е. выделенные на этапе векторизации объекты могут быть снабжены соответствующими атрибутами

Граф может быть преобразован в более компактную форму гиперграфа, гиперребра которого состоят из ребер, соединяющих вершины степени 1 и 2 исходного графа (рис. 1).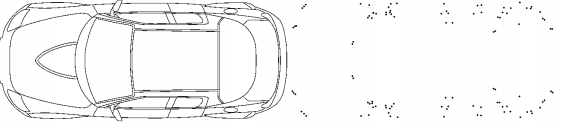



Рис.5.1. Пример графовой модели, исходное изображение и узлы гиперграфа

Нахождение путей векторизации

Для последующей постобработки поместим узловые и концевые точки в отдельные массивы [12] (МУТ, МКТ). Следующим шагом является построение векторной модели на основании имеющегося графа. Из имеющегося псевдографа G получим гиперграф GG. На первом шаге процедуры построения выделим гиперребра графа GG, состоящие из ребер графа G, соединяющих вершины графа G степени один и два. Каждое гиперребро имеет две концевые вершины. Из каждой такой вершины гиперребра GE исходит ноль или более одного ребра E, не принадлежащих гиперребру GE. Рассмотрим 2 ребра E1 и E2, исходящих из вершины степени 3 графа G. Пусть ребра E1 и E2 принадлежат гиперребрам GE1 и GE2 соответственно. Если ребра E1 и E2 являются коллинеарными с некоторой погрешностью (например, 5°), то гиперребра GE1 и GE2 объединяются.

Введем понятие пути векторизации. Под путем векторизации (ПВ) будем понимать последовательность точек pi=(xi , yi), лежащих на средней линии СК. ПВ={p0, p1, …, pn}. Если p0=pn, то путь является закрытым. Точки ПВ описывают набор отрезков и дуг окружностей. Каждое гиперребро описывает ПВ (рис. 5.2.).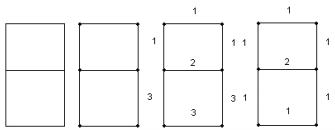



Рис.5.2.

Выделение отрезков прямых

В зарубежной литературе генерализация называется полигонализацией и полигональной аппроксимацией. Полигональная аппроксимация является средством компактного и эффективного представления линий для анализа формы и классификации образов. Она позволяет сократить количество входных данных и сгладить незначительные искажения линий. Оптимальное представление линии должно иметь некоторые из следующих свойств. Во-первых, оно должно хорошо сохранять информацию, т.е. все существенные особенности формы не должны устраняться. Во-вторых, оно не должно использовать значительных объемов памяти. В-третьих, представление должно быть нечувствительно к локальным шумам и преобразованиям, таким как параллельный перенос, поворот, масштабирование и т.д.

Введем понятия сегмента. Под сегментом будем понимать прямолинейный отрезок, полученный путем полигональной аппроксимации точек пути векторизации. Нами реализовано несколько алгоритмов выделения линий. Классическим методом для выделения отрезков является метод генерализации Дугласа–Пекера [13]. Этот метод является итерационной аппроксимацией от концевых точек. Пусть имеется путь векторизации ПВ={p0, p1, …, pn}. Рассмотрим процедуру аппроксимации. Построим отрезок p0pn. Пусть pk — самая удаленная от отрезка p0pn вершина. Если расстояние от pk до отрезка p0pn меньше заданного порога, то p0pn аппроксимирует последовательность. В противном случае разобьем ПВ на две части: P1={p0, …, pk} и P2={pk+1,…, pn}. Для каждой части рекурсивно применяется процедура аппроксимации. Возможно использование следующей модификации алгоритма. Пусть имеется путь векторизации ПВ={p0, p1, …, pn}. Построим нормированный вектор 0 , n p p . Развернем его на 90º против часовой стрелки. Для каждой точки pi построим вектор 0 , , 0.. i p p i n . Рассчитаем скалярное произведение 0 0 ( , , , ) i n p p p p , которое будет характеризовать отклонение вектора 0 , i p p от 0 , n p p . Будем накапливать значения положительного и отрицательного отклонений. После того как отклонения рассчитаны, определяются среднее DAver и максимальное DMax значения отклонений. Если DAver превышает пороговую величину среднего отклонения, умноженного на толщину отрезка, то ПВ не может быть представлен одним отрезком. Аналогично, если DMax превышает пороговую величину максимального отклонения, умноженного на толщину отрезка, то ПВ не может быть представлен одним отрезком. В таком случае ПВ разбивается на две равные части, каждая из которых аппроксимируется отдельно.

Штриховые технические изображения содержат большое количество горизонтальных, вертикальных и диагональных линий. Для их выделения на первом, предварительном этапе полигональной аппроксимации, предлагается следующая методика. Вводятся 4 направляющих вектора, описывающих направления линий: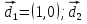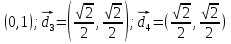

=

Последовательно рассматривается каждый направляющий вектор i d . Повернем вектор i d на 90º против часовой стрелки, обозначим результат через n i d . В качестве опорной точки b выбирается первая точка ПВ. "Плавающей" точкой f является вторая точка ПВ. По этим двум точкам строится вектор K . Вычисляется скалярное произведение векторов K и n i d . Как известно, скалярное произведение ортогональных векторов равно нулю. Если скалярное произведение равно нулю, в качестве "плавающей" точки выбирается следующая точка ПВ. Если условие не выполняется, процедура повторяется для следующего направляющего вектора.

На следующем этапе полигональной аппроксимации выделяются оставшиеся прямолинейные отрезки. Применяется модификация алгоритма Склански и Гонсалеса последовательного пересечения углов на плоскости. Данная методика является аппроксимацией от одной начальной точки. Алгоритм, предложенный в работе [14], использует следующую процедуру нахождения очередной критической точки. В начале вокруг следующей точки из исходного набора строится окружность радиуса ε и проводятся два луча, выходящие из текущей критической точки, касающиеся данной окружности, образующие угол выбора. Затем, для каждой последующей точки из исходного набора аналогично строится угол, касающийся окружности радиуса ε, проведенной вокруг этой точки, и находится пересечение этого угла с текущим углом выбора. Если данное пересечение пусто, то последняя точка, попавшая в угол выбора, объявляется критической и процедура повторяется для нее. Иначе вычисленное пересечение используется как угол выбора для следующих точек исходного набора. Нами предлагается следующая эффективная реализация алгоритма. Сначала выбирается опорная точка, т.е. точка, от которой происходит аппроксимация. Опорная точка определяется с помощью анализа массива сегментов, выделенных на первом этапе. Если массив пуст, то в качестве опорной точки b полагается первая точка ПВ, в противном случае выбирается точка, не принадлежащая выделенному сегменту. Пусть опорная точка имеет индекс bi в массиве точек ПВ. "Плавающей" точкой f считается следующая точка ПВ, т.е. точка с индексом fi=bi+1. По этим двум точкам строится текущий вектор направления K . Повернем вектор K на 90º против часовой стрелки, обозначим результат через N . Построим четыре вектора Ci , отклоняющихся от K на заданную константу(в данной работе 0,5)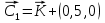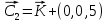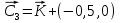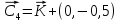









Рассчитаем скалярное произведение векторов Ci и N , определим минимальное и максимальное значения скалярного произведения. Два вектора CL и CR , скалярное произведение с которыми вектора N дало экстремальные значения, будут формировать начальный угол выбора. Назовем эти вектора "конусом". На следующей итерации на единицу увеличивается fi , выбирается новая "плавающая" точка. Строится вектор направления K , соединяющий опорную и "плавающую" точки. Определяется текущее значение угла выбора. Вычисляется новое значение "конуса" как пересечение векторов текущего "конуса" и "конуса", полученного на предыдущей итерации. Т.е. на каждой итерации "конус" будет сужаться. Алгоритм продолжает свою работу до тех пор, пока "конус" не вырождается в прямую. Следует отметить, что данный алгоритм является эффективным, так как его трудоемкость линейна относительно количества исходных точек.

Выделение дуг окружностей

Согласно имеющимся исследованиям [15], существуют два основных семейства алгоритмов выделения дуг окружностей. Первое семейство основано на модификациях преобразования Хафа (ПХ). Данные алгоритмы работают с пикселами изображения напрямую. Они достаточно хорошо изучены и обладают высоким качеством распознавания при работе с зашумленными изображениями. Однако использование ПХ требует большого количества вычислений, имеется квадратичная зависимость трудоемкости от точности распознавания, серьезным недостатком является недостаточно точное нахождение центра и начальных точек дуги окружности. Второе семейство алгоритмов работает с последовательностью сегментов, являющихся результатом процедуры полигональной аппроксимации. С помощью анализа смежных сегментов определяются параметры дуги окружности.

Итак, пусть результатом имеется результат генерализации, представленный сегментами S1, S2, …, Sn. Для правильного выделения дуги окружности требуется, чтобы сегменты полилинии достаточно точно аппроксимировали дугу. Во-первых, полилиния должна иметь одинаковую кривизну, т.е. каждый последующий сегмент должен поворачивать по отношению к предыдущему либо по часовой, либо против часовой стрелки. Во-вторых, все сегменты полилинии должны иметь примерно одинаковую толщину. В-третьих, точки средней линии найденных сегментов должны принадлежать дуге окружности, т.е. должны выполняться условия: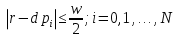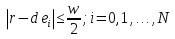





где r — радиус дуги; w — толщина полилинии; dpi — расстояние от центра дуги до i-й узловой точки полилинии; dei — расстояние от центра дуги до i-го сегмента полилинии; N — число сегментов полилинии.

Из Евклидовой геометрии известно, что три неколлинеарные точки X, Y, Z на плоскости однозначно определяют окружность. Центр окружности U будет находиться на пересечении перпендикуляров, опущенных на середины отрезков XY и YZ. Рассмотрим пару смежных сегментов SiSi+1. В качестве точки Х возьмем первую точку сегмента Si, , в качестве точки Z возьмем последнюю точку сегмента Si+1. Таким образом сформирован набор точек ПВ, который может быть аппроксимирован дугой окружности. В качестве точки Y выбирается точка ПВ, находящаяся в массиве ПВ на равном расстоянии от X и Z. Вычисляется центр дуги и радиус. Рассчитывается отклонение точек сегментов SiSi+1 от уравнения дуги окружности. Если все условия выполнены, то дуга найдена. Затем итеративно осуществляются попытки продолжения дуги. Так как дуга имеет две концевые точки, существуют два направления расширения дуги. В каждой итерации к сегментам, образовавшим дугу, добавляется новый сегмент. Определяется новый центр и радиус, осуществляется проверка корректности.

Полученные из сегментов отрезки и дуги окружностей получают характеристику ширины ребра графа G, из анализа которого они были получены.

В качестве постобработки предлагается стыковка отрезков в местах соединений. Это осуществляется анализом МУТ и МКТ.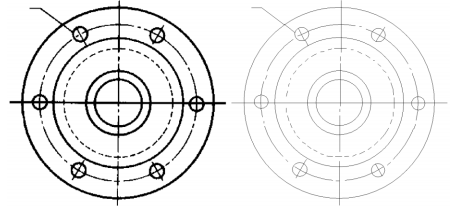



Рис.5.3. Пример исходного изображения и результат векторизации

ЗАКЛЮЧЕНИЕ