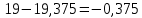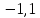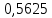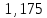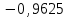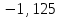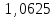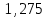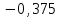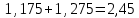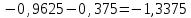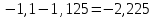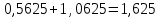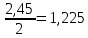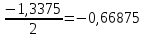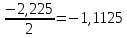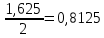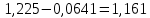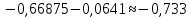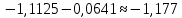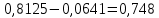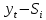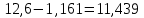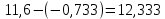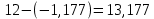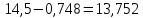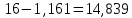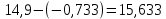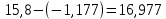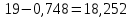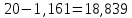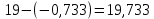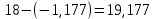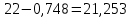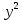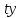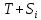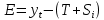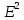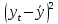Математика. 1 вариант. В таблице указан объем продаж (тыс руб.) за последние 12 кварталов
 Скачать 70.8 Kb. Скачать 70.8 Kb.
|
|
ВАРИАНТ 1 Практическое заданиеВ таблице указан объем продаж (тыс. руб.) за последние 12 кварталов. Требуется построить график, аддитивную модель временного ряда и сделать прогноз на следующие 4 квартала:
Решение Построим аддитивную модель. Общий вид аддитивной модели следующий: 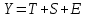 Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой ( 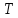 ), сезонной ( ), сезонной (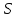 ) и случайной ( ) и случайной (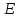 ) компонент. ) компонент. Рассчитаем компоненты аддитивной модели временного ряда. Произведем выравнивание исходных уровней ряда методом скользящей средней. Таблица 1
Произведем оценку сезонной компоненты. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Для данной модели имеем: 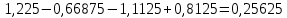 Корректирующий коэффициент: 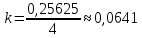 Рассчитываем скорректированные значения сезонной компоненты 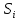 и заносим полученные данные в таблицу. и заносим полученные данные в таблицу. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины 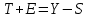 . Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту. . Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Найдем уравнение тренда для определения трендовой компоненты: 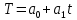 Параметры уравнения 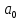 и и 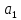 определим при помощи системы двух нормальных уравнений, отвечающих требованию метода наименьших квадратов: определим при помощи системы двух нормальных уравнений, отвечающих требованию метода наименьших квадратов: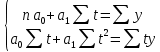 Построим таблицу предварительных расчетов:
Для наших данных система уравнений имеет вид: 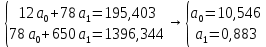 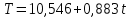 Теперь произведем элиминирование влияния сезонной компоненты 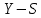 , определим трендовую , определим трендовую 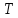 и случайную и случайную 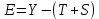 компоненты. компоненты.Вычисления произведем в таблице:
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок. 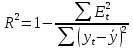 Среднее значение: 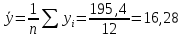
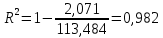 Следовательно, можно сказать, что аддитивная модель объясняет 98,2% общей вариации уровней временного ряда. Прогнозирование по аддитивной модели. Прогнозное значение 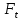 уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда: уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда: 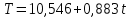 Получим 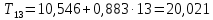 Значение сезонного компонента за соответствующий период равно 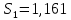 Таким образом, 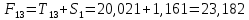 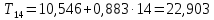 Значение сезонного компонента за соответствующий период равно: 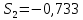 Таким образом, 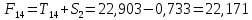 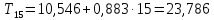 Значение сезонного компонента за соответствующий период равно: 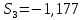 Таким образом, 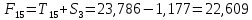 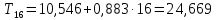 Значение сезонного компонента за соответствующий период равно: 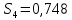 Таким образом, 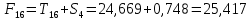 Изображение временного ряда и тренда: 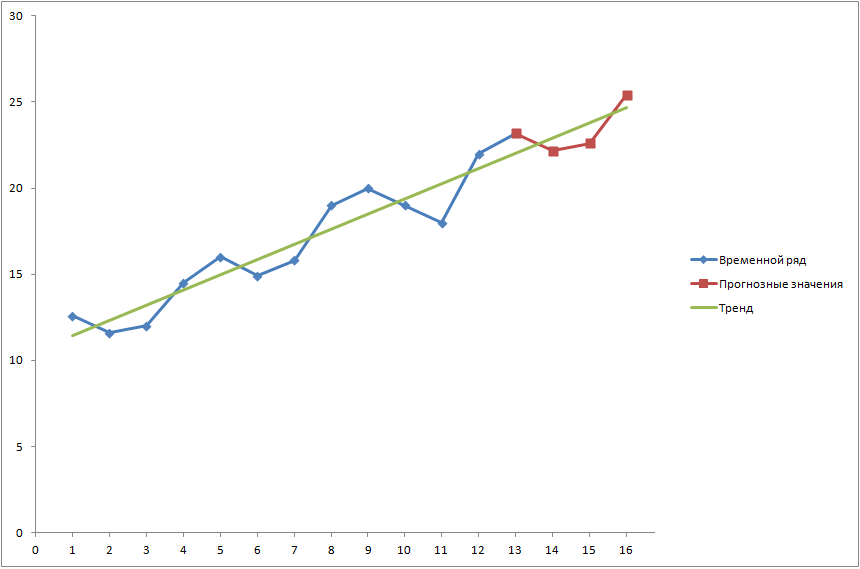 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

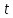
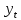
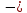
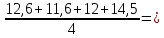 12,675
12,675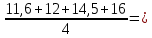 13,525
13,525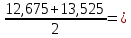 13,1
13,1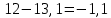
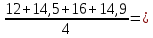 14,35
14,35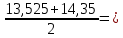 13,9375
13,9375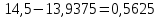
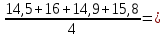 15,3
15,3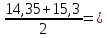 14,825
14,825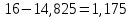
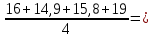 16,425
16,425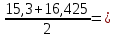 15,8625
15,8625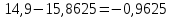
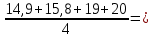 17,425
17,425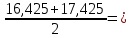 16,925
16,925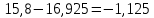
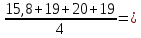 18,45
18,45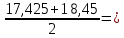 17,9375
17,9375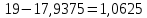
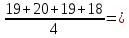 19
19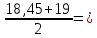 18,725
18,725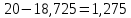
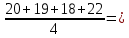 19,75
19,75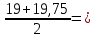 19,375
19,375