Статистика (1). Вариация как свойство массовых явлений

• Название: Вариация как свойство массовых явлений
• Дата: 02.04.2023
• Размер: 317.5 Kb.
• Имя файла: Статистика (1).doc
• Тип: Реферат; #1031549

Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»

РЕФЕРАТ

Дисциплина: Статистика

Тема: Вариация как свойство массовых явлений


Выполнила:

Ташимов Асадбек

38.03.01 «Экономика» группа:ЭН-119(2)

Проверила:

_____________________________

_____________________________

Омск 2023

Введение
Статистика изучает количественную сторону массовых общественных явлений в постоянной связи с их содержанием или количественной стороной, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени. Одной из характерных особенностей статистики является то, что при изучении количественной стороны общественных явлений и процессов она всегда отображает качественные особенности исследуемых явлений, т.е. изучает количество в неразрывной связи, единстве с качеством (качество – это свойства, присущие предмету или явлению, которые отличают данный предмет или явление от других).

Предмет статистики исследуется при помощи определённых понятий, таких как: статистическая совокупность, единица совокупности, признак, статистический показатель, система статистических показателей. Статистической совокупностью называют совокупность объектов или явлений общественной жизни, объединённых общей связью. Первичным элементом статистической совокупности, являющимся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счёта – является единица совокупности.

Общие признаки обязательно должны присутствовать среди исследуемых объектов, для того, чтобы можно было выделить статистическую совокупность или даже несколько рядов статистической совокупности для этих объектов. Совокупность объектов, имеющих один или больше общих признаков, называется однородной. А совокупность, включающая в себя разные типы и явления, является разнородной.

В принципе, любая совокупность, по отношению к разным аспектам рассматриваемых явлений, может быть однородной и разнородной одновременно. Посредством анализа содержания этих отношений, определяется возможность использования общих характеристик. Определение состава статистической совокупности, отграничение элементов разных совокупностей, достигаемое совместно с другими науками, - одна из наиболее важных задач статистики.

Одной из важнейших категорий, применяемых в статистической науке, является вариация. Явления, подверженные вариации лежат в области исследования статистической науки, в то время как явления неизменные, статичные, постоянные в статистике не рассматриваются. Вариация – это принятие единицами совокупности или их группами различных, отличающихся друг от друга, значений признака.

Вариация является результатом воздействия на единицы совокупности множества факторов. Синонимами термина «вариация» являются понятия «изменение», «изменчивость», «вариативность». Необходимость в измерении вариации возникает из-за того, что в средней величине не проявляется степень колеблемости отдельных значений признаков (вариант) вокруг среднего уровня. В зависимости от однородности в совокупности, степень колеблемости может быть большой или маленькой. Вариацией называется изменчивость только тех явлений, на которые воздействуют внешние факторы и причины. Тогда как о явлениях, изменяющихся в силу своей внутренней природы нельзя говорить, что они подвержены вариации. Например, рост человека, меняющийся в течении жизни.

Предлагаемая курсовая работа посвящена теме вариации и её показателей. В работе рассмотрены понятие, содержание и значение вариации и её показателей, раскрыты основные методики расчета и анализа показателей вариации.

Работа состоит из введения, двух разделов (теоретического и практического), заключения и списка использованной литературы и источников.

1. Вариация и ее показатели в статистике

1.1 Понятие вариации в статистике

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.

Средняя величина — это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются. В таких случаях средняя хорошо представляет всю совокупность. В других, наоборот, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность.

Колеблемость отдельных значений характеризуют показатели вариации. Термин "вариация" произошел от латинского variatio –“изменение, колеблемость, различие”. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую. Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а следовательно, насколько характерной является исчисленная средняя величина.

1.2 Вариационные ряды

В результате первой стадии статистического исследования — статистического наблюдения — получают сведения о каждой единице совокупности. Задача второй стадии статистического исследования состоит в том, чтобы упорядочить и обобщить первичный материал, свести его в группы и на этой основе дать обобщающую характеристику совокупности. Этот этап в статистике называется сводкой.

Различают простую сводку (подсчет только общих итогов) и статистическую группировку, которая сводится к расчленению совокупности на группы по существенному для единиц совокупности признаку. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства типичных явлений, обнаружить закономерности и взаимосвязи.

Результаты сводки могут быть представлены в виде статистических рядов распределения.

Статистическим рядом распределения называют упорядоченное распределение единиц совокупности на группы по изучаемому признаку. В зависимости от признака ряды могут быть вариационными (количественными) и атрибутивными (качественными).

Количественные признаки — это признаки, имеющие количественное выражение у отдельных единиц совокупности, например, заработная плата рабочих, стоимость продукции промышленных предприятий, возраст людей, урожайность отдельных участков посевной площади и т.д.

Атрибутивные признаки — это признаки, не имеющие количественной меры. Например, пол (мужской, женский), отрасль народного хозяйства, вид продукции, профессия рабочего и т.д.

Вариационные ряды могут быть дискретными или интервальными.

Дискретный ряд распределения — это ряд, в котором варианты выражены целым числом.

Интервальный ряд распределения — это ряд, в котором значения признака заданы в виде интервала.

Статистические ряды распределения позволяют систематизировать и обобщать статистический материал.

Стоит заметить, что статистические ряды распределения не дают всесторонней характеристики выделенных групп. Чтобы решить ряд конкретных задач, выявить особенности в развитии явления, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных.

Группировка - это процесс образования групп единиц совокупности однородных в каком-либо отношении, а также имеющих одинаковые или близкие значения группировочного признака.

Чтобы решить ряд конкретных задач, выявить особенности в развитии явлений, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных.

Для этой цели выбирается группировочный признак и разрабатывается система показателей, которыми будут характеризоваться выделенные группы. Определение и обоснование показателей целиком зависят от цели исследования и поставленной задачи. В зависимости от цели и задач исследования различают следующие виды группировок: типологические, структурные, аналитические.

В данной работе мы не будем подробно останавливаться на принципах группировки статистической совокупности, отметим только, что качественная сводка первичной статистической информации значительно упрощает задачу непосредственно статистического анализа, в том числе анализа на вариацию признаков.

1.3 Показатели вариации и способы их расчета

Величины признаков, характеризующих отдельные единицы статистической совокупности, изменяются под действием различных факторов. Очевидно, что чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация. Например, размер заработной платы рабочих зависит от нескольких факторов: специальности, разряда, стажа работы, образования, состояния здоровья и т.д. Чем больше различия между значениями факторов, тем больше вариация в уровне заработной платы.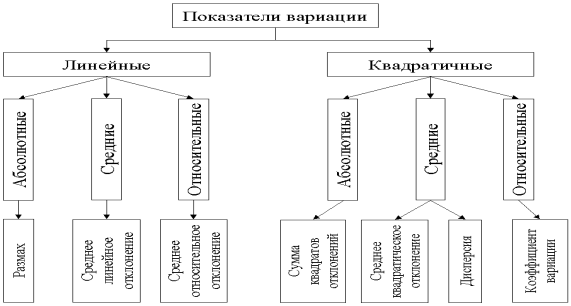


Рис. 1. Классификация показателей вариации
При характеристике колеблемости признака используют систему абсолютных и относительных показателей.

Абсолютные показатели вариации:

• 
  Размах вариации;
  
• 
  Среднее линейное отклонение
  
• 
  Дисперсия
  
• 
  Среднеквадратическое отклонение
  

Абсолютные показатели, кроме дисперсии, измеряются в тех же единицах, что и сам признак.

Относительные показатели вариации:

• 
  Коэффициент осцилляции
  
• 
  Относительное линейное отклонение
  
• 
  Коэффициент вариации
  
• 
  Относительные показатели чаще всего выражаются в процентах
  

Размах колебаний, или размах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:

Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции.

Точнее характеризует вариацию признака показатель, основанный на учете колеблемости всех значений признака. Поскольку средняя арифметическая является обобщающей характеристикой свойств совокупности, большинство показателей вариации основано на рассмотрении отклонений значений признака отдельных единиц совокупности от этой величины. К таким показателям относятся среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, представляющие собой среднюю арифметическую из отклонений индивидуальных значений признака от средней арифметической.

Среднее линейное отклонение рассчитывается из отклонений в первой степени, дисперсия и среднее квадратическое - из отклонений во второй степени. Так как алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической всегда равна нулю, то для расчета среднего линейного отклонения используется арифметическая сумма отклонений, т.е. суммируются абсолютные значения индивидуальных отклонений значений признака независимо от знака.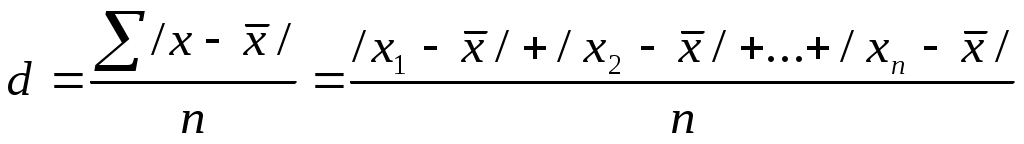

Порядок расчета среднего линейного отклонения следующий:

1) По значениям признака исчисляется средняя арифметическая:
;
2) Определяются отклонения каждой варианты от средней ;

3) Рассчитывается сумма абсолютных величин отклонений: ;

4) Сумма абсолютных величин отклонений делится на число значений: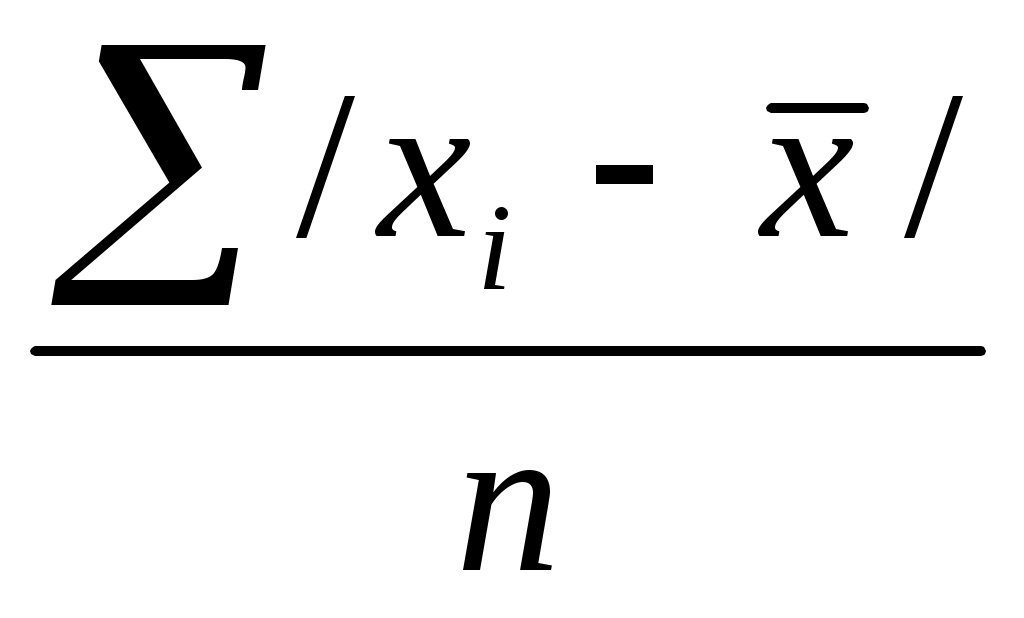
.
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:

Порядок расчета среднего линейного отклонения взвешенного следующий:

1) Вычисляется средняя арифметическая взвешенная:
;
2) Определяются абсолютные отклонения вариант от средней ;

3) Полученные отклонения умножаются на частоты ;

4) Находится сумма взвешенных отклонений без учета знака:
;
5) Сумма взвешенных отклонений делится на сумму частот:

Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.

Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается . В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
— дисперсия невзвешенная (простая);

— дисперсия взвешенная.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S: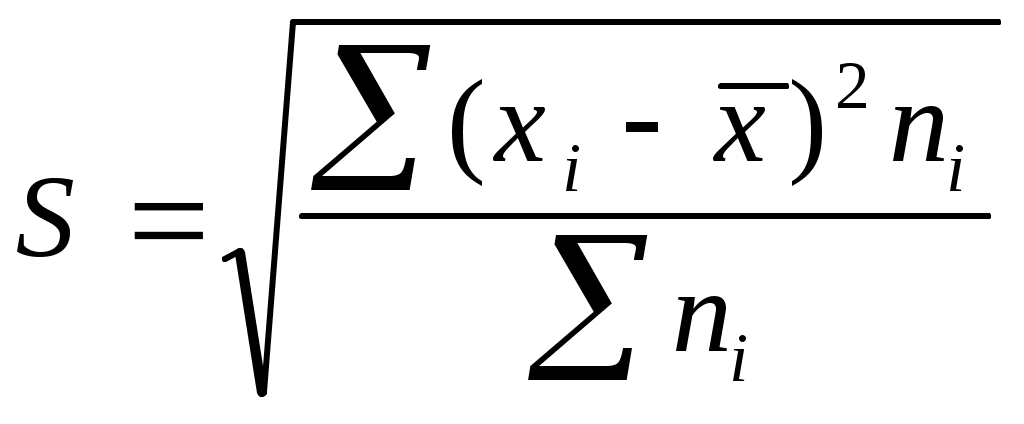
— среднее квадратическое отклонение невзвешенное;

— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.

Вычислению среднего квадратического отклонения предшествует расчет дисперсии.

Порядок расчета дисперсии взвешенной:

1) Определяют среднюю арифметическую взвешенную
;
2) Определяются отклонения вариант от средней ;

3) Возводят в квадрат отклонение каждой варианты от средней ;

4) Умножают квадраты отклонений на веса (частоты) ;

5) Суммируют полученные произведения
;
6) Полученную сумму делят на сумму весов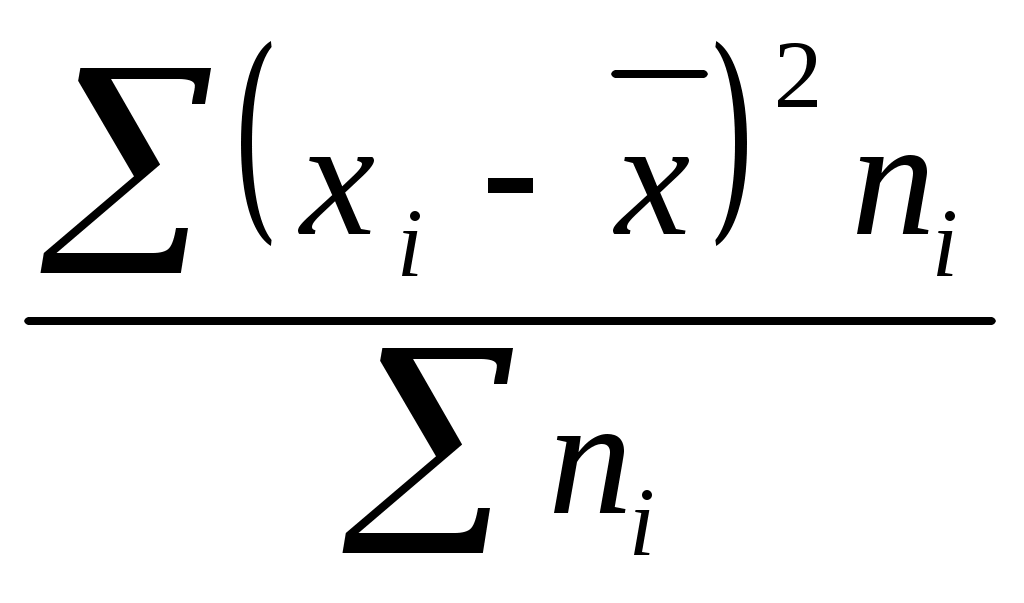
.
Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.

Свойства дисперсии:

1. 
   Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.
   
2. 
   Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.
   
3. 
   Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в раз, а среднее квадратическое отклонение - в к раз.
   
4. 
   Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: . Если А равна нулю, то приходим к следующему равенству: , т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
   

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.

Порядок расчета дисперсии простой:

1) определяют среднюю арифметическую
;
2) возводят в квадрат среднюю арифметическую
;
3) возводят в квадрат каждую варианту ряда ;

4) находим сумму квадратов вариант ;

5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат
;
6) определяют разность между средним квадратом признака и квадратом средней .

Расчет дисперсии в интервальном ряду распределения

Порядок расчета дисперсии взвешенной (по формуле ):

1. 
   определяют среднюю арифметическую
   

;

2. 
   возводят в квадрат полученную среднюю ;
   
3. 
   возводят в квадрат каждую варианту ряда ;
   
4. 
   умножают квадраты вариант на частоты ;
   
5. 
   суммируют полученные произведения ;
   
6. 
   делят полученную сумму на сумму весов и получают средний квадрат признака
   

;

7. 
   определяют разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .
   

Показатели относительного рассеивания

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах.

Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей).

Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%. вариация дисперсия

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.

3. Коэффициент вариации.

Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.

При этом исходят из того, что если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности.

1.4 Структурные характеристики вариационного ряда

Структурными характеристиками вариационных рядов являются мода и медиана.

Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.

Для интервальных рядов распределения с равными интервалами мода определяется по формуле:

где - начальное значение интервала, содержащего моду; - величина модального интервала; - частота модального интервала; - частота интервала, предшествующего модальному; - частота интервала, следующего за модальным.

Медиана - это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).

Например, стаж пяти рабочих составил 2, 4, 7, 8, 10 лет. В таком упорядоченном ряду медиана - 7 лет. По обе стороны от нее находится одинаковое число рабочих.

Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять человек в бригаде, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда:

Ме = (6 + 7) / 2 = 6,5 лет.

Медиана интервального вариационного ряда распределения определяется по формуле

где — начальное значение интервала, содержащего медиану; — величина медианного интервала; — сумма частот ряда; — сумма накопленных частот, предшествующих медианному интервалу; — частота медианного интервала.
Заключение
Вариация – это принятие единицами совокупности или их группами различных, отличающихся друг от друга, значений признака. Вариация является результатом воздействия на единицы совокупности множества факторов. Синонимами термина «вариация» являются понятия «изменение», «изменчивость», «вариативность», и в дальнейшем они будут употребляться как тождественные.

Вариация является одной из важнейших категорий, применяемых в статистической науке. Явления, подверженные вариации лежат в области исследования статистической науки, в то время как явления неизменные, статичные, постоянные в статистике не рассматриваются.Практически все явления, имеющие естественный характер происхождения, подвержены изменчивости. Например, химические процессы, синоптические явления, процессы выбора человеком спутника жизни (хотя в некоторых сообществах и этот процесс регламентируется), изменчивость наследственных признаков у каждого человека, – т.е. самые разнообразные процессы.

Искусственно созданные человеком явления, а также ряд естественных законов могут иметь неизменный характер. Например, не имеют вариативности общественные явления, регулируемые нормативными актами, закрепляющими параметры этих явлений (например, минимальный размер заработной платы, срок полномочий выборного должностного лица), или такие явления, как скорость света и притяжение Земли.

Вариацией называется изменчивость только тех явлений, на которые воздействуют внешние факторы и причины. Тогда как о явлениях, изменяющихся в силу своей внутренней природы нельзя говорить, что они подвержены вариации. Например, рост человека, меняющийся в течении жизни. Изучение изменчивости роста отдельного человека, который, допустим, к 1 году составляет 0,8 м, а к 25 годам 1,79 м, путем расчета среднего роста, будет некорректным, т.к. в начале жизни рост был небольшой в силу естественных причин.

Не следует путать с вариацией изменение размера признака у одной и той же единицы совокупности, наблюдаемой в разные периоды или моменты времени. Такое изменение называется изменением во времени или динамикой явления и исследуется с помощью специальных методов.

Необходимо подчеркнуть значение исследования вариации в статистической науке:

1. Выявление изменчивости размеров явления дает возможность оценить степень зависимости изучаемого явления от других факторов, в свою очередь подверженных изменчивости, или, другими словами, – оценить степень устойчивости явления к внешним воздействиям.

2. Вариация предполагает оценку однородности изучаемого явления, то есть меру типичности рассчитанной для этого явления средней величины.

3. Возможность оценивать вариативность определенного признака актуализирует статистические методы в условиях современной экономики, когда задачи, стоящие перед статистикой, усложняются целым рядом объективных факторов.

4. Вариация и методы ее исследования имеют важнейшее значение в изучении явлений, протекающих в обществе. Действительно, одной из главных проблем исследования общественных явлений и процессов выделяют высокий уровень их изменчивости, так как участниками общественных процессов выступают люди, обладающие различными системами ценностей и интересов.

Список литературы

1. 
   Гусаров В.М.. Теория статистики: Учеб. пособие для вузов. — М.: Аудит, ЮНИТИ, 1998.
   
2. 
   Елисеева И,И., Юзбашев М.М. Общая теория статистики: Учебник 4-е ИЗД. — М.: Финансы и статистика, 2002. — 480 с.
   
3. 
   Елисеева И.И. Моя профессия — статистик. — М.: Финансы и статистика, 1992.
   
4. 
   Елисеева И.И.. Юзбашев М.М. Общая теория статистики: Учебник / Под ред. член корр. РАН И.И. Елисеевой. 4-е изд. перераб., доп. — М.: Финансы и статистика, 2001.
   
5. 
   Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. — М.: Инфра-М, 1998.
   
6. 
   Практикум по статистике: Учеб. пособие для вузов / Под ред. В.М. Симчеры. — М.: Финстатинформ, 1999
   
7. 
   Практикум по теории статистики: Учеб. пособие / Под ред РА Шмоиловой. — М.: Финансы и статистика, 2001.
   
8. 
   Сборник задач по общей теории статистики. Учеб. пособие.__2-е изд. / Под ред. К.Э.Н., доцента Л.К. Серга. — М: Информационно-издательский дом «Филинъ», 2001.
   
9. 
   Сиденко А.В., Попов Г.Ю., Матвеева В.М. Статистика: Учебник. — М.: Дело и сервис, 2000.
   
10. 
    Статистика / Под ред. В.Г. Ионина. — Новосибирск; М., 1997.
    
11. 
    Статистика: курс лекций Л.П. Харченко, В. Ионин и др. / Под ред. В.Г. Ионина.— Новосибирск HV М, 1996
    
12. 
    Теория статистики: Учебник / Под ред. проф. Р.А. Шмойловой. 3-е изд. — М.: Финансы и статистика, 2002. — 560 с.
    
13. 
    Теория статистики: Учебник / Под ред. РЛ. II изд., перераб. — М.: Финансы и статистика, 1998.