ТРПО. Методические указания Цель работы
 Скачать 402 Kb.
|
|
Дисциплина КПО Лабораторные работы N1-5«Определение характеристик структуры ПО по её модели в виде случайного дерепва» Версия 8 Методические указания Цель работы: Рассмотреть структуру ПО, определить параметр структуры, позволяющий оценить качество структуры с точки зрения трудоёмкости отладки - числа вариантов, необходимых для отладки ПО. Создать обобщенную статистическую модель структуры ПО в виде случайного дерева, разработать соответствующую программу и показать статистическую устойчивость структурного параметра, определяющего число вариантов отладки ПО. При конструировании программы предусмотреть меры, позволяющие оценить правильность работы алгоритма программы, а затем правильность полученного результата. Эти меры должны быть встроены в код программы лабораторной работы и выводиться в отчет. 1.Теоретические основы Один из важнейших этапов разработки ПО - отладка программы может проводиться либо по методологии «черного ящика», либо по методологии «белого ящика». В первом случае внутреннее устройство ПО не известно и варианты исполнения ПО при отладке задаются путем исчерпывающих вариаций исходных данных на входе ПО, что, конечно, очень трудоемко, так как число различных сочетаний исходных данных для достаточно больших программ очень велико. Отладка ПО по методологии «белого ящика» предусматривает знание структурной схемы ПО и исполнение его при отладке по всем ветвям его структурной схемы во всем диапазоне исходных данных. При этом один из самых сильных критериев выбора вариантов исполнения ПО при отладке - все маршруты на графе ПО по управлению должны быть накрыты – проверены на правильность работы. Поэтому разработчикам ПО очень важно знать для оценок трудоемкости отладки при планировании разработки ПО число маршрутов на графе структуры ПО. Структура ПО представляется в виде графа, в вершинах (узлах) которого программные модули (программы, если это программный комплекс), а ребра характеризуют направления передач управления между программными модулями. Вспомним ряд определений и положений теории графов , необходимые нам для выполнения данной работы. Маршрут – последовательность ребер, в которой каждые 2 соседних ребра имеют общую вершину. Маршрут начинается с некоторой вершины графа и кончается на некоторой вершине. Маршрут называется цепью, если все его рёбра различны. Цепь, в которой первая и последняя вершина совпадают, называется циклом. Длиной маршрута называется число ребёр в нём. Каждое ребро считается столько раз, сколько раз встречается в маршруте. Связным графом называется любая пара вершин соединенных цепью. Связный граф без циклов называется деревом. Узлы дерева , в которые входит ребро, но ребра не выходят называются концевыми или висячими. Многие графы приложений – деревья. В каждую вершину дерева входит только одно ребро( за исключением корневого – в него не входит ни одно ребро). Можно легко убедится, что каково бы ни было дерево в нем число ребер на единицу меньше числа вершин. Эта особенность - однозначная связь между числом узлов и числом ребер отличает деревья от других графов. 2.Оценка характеристик структуры ПО Часть программных модулей ПО не имеет выходных связей с другими модулями. Они связаны с аппаратурой либо в них завершается вычислительный процесс и во внешнюю по отношению к ПО среду выдаются данные ( либо принимаются данные). То есть ПО завершает в них свою работу в соответствующих вариантах использования . Им соответствуют узлы графа, которые мы назвали «висячими». Число путей исполнения при отладке ПО должно быть равно числу висячих узлов (если граф ПО - дерево). Иными словами для деревьев искомое число вариантов исполнения ПО равно числу висячих узлов. Мы будем рассматривать графы ПО – деревья. Это конечно идеализация – часто в реальных структурах ПО в узлы могут входить несколько ребер, но и эта идеализация позволяет получить оценки многих полезных характеристик ПО, для которых точность данной идеализации достаточна. Примеры графов – деревьев приведены на рис. Висячие вершины – вершины, из которых не выходят ребра у которых нет потомков, заштрихованы. Более адекватная модель структуры ПО в виде дерева - число ребер, выходящих из каждого узла дерева не является константой, а, например, является случайным числом. Это число при построении графа может быть получено для каждого узла при помощи датчика случайных чисел. Модель случайного графа-дерева, конечно, может описывать не только структуру ПО. Распространение эпидемии, лесного пожара, финансовые пирамиды хорошо описываются данной моделью. Рассмотрим дерево, в котором всего узлов Р, а висячих узлов В. Имеет место соотношение 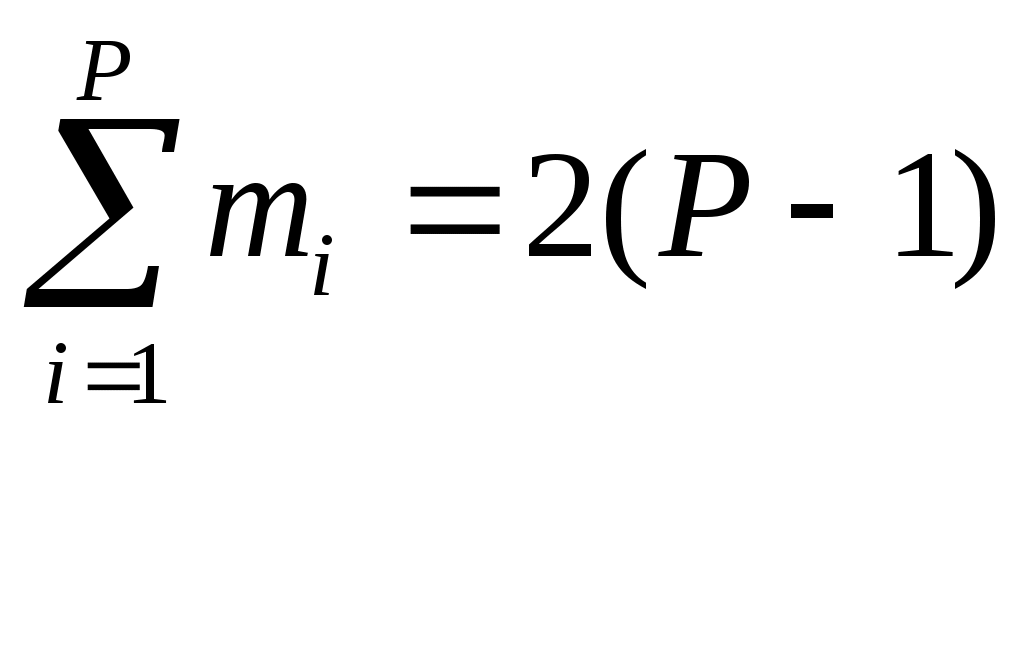 , где m i – число ребер, входящих и выходящих из i-го узла. Это соотношение легко доказывается, если вспомнить, что для дерева число ребер на единицу меньше числа узлов и при приведенном суммировании каждое ребро учитывается дважды. Для “регулярного” дерева, для которого m=const (кроме корневого и висячих узлов) эта теорема принимает вид:m – 1 + B*1 + (P – B –1)*m = 2(P – 1) После преобразований  ; ;  Для больших деревьев В достаточно велико и можно положить ( В находится в знаменателе второго члена)  Формулы получены для “регулярного дерева”, где для каждого узла (кроме корневого и висячих) m = const. В реальном ПО это не так mi const и  скорее всего величина случайная, но возможны средние оценки, которые нужно сделать для определения объема и трудозатрат при отладке даже при предположении, что mi – случайная величина. Случайный граф, в котором число ребер, исходящих из каждого узла, случайно - более адекватная модель ПО.Экспериментально можно показать, что и для случайного графа - дерева параметр  при большом дереве стремится к постоянной величине, имеющей небольшой случайный разброс и являющийся функцией m. Аналитически это доказать достаточно сложно, однако, мы в лабораторных работах покажем это численным экспериментом. 3. Правило нумерации вершин В лабораторной работе мы будем строить графы- деревья. Введем следующее удобное правило нумерации вершин графа (одно из возможных) и ведения таблиц вершин и висячих вершин: 1. Нумерация вершин сквозная десятичная от 1 до Q (Q N). При этом нумерация проводится по уровням иерархии слева направо. Корень графа имеет всегда номер 1. 2. При получении через датчик случайных чисел числа вершин -потомков им сразу же присваиваются номера (имена) и они помещаются в таблицу вершин. Таблица вершин записывается по уровням иерархии каждый уровень с новой строки. 3.В отчете в таблице вершин необходима запись вершин в одну строку с двумя разделительными пробелами между уровнями. Либо запись каждого уровня иерархии с новой строки. Число уровней иерархии подсчитывается и приводится в отчете- оно определяет высоту дерева 4. Имя вершины состоит из: порядкового десятичного номера вершины Qi N (так как N  100, то номер трехзначный).- номера узла родителя (отчества) через дефис. 5. При образовании висячей вершины ее номер помещается и в таблицу вершин и в таблицу висячих вершин. 4. Как убедиться, что написанная программа работает правильно. При работе программы вследствие неправильного алгоритма или программных ошибок могут получаться неправильные результаты. Как узнать правильный ли результат мы получили или неправильный, если мы получаем его в первый раз и использовали к тому же датчик случайных чисел? Этот вопрос составляет суть общей проблемы получения эталонных результатов при отладке. Одним из методов проверки правильности алгоритма является получение по нему на специально подобранных входных данных результата, который легко проверяется ручным подсчётом. В нашем случае это выливается в подсчёт структурного параметра α для детерминированного дерева с тем же параметром m, что и для случайного дерева, по составленному алгоритму и программе. Важно для этой проверки использовать тот же алгоритм, что и для случайного дерева. Значения α такого дерева подсчитывается в алгоритме и легко проверяется в уме по выше полученным формулам. Для построения детерминированного дерева мы заглушаем ГСЧ и он при этой проверке не работает. Нужна проверка не столько работы ГСЧ – стандартные ГСЧ работают правильно, сколько правильности работы с ГСЧ в программе работы.. Для этого надо построить гистограмму полученных в программе чисел исходящих из узла рёбер ( столбцовую диаграмму). При правильной работе с ГСЧ эта гистограмма должна быть более или менее равномерной т.е. среднее число (математическое ожидание) исходящих ребер должно не сильно отличаться от теоретического МО, равного (m-1+0) / 2. В соответствии с принципом работы ГСЧ высокая равномерность результатов достигается только при очень большом числе реализаций. Пример гистограммы для m = 4 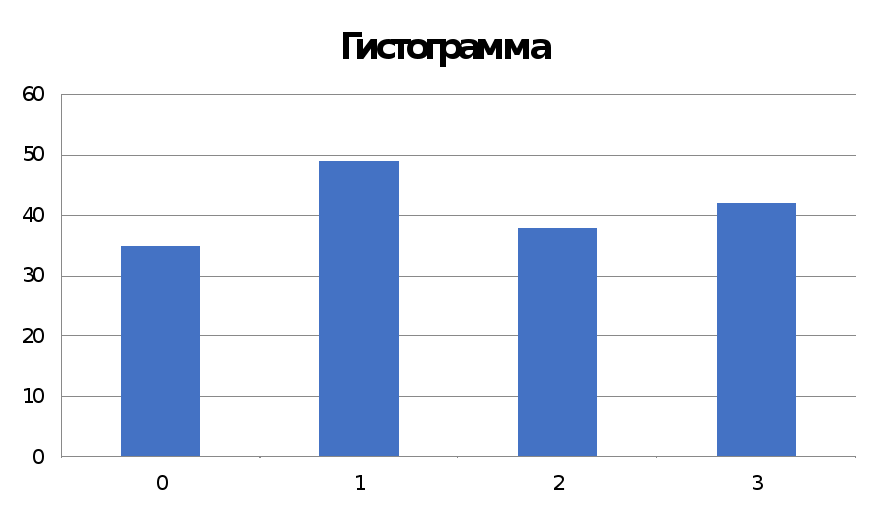 Е График зависимости значений от числа вершин в графе 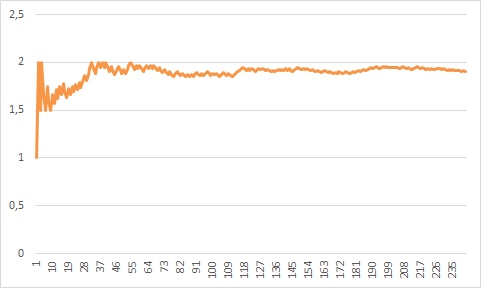 И наконец, необходимо использовать «утверждения» для встроенного контроля работы программы. Утверждения это не словесный оборот или языковая категория это конструкция языка программирования (логическое условие), предназначенная для обнаружения ошибок (assert). Для образования утверждения в нашем случае необходимо использовать тот факт, что α случайного дерева всегда больше α детерминированного дерева, так как случайное дерево всегда более узкое, чем детерминированное и если получилось так. что для случайного дерева α = < (m-1) /( m-2), то в программе имеется ошибка. Рассмотрим пример случайного дерева и нумерации узлов. . 1-0 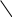     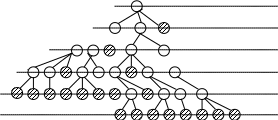2-1 4-1 3-1 9-3 8-3 5-2 7-2 6-2 5.Алгоритм образования случайного графа-дерева 1.Граф рассматривается по уровням (послойно). На первом уровне всегда одна вершина (узел). 2.Число вершин (узлов) на втором уровне и всех последующих определяется числом ребер, исходящих и входящих в / из узлов-родителей. Число этих ребер назначается при помощи датчика случайных чисел. Случайное число должно быть распределено равномерно в диапазоне 0 …m-1. 3. Настройки датчика случайных чисел производятся исходя из минимального числа ребер, исходящих из каждой вершины (узла) – 0, максимального – (m – 1). Для расчета случайного графа число m – задается в исходных данных. Например, если m – 1 = 3 (m=4), то диапазон случайных значений числа выходящих из узла ребер либо 0, либо 1, либо 2, либо 3. 4. Вершины (узлы) каждого уровня помещаются в свою строку «таблицы вершин». По каждой строке таблицы проводится подсчет количества вершин. 5. Висячие узлы помещаются в таблицу висячих вершин. Они также присутствуют в таблице всех вершин. 6. Производится подсчет числа путей на графе. Это число характеризует, трудоемкость отладки ПО. Для дерева – это число висячих вершин. Примечание. Наличие циклов графа и дополнительных связей между узлами влияет на число путей, но не влияет на параметр . Таким образом, полученная оценка даёт нижнюю границу числа вариантов на отладку ПО Подсчитывается также число уровней иерархии графа – высота дерева. Производится подсчет параметра Число всех вершин = ----------------------------- . Число висячих вершин Данное число является случайным, так как получено с помощью датчика случайных чисел. Расчет графа и строкообразование таблицы не может продолжаться бесконечно. Этот процесс останавливается в соответствии с исходными данными, в которых задано правило остановки. 6.Правила остановки Правила остановки вычислений для построения графа. В работе применено два правила остановки вычислений для построения графа: правило А и правило В. Правило А – построение графа прекращается при достижении числа узлов заданного значения N. Правило В-построение графа прекращается при выполнении двух условий. Первое условие - число узлов заданному числу N. Второе условие- последний уровень иерархии графа должен быть до конца заполнен висячими узлами иными словами во всех узлах предыдущего уровня процесс генерации узлов должен быть проведен. Для этого в алгоритме построения графа с правилом остановки В необходимо запоминать имя последнего узла каждого уровня после чего проверять первое условие. Иными словами по правилу В расчет графаведется до тех пор, пока сумма числа узлов Q по всем завершенным строкам( уровням иерархии графа) не станет заданного числа . Как только сумма числа узлов по таблице достигнет числа заданного в правиле остановки, расчет прекращается, и все узлы последней строки объявляются висячими. Для правила остановки А к висячим узлам надо добавить и узлы предпоследнего уровня, не успевшие дать потомков из-за остановки вычислений К этому числу висячих узлов добавляются все висячие узлы на предыдущих уровнях, не имеющие потомков, – узлы, у которых число исходящих ребер получилось равным 0. 7.Статистические исследования 1. Расчет построения повторяется для другого случайного графа, который образуется по описанному алгоритму (в цикле) при других значениях случайного числа ребер исходящих из узлов графа, но при тех же исходных данных m и N Число построенных случайных графов R задается в исходных данных к заданию 2. Если при первом шаге для верхней вершины (корневой) датчик случайных чисел показывает 0 потомков ( такое вполне может быть), то расчет графа прекращается и делается следующая попытка. Это справедливо только для первого шага. Этот случай в отчете и при подсчете R не учитывается. 3. Если граф обрывается ( такое вполне может быть при небольших значениях m в частности при m=3) при числе построенных узлов меньше 10 , то эта реализация также в отчет и счетчик R не берется см. п8. 10. В результате построения R случайных деревьев получается R случайных значений параметра . Необходимо вычислить математическое ожидание этого параметра и привести его в отчете. 8.Содержание работ N 1-5 и представление результатов Работа 1.Анализ предметной области, синтез модели структуры программы (схема программы). Работа 2. Построить случайный граф ПО, для которого число выходящих из вершины ребер определяется датчиком случайных чисел. Определить значение структурного параметра   всех узлов /число висячих узлов. В отчет помещаются таблица вершин, таблица висячих вершин и гистограмма полученных случайных значений числа исходящих из узлов ребер ( максимальное значение m-1 ) для одного из вариантов случайного графа того же , что и по п.2. Привести гистограмму для полученных при построении графа значений (m-1). Убедится в правильности построения гистограммы. В тексте программы и в отчете привести «утверждение», подтверждающее правильность гистограммы. Правило остановки построения графа (А или В) приведено в задании. Внимание. В гистограмме приводится число нулей, полученных только от датчика случайных чисел, а не в результате применения правила остановки, так как гистограммой проверяется правильность работы с датчиком случайных чисел Работа 3. Этим же алгоритмом построить детерминированный граф ПО при фиксированном значении числа выходящих из узлов ребер (mфикс -1) = (m-1). Это можно сделать, заглушая обращение к датчику случайных чисел, и для каждого узла использовать заданную константу при определении числа исходящих ребер. Определить число висячих узлов и параметр . Убедится в правильности расчета структурного параметра α. В тексте программы и в отчете привести «утверждение» относительно α случайного дерева.Работа 4. Подсчитать среднее число висячих вершин у совокупности R случайных графов ПО, определить среднее значение и дисперсию структурного параметра = отношению общего числа вершин к числу висячих вершин. Работа 5. Исследовать сходимость значения структурного параметра к устойчивому значению с ростом числа узлов графа Р, построив для этого функцию изменения структурного параметра с ростом числа узлов Р. Для данного графа построить графический фрагмент из первых двадцати узлов. Этот фрагмент помогает построить начало графика (Р).По завершению цикла лабораторных работ должен быть подготовлен, и предъявлен на проверку преподавателю отчет. Принятый преподавателем отчет сохраняется и предъявляется на экзамене. Без проведенных лабораторных работ и наличия отчета студент на экзамен не допускается . Перечень заданий. Варианты заданий Для заданий № ХХ-А правило остановки А. Для заданий № XX –B правило остановки В. Задание № 1: m =4, N = 200, R = 100 А, В Задание № 2: m =4, N = 200, R = 400 А, В Задание № 3: m =3, N = 200, R = 100 А,В Задание № 4: m =3, N = 200, R =400 А,В Задание № 5: m =5, N = 200, R = 100 А, В Задание № 6: m =5, N = 200, R = 400 А, В Задание № 7: m =6, N = 200, R = 100 А, В Задание № 8: m =6, N = 200, R = 400 А, В Задание № 9: m =4, N = 100, R = 400 А, В Задание №10: m =4, N = 100, R = 100 А, В Задание № 11: m =3, N = 100, R = 400 А,В Задание № 12: m =3, N = 100, R = 100 А,В Задание №13: m =5, N = 100, R = 100 А, В Задание № 14: m =5, N = 150, R = 400 А, В Задание № 15: m =6, N = 200, R = 100 А, В Задание № 16: m =6, N = 150, R = 400 А, В Задание № 17: m =3, N = 50, R = 200 А,В Задание №18: m =4, N = 50, R = 200 А, В Задание № 19: m =6, N = 50, R =200 А, В Задание №20: m =5, N = 50, R = 200 А, В Литература 1. Мостовой Я.А. Лекции по технологии разработки программного обеспечения. Учебное пособие. Самара. Изд ПГУТИ.ISBN 978-5-904029-45-6, 2014. – 178с. |