ТРПО. Методические указания Цель работы
 Скачать 402 Kb.
|
|
Контроль отлаженности (надёжности) ПО в процессе отладки. Гипотеза Джелинского – Моранды и математическая модель надежности ПО Лабораторные работы №6 - 9 Версия 8 Цель работы : Определение параметров модели надежности ПО. Прогнозирование числа оставшихся ошибок ПО при отладке и эксплуатации. В результате выполнения данных лабораторных работ студент получает навык: 1) определения момента достижения ПО требуемой надежности в процессе отладки, 2) использования метода наименьших квадратов для обработки данных, Введение Крайне желательно иметь модель прогнозирования надежности ПО, по которой можно было оценивать, например, необходимость продолжения отладки, планировать точку останова этого процесса. На пути создания такой достаточно общей и универсальной модели казалось бы имеются два препятствия: -ПО чрезвычайно разнообразно по назначению и сложности, - ПО разрабатывается различными людьми, частота ошибок у них отличается во много раз. Однако, эти препятствия преодолеваются, если допустить наличие в модели надежности свободных параметров, которые для конкретного ПО, разработанного конкретными людьми, могут быть определены по наблюдениям за проявлением ошибок при работе этого ПО на определенном интервале времени. При этом число свободных параметров модели желательно иметь небольшим, а число экспериментальных данных наоборот большим. При этом опасаться того, что число переменных может стать меньше числа уравнений для их определения, не надо. Метод наименьших квадратов (МНК), которым мы будем пользоваться, не только фильтрует случайные ошибки экспериментальных данных, но и позволяет получать решение переопределенной в алгебраическом смысле системы уравнений. 1.Модель Джелинского – Моранды Ошибки в ПО имеют скрытый характер и проявляются только при определенных наборах входных данных. Те грубые ошибки в ПО, которые проявляются сразу при любых исходных данных, сразу же и устраняются. Математическая модель проявления ошибок в ПО Джелинского – Моранды имеет понятный физический смысл: чем больше ошибок в ПО, тем чаще они проявляются при работе. По мере возрастания отлаженности ПО, уменьшается количество оставшихся в нем ошибок и частота их проявления также падает.  Математическая формулировка гипотезы Джелинского – Моранды: интенсивность (скорость) проявления ошибок в ПО пропорциональна числу оставшихся ошибок. dn/dt =K×(N0 – n) или обозначая среднюю интенсивность проявления ошибок = К  (No-n).Здесь N0 – начальное число ошибок , n –число обнаруженных ошибок, К – коэффициент пропорциональности Рассмотренная модель изменения надежности ПО Джелинского - Моранды позволяет, основываясь на наблюдениях за процессом проявления ошибок в ПО, определить характеристику надежности ПО – интенсивность проявления ошибок , а точнее параметры модели : начальное количество ошибок N0 и параметр К , определяющий скорость проявления ошибок. Конечно же никакая модель не может предсказать конкретное место и содержание ошибки, но это и не надо для поставленных целей. Решение упомянутого выше дифференциального уравнения первого порядка относительно числа проявившихся ошибок n n = N0 ( 1 – е-кt ) и  N0 е-кt К>0При экспериментальных наблюдениях за проявлением ошибок в ПО удобнее не рассматривать общее количество проявившихся ошибок с нарастающим итогом, а рассматривать количество ошибок, проявившихся на фиксированных интервалах времени. Запишем выражение для количества ошибок, проявившихся на интервале ti, полагая равномерным шаг наблюдений за проявлениями ошибок t. 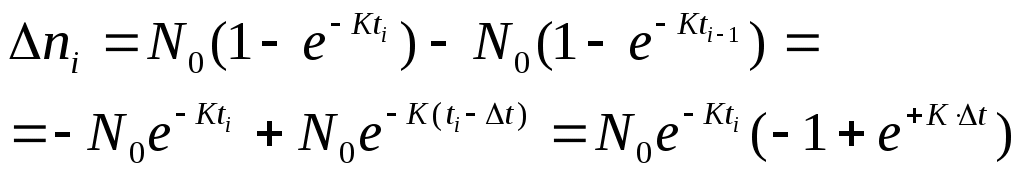 Здесь ni - приращение количества обнаруженных ошибок на интервале t. Пусть шаг t можно выбрать так, чтобы произведение Кt 1. Тогда, разлагая exp функцию в ряд и пренебрегая членами выше 1-ой степени Кt, как малыми, имеем : еxp(x)=1+х/1!+ х 2 /2!+…..  В данном уравнении два неизвестных N0 и К. Для их определения достаточно рассмотреть два различных интервала t - будет два уравнения с двумя неизвестными. Однако, возникает вопрос какую пару интервалов из r >2 имеющихся интервалов наблюдений выбрать для определения N0 и К, так как каждой паре интервалов соответствует в общем случае свое решение относительно N0 и К. Полученное по каждой паре случайно «пляшущих» данных решение не соответствует всей совокупности экспериментальных данных и в этом смысле нас не устраивает. Таким образом, подход, связанный с выбором 2 наблюдений, приводит к неправильному результату. Нужно использовать всю совокупность наблюдений. Однако, это на первый взгляд приведет к получению переопределенной системы уравнений (число уравнений из которых можно определить значения N0 и К, больше числа неизвестных -2). Как же получить значения двух неизвестных параметров модели N0 и К, используя всю совокупность исходных данных? 2.Метод наименьших квадратов для аппроксимации экспериментальных данных Получим решение, удовлетворяющее в некотором смысле всей совокупности экспериментальных данных. При этом не будем стремиться, чтобы решение удовлетворяло точно всем экспериментальным точкам (к тому же в рамках рассмотренной простой модели всего с двумя свободными параметрами это невозможно по алгебраическим соображениям). Значение неизвестных параметров N0 и К будем определять, исходя из минимизации суммы квадратов невязок между экспериментальными данными ni и значениями ni , определяемыми по модели (1). Этот метод называется методом наименьших квадратов. Он позволяет разрешить в алгебраическом смысле переопределенную систему, когда число наблюдений превышает число переменных. В результате использования метода наименьших квадратов получается «решение», удовлетворяющее всем наблюденным значениям в смысле минимизации суммы квадратов отклонений решения от наблюденных значений. 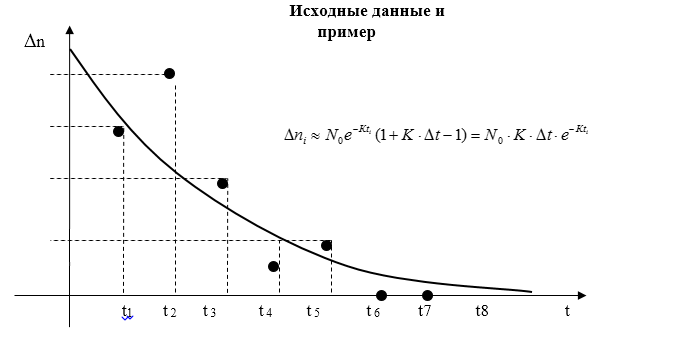 Введем понятие невязки, как разницы между экспериментальным значением переменной для какого-то значения аргумента и значением переменной по рассматриваемой теоретической модели для того же значения аргумента. Δi= Δni – N0×Δt×K×e-Kti Запишем сумму квадратов невязок  Найдем значение N0 и К, при которых эта сумма имеет минимум. Для этого найдем производные суммы квадратов невязок по искомым параметрам и приравняем их 0. 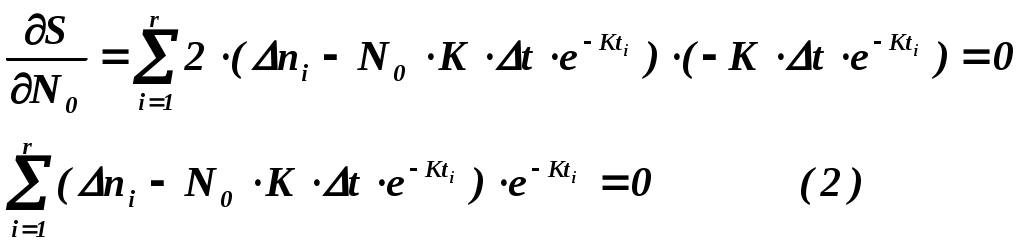 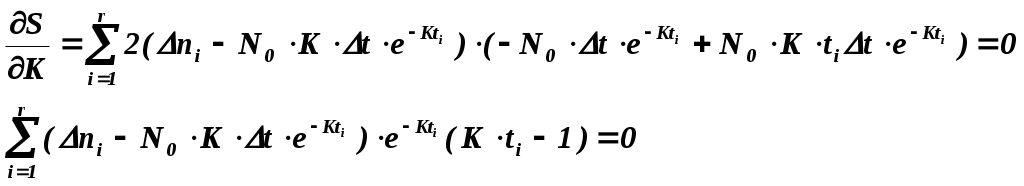 Отсюда следует, что  Но из (2) следует, что первое слагаемое равно 0. Окончательно получим уравнение, которое совместно с (2) образует систему 2-х уравнений с двумя неизвестными N0 и К. 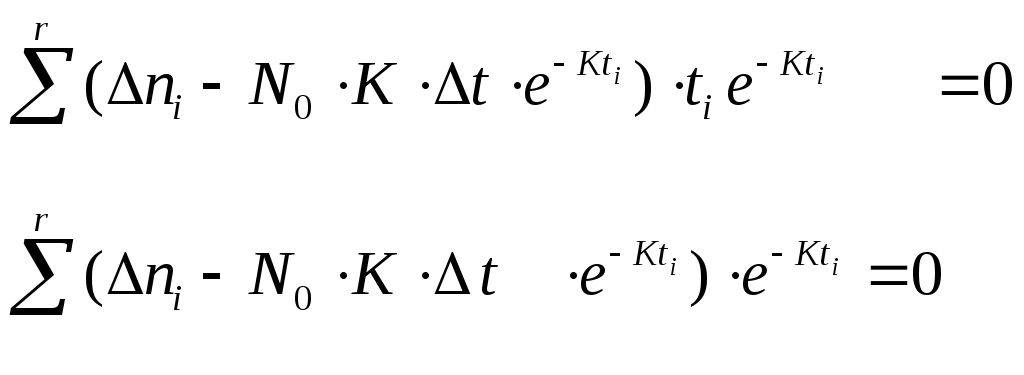 Выразим из 1-го уравнения N0, суммируя по частям и вынося постоянные, не зависящие от индекса i, за знак суммы 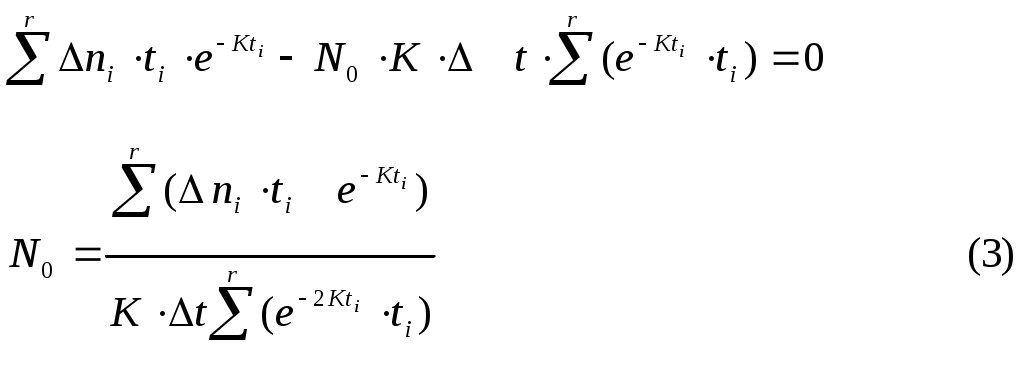 Подставляя это выражение во второе уравнение, имеем О 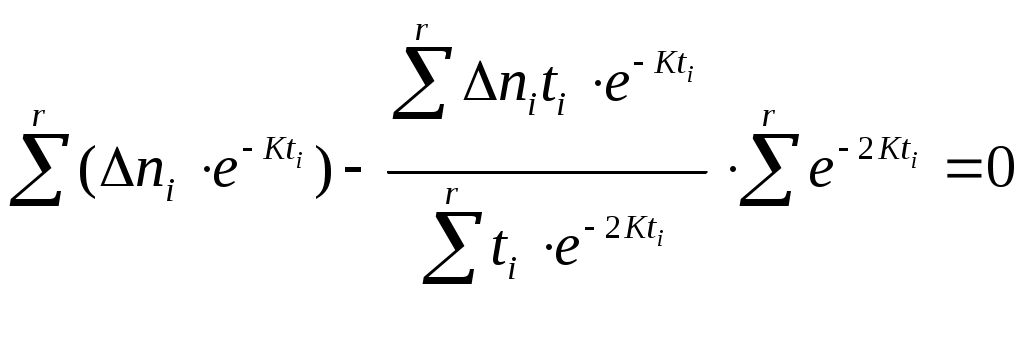 тсюда 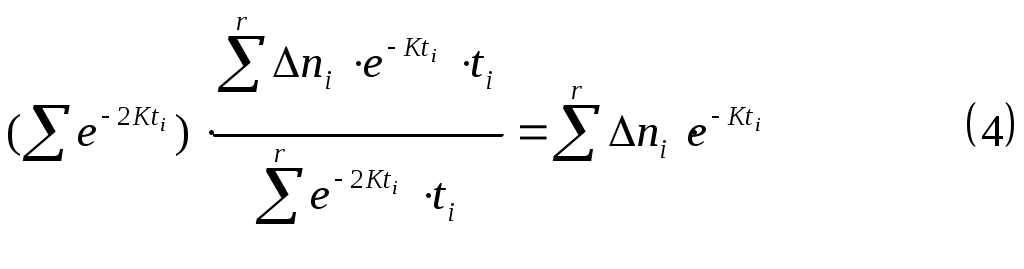 3.Метод решения трансцендентного уравнения (4) Из данного трансцендентного уравнения относительно только одного неизвестного К численным методом можно определить К. Суть метода – организация итерационной процедуры вычисления левой и правой части равенства при различных значениях К. Сначала зададимся нулевым приближением параметра К и вычислим левую и правую часть уравнения (4). Они наверняка не совпадут. Это означает, что нулевое приближение не является корнем данного уравнения. Возьмем другое значение  К, отличающееся на  К. Если мы удачно выбрали знак К , то значения левой и правой части уравнения 4 сблизятся. Далее, изменяя К добъемся того, чтобы левая и правая часть равенства были бы равны друг другу с очень малой погрешностью, например, 0,0001. Это значение К и примем за корень уравнения(4).Подставляя определенное значение К в (3), можно определить N0. В разделе 7 приведен пример итерационной процедуры определения К. 4. Оценка момента завершения отладки по наблюдению за процессом проведения ошибок Отладка ПО должна проводиться по плану и завершаться по выполнению намеченного плана. Вопросы выбора критериев отлаженности ПО и составления плана отладки в соответствии с этими критериями отдельно рассматриваются в соответствующих курсах. Модель Джелинского - Моранды может независимо и достаточно достоверно оценивать ход процесса отладки, который целесообразно прекращать, когда все ошибки обнаружены и интенсивность их проявления стала очень низка. Однако, имеются два вопроса, которые надо снять для того, чтобы получить ответ на вопрос когда можно прекращать отладку? Во первых, модель непрерывная и может показывать дробное число ошибок на заданный момент времени, в том числе и значение количества оставшихся ошибок меньше 1. Конечно, это не соответствует физическому смыслу и может считаться недостатком модели. Во вторых, модель никогда не покажет точный нуль. Количество оставшихся ошибок будет приближаться к нему по экспоненте бесконечно долго. Однако, построение дискретной модели, показывающей только целое число ошибок, гораздо более сложно и рассматривать её мы не будем . Результат рассмотрения дискретной модели совместно с данной непрерывной показывает, что вероятности отсутствия ошибок в ПО равная 0,999 ( это высокая надежность ПО) соответствует значение «0.0001 ошибки» в данной непрерывной модели см приложение. Достижение количества оставшихся ошибок значения 0.0001 мы и будем принимать как сигнал достижения требуемой надежности ПО и прекращения отладки. Следует подчеркнуть, что в реальных ситуациях отладки ПО она считается завершенной по исчерпанию программы отладки, составленной исходя из выбранных критериев, например, накрытию всех путей на графе ПО. Определение достаточности проведенной отладки по модели Джелинского-Моранды является дополнительным методом, подтверждающим достигнутую надежность ПО – малую интенсивность проявления ошибок ПО. 5.Содержание работ и требования к оформлению. Работа №6. Анализ предметной области и экспериментальных данных по заданию. Привести расчетные формулы и кратко суть метода наименьших квадратов.Привести исходные данные. Работа N7. Составление программы для определения с помощью МНК параметров No и К модели надежности ПО Джелинского-Моранды по заданным данным как бы «случайного» изменения во времени числа обнаруженных ошибок Эти данные приводятся в индивидуальном задании к работе. Определить параметры модели No и К численной процедурой. Привести расчет параметров модели Джелинского-Моранды проявления ошибок в ПО К и N0. Привести таблицу с окончательным и промежуточными результатами численного метода определения К. Ошибка сходимости при определении К  Построить график изменения числа обнаруженных ошибок во времени по модели надежности ПО Джелинского – Моранды с определенными N0 и К с прогнозом до t  10.Нанести на этот график точки наблюдений из исходных данных. Привести значение суммы квадратов невязок. График строить, начиная со значения t=0. Сделать проверку для этого случая Построить значения невязок и квадратов невязок для количества проявившихся ошибок и нанести их на график по точкам исходных данных. Работа N8 Составление программы определения с помощью МНК параметров линейной аппроксимации изменений случайного числа обнаруженных ошибок по данным лабораторной работы №7. Сравнение результатов работ №7 и №8 , выводы. Построить график прогнозируемого числа ошибок с линейной аппроксимацией МНК и экстраполяцией за интервал наблюдения до t=10. по тем же исходным данным, что в работе 5. Использовать линейную интерполяцию МНК по уравнению у=а+вt, где а и в неизвестные параметры, подлежащие определению по экспериментальным данным. График строить, начиная со значения t=0. Сделать проверку для этого случая. Нанести на график точки из исходных данных. Привести полученные значения коэффициентов a и в аппроксимирующей прямой и выражения для их получения. Построить значения невязок и квадратов невязок и нанести их на график. Привести значение суммы квадратов невязок Сделать заключение по возможности прогноза числа оставшихся ошибок и по качеству аппроксимации исходных данных. Работа№9 Определить прогнозируемое время завершения отладки по анализу экспериментальных данных по модели Джелинского - Моранды. 6   t1 t 2 t 3 t 4 t 5 t 6 t7 t8 t n         4  3 2 1 Исходные данные .ЗАДАНИЯ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||