Вариант 13 Задание 1 (Ресурсная задача)
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
Вариант 13 Задание 1 (Ресурсная задача) Для изготовления изделий типа А и В используется сырье трех видов, запасы каждого из которых Р 1 =648, Р 2 = 352, Р 3 = 208. На производство одного изделия типа А требуется затратить а 1 =3 кг сырья первого вида, а2 =4 кг сырья второго вида, а 3 =2 кг сырья третьего вида. На одно изделие типа В расходуется соответственно b 1= 9 b2 =2 b3=2 кг сырья каждого вида. Прибыль от реализации единицы изделия А составляет a =4 /ден.ед./, а изделия В - b =3 /ден.ед./. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплекс-методом. Дать геометрическое истолкование задачи. Решение симплекс-метод прибыль изделие Определим максимальное значение целевой функции F(X) = 4x1 + 3x2 при следующих условиях-ограничений. 3x1 + 9x2≤648 4x1 + 2x2≤352 2x1 + 2x2≤208 В 1-м неравенстве смысла вводим базисную переменную x3. В 2-м неравенстве смысла вводим базисную переменную x4. В 3-м неравенстве смысла вводим базисную переменную x5. 3x1 + 9x2 + 1x3 + 0x4 + 0x5 = 648 4x1 + 2x2 + 0x3 + 1x4 + 0x5 = 352 2x1 + 2x2 + 0x3 + 0x4 + 1x5 = 208 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: Решим систему уравнений относительно базисных переменных: x3, x4, x5, Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,648,352,208) Базисное решение называется допустимым, если оно неотрицательно.
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (648 : 3 , 352 : 4 , 208 : 2 ) = 88 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (4) и находится на пересечении ведущего столбца и ведущей строки.
Вместо переменной x4 в план 1 войдет переменная x1. Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x4 плана 0 на разрешающий элемент РЭ=4 Таким образом, в новом плане 1 заполнены строка x1 и столбец x1. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (4), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (384 : 71/2 , 88 : 1/2 , 32 : 1 ) = 32 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (1) и находится на пересечении ведущего столбца и ведущей строки.
Вместо переменной x5 в план 2 войдет переменная x2. Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x5 плана 1 на разрешающий элемент РЭ=1 На месте разрешающего элемента в плане 2 получаем 1. В остальных клетках столбца x2 плана 2 записываем нули. Таким образом, в новом плане 2 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 72 x2 = 32 F(X) = 4•72 + 3•32 = 384 Область допустимых решений представляет собой многоугольник Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых(2) и (3), то ее координаты удовлетворяют уравнениям этих прямых: 4x1+2x2=352 2x1+2x2=208 Решив систему уравнений, получим: x1 = 72, x2 = 32 Откуда найдем максимальное значение целевой функции: F(X) = 4*72 + 3*32 = 384 Задание 2. (Транспортная задача) Имеются 3 пункта поставки однородного груза А 1 , А 2 , А 3 и 5 пунктов потребления этого груза В 1 , В 2 , В 3 , В 4 , В 5 . На пунктах А I ( I = 1,2,3 ) груз находится соответственно в количествах а 1 , а 2 , а 3 условных единиц. В пункты В J (J=1,2,3,4,5) требуется доставить соответственно b J единиц груза. Стоимость перевозки единицы груза (с учетом расстояний) из А I в В J определена матрицей С={c ij}. Решить задачу тремя методами (северо-западного угла, минимальной стоимости и методом Фогеля) и найти такой план закрепления потребителей и поставщиков, чтобы общие затраты на перевозки были минимальны. а 1 =150, а 2 = 230, а 3 = 250, b 1 =110, b 2 =100, b 3 = 200, b 4 = 140, b 5 = 80, 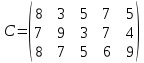 Решение 1. Метод северо-западного угла
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 150 + 230 + 250 = 630 ∑b = 110 + 100 + 200 + 140 + 80 = 630 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. x11 = min (150,110) = 110 x12 = min (40,100) = 40. x22 = min (230,60) = 60. x23 = min (170,200) = 170. x33 = min (250,30) = 30. x34 = min (220,140) = 140. x35 = 80.
число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным. Стоимость перевозок по этому плану: Z1 = 8*110 + 3*40 + 9*60 + 3*170 + 5*30 + 6*140 + 9*80 = 3760 Проверим оптимальность опорного плана, полагая, что u1 = 0. u1 + v1 = 8; 0 + v1 = 8; v1 = 8 u1 + v2 = 3; 0 + v2 = 3; v2 = 3 u2 + v2 = 9; 3 + u2 = 9; u2 = 6 u2 + v3 = 3; 6 + v3 = 3; v3 = -3 u3 + v3 = 5; -3 + u3 = 5; u3 = 8 u3 + v4 = 6; 8 + v4 = 6; v4 = -2 u3 + v5 = 9; 8 + v5 = 9; v5 = 1 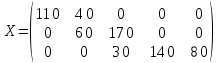 Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vi > cij (2;1): 6 + 8 > 7; ∆21 = 6 + 8 - 7 = 7 (2;5): 6 + 1 > 4; ∆25 = 6 + 1 - 4 = 3 (3;1): 8 + 8 > 8; ∆31 = 8 + 8 - 8 = 8 (3;2): 8 + 3 > 7; ∆32 = 8 + 3 - 7 = 4 max (7,3,8,4) = 8 Перспективная клетка (3;1). Сдвиг цикла 30. В результате получим новый опорный план. 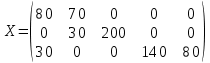 Проверим оптимальность опорного плана. u1 + v1 = 8; 0 + v1 = 8; v1 = 8 u3 + v1 = 8; 8 + u3 = 8; u3 = 0 u3 + v4 = 6; 0 + v4 = 6; v4 = 6 u3 + v5 = 9; 0 + v5 = 9; v5 = 9 u1 + v2 = 3; 0 + v2 = 3; v2 = 3 u2 + v2 = 9; 3 + u2 = 9; u2 = 6 u2 + v3 = 3; 6 + v3 = 3; v3 = -3 Опорный план не является оптимальным, так как: (1;5): 0 + 9 > 5; ∆15 = 0 + 9 - 5 = 4 (2;1): 6 + 8 > 7; ∆21 = 6 + 8 - 7 = 7 (2;4): 6 + 6 > 7; ∆24 = 6 + 6 - 7 = 5 (2;5): 6 + 9 > 4; ∆25 = 6 + 9 - 4 = 11 max (4,7,5,11) = 11 Перспективная клетка (2;5). Сдвиг цикла 30 В результате получим новый опорный план. 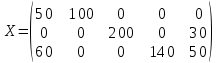 Проверим оптимальность опорного плана u1 + v1 = 8; 0 + v1 = 8; v1 = 8 u3 + v1 = 8; 8 + u3 = 8; u3 = 0 u3 + v4 = 6; 0 + v4 = 6; v4 = 6 u3 + v5 = 9; 0 + v5 = 9; v5 = 9 u2 + v5 = 4; 9 + u2 = 4; u2 = -5 u2 + v3 = 3; -5 + v3 = 3; v3 = 8 u1 + v2 = 3; 0 + v2 = 3; v2 = 3 Опорный план не является оптимальным, так как (1;3): 0 + 8 > 5; ∆13 = 0 + 8 - 5 = 3 (1;5): 0 + 9 > 5; ∆15 = 0 + 9 - 5 = 4 (3;3): 0 + 8 > 5; ∆33 = 0 + 8 - 5 = 3 max (3,4,3) = 4 Перспективная клетка (1;5). Сдвиг цикла 50 В результате получим новый опорный план. 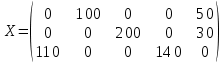 u1 + v2 = 3; 0 + v2 = 3; v2 = 3 u1 + v5 = 5; 0 + v5 = 5; v5 = 5 u2 + v5 = 4; 5 + u2 = 4; u2 = -1 u2 + v3 = 3; -1 + v3 = 3; v3 = 4 u3 + v5 = 9; 5 + u3 = 9; u3 = 4 u3 + v1 = 8; 4 + v1 = 8; v1 = 4 u3 + v4 = 6; 4 + v4 = 6; v4 = 2 Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vi <= cij. Минимальные затраты составят: Zmin = 3*100 + 5*50 + 3*200 + 4*30 + 8*110 + 6*140 = 2990 2. Метод Фогеля Получим таблицу:
Стоимость перевозок по этому плану: Z1=100*3+50*5+200*3+30*4+110*8+140*6=300+250+600+120+880+840=2990 Проверим оптимальность опорного плана. u1 + v1 = 8; 0 + v1 = 8; v1 = 8 u3 + v1 = 8; 8 + u3 = 8; u3 = 0 u3 + v4 = 6; 0 + v4 = 6; v4 = 6 u1 + v2 = 3; 0 + v2 = 3; v2 = 3 u1 + v5 = 5; 0 + v5 = 5; v5 = 5 u2 + v5 = 4; 5 + u2 = 4; u2 = -1 u2 + v3 = 3; -1 + v3 = 3; v3 = 4 Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vi <= cij. Минимальные затраты составят: Z min = 2990 3. Метод минимальной стоимости Минимальный тариф c12=3, x12 = min (150,100) = 100. c23=3, x23 = min (230,200) = 200. c25=4, x25 = min (30,80) = 30. c15=5, x15 = min (50,50) = 50. c34=6, x34 = min (250,140) = 140. x31 = min (110,110) = 110.
Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 7. Следовательно, опорный план является вырожденным. Значение целевой функции для этого опорного плана равно: Z1 = 3*100 + 5*50 + 3*200 + 4*30 + 8*110 + 6*140 = 2990 Следовательно, заполняем числом «0» пустую клетку (3,3), т.к. она имеет минимальный тариф (с33 = 5), и не образует с занятыми клетками замкнутого прямоугольного контура. Получаем опорный план:
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vi <= cij. Минимальные затраты составят: Zmin = 3*100 + 5*50 + 3*200 + 4*30 + 8*110 + 6*140 = 2990 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
