Главная страница
Навигация по странице:

  • Найдем необходимые числовые характеристики

  • Значимость коэффициента корреляции

    		•

    4510321_Статистика. Вариант 2 Задача 1


    Скачать 80.9 Kb.
    НазваниеВариант 2 Задача 1
    Дата07.06.2020
    Размер80.9 Kb.
    Формат файлаdocx
    Имя файла4510321_Статистика.docx
    ТипЗадача
    #128691
    страница3 из 3
    1   2   3

    Задача 5.


    В таблице приведено распределение 120 коров по дневному надою ξ (в кг) и жирности молока η(в %):

    ξ

    η
    Менее 7
    7-10
    10-13
    13-16
    Более 16
    Итого

    Мене 3,2









    8



    8

    3,2-3,6






    2
    16
    8
    26

    3,6-4,0



    4
    16
    10
    2
    32

    4,0-4,4
    2
    6
    10
    2



    20

    Более 4,4
    8
    6
    20






    34

    Итого
    10
    16
    48
    36
    10
    120


    1) Вычислить групповые средние 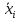и и 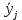построить эмпирические линии регрессии;

    2) Предполагая, что между переменными ξ и η существует линейная корреляционная зависимость:

    а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать содержательную интерпретацию полученных уравнений;

    б) вычислить коэффициент корреляции, на уровне значимости а = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными ξ и η;

    в) используя соответствующее уравнение регрессии, оценить средний процент жирности молока для коров, дневной удой которых составляет 15 кг.
    Перейдем к серединам интервалов

     
    5,5
    8,5
    11,5
    14,5
    17,5
    Итого

    3
    0
    0
    0
    8
    0
    8

    3,4
    0
    0
    2
    16
    8
    26

    3,8
    0
    4
    16
    10
    2
    32

    4,2
    2
    6
    10
    2
    0
    20

    4,6
    8
    6
    20
    0
    0
    34

    Итого
    10
    16
    48
    36
    10
    120



    Групповые средние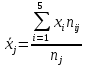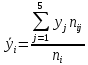





     
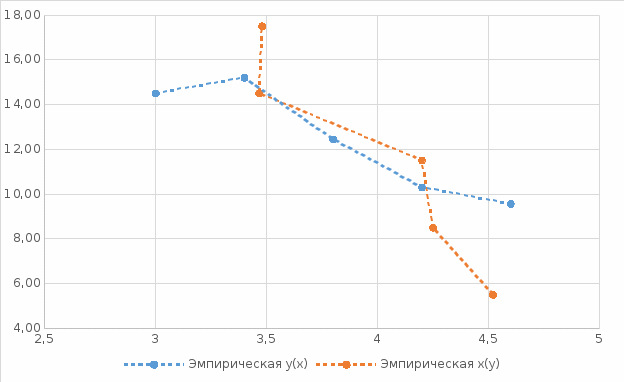    5,5
    8,5
    11,5
    14,5
    17,5
    Итого
    yсрi

    3
    0
    0
    0
    8
    0
    8
    14,50

    3,4
    0
    0
    2
    16
    8
    26
    15,19

    3,8
    0
    4
    16
    10
    2
    32
    12,44

    4,2
    2
    6
    10
    2
    0
    20
    10,30

    4,6
    8
    6
    20
    0
    0
    34
    9,56

    Итого
    10
    16
    48
    36
    10
    120
     

    xcpj
    4,52
    4,25
    4,20
    3,47
    3,48
     
     



    Уравнение линейной регрессии с y на x имеет вид:
    Уравнение линейной регрессии с x на y имеет вид:
    Найдем необходимые числовые характеристики.

    Выборочные средние:
    = (3*8 + 3.4(2 + 16 + 8) + 3.8(4 + 16 + 10 + 2) + 4.2(2 + 6 + 10 + 2) + 4.6(8 + 6 + 20))/120 = 3.953
    = (5.5(2 + 8) + 8.5(4 + 6 + 6) + 11.5(2 + 16 + 10 + 20) + 14.5(8 + 16 + 10 + 2) + 17.5(8 + 2))/120 = 12

    Дисперсии:

    σ2x = (32*8 + 3.42(2 + 16 + 8) + 3.82(4 + 16 + 10 + 2) + 4.22(2 + 6 + 10 + 2) + 4.62(8 + 6 + 20))/120 - 3.9532 = 0.26

    σ2y = (5.52(2 + 8) + 8.52(4 + 6 + 6) + 11.52(2 + 16 + 10 + 20) + 14.52(8 + 16 + 10 + 2) + 17.52(8 + 2))/120 - 122 = 9.65

    Откуда получаем среднеквадратические отклонения:

    σx = 0.512 и σy = 3.106

    и ковариация:

    Cov(x,y) = (4.2*5.5*2 + 4.6*5.5*8 + 3.8*8.5*4 + 4.2*8.5*6 + 4.6*8.5*6 + 3.4*11.5*2 + 3.8*11.5*16 + 4.2*11.5*10 + 4.6*11.5*20 + 3*14.5*8 + 3.4*14.5*16 + 3.8*14.5*10 + 4.2*14.5*2 + 3.4*17.5*8 + 3.8*17.5*2)/120 - 3.953*12 = -1.08

    Определим коэффициент корреляции:

    Связь между факторами заметная и обратная

    Запишем уравнения линий регрессии y(x):
    и вычисляя, получаем:

    yx = -4.11 x + 28.26

    Запишем уравнения линий регрессии x(y):
    и вычисляя, получаем:

    xy = -0.11 y + 5.29

    Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (3.953; 12) и точки расположены близко к линиям регрессии.

    С ростом жирности на 1% надои снижаются на 4,11 кг

    С ростом надоя на 1 кг жирность снижается на 0,11%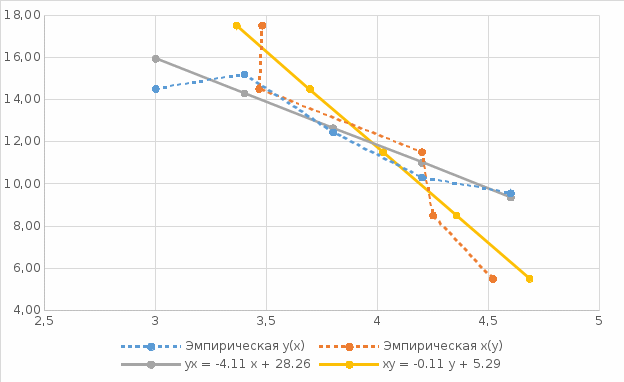


    Значимость коэффициента корреляции.

    =

    По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=120-m-1 = 118 находим tкрит:

    tкрит (n-m-1;α/2) = (118;0.025) = 1.98

    где m = 1 - количество объясняющих переменных.

    Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).

    Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим.

    F-статистика. Критерий Фишера.

    Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:

    Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.

    Далее определяют фактическое значение F-критерия:
    R2 = r2xy – для линейной регрессии
    где m=1 для парной регрессии.

    Табличное значение критерия со степенями свободы k1=1 и k2=118, Fтабл = 3.92

    Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).

    Оценим средний процент жирности молока для коров, дневной удой которых составляет 15 кг.

    xy = -0,11*15+5,29 = 3,64%








    1   2   3

    написать администратору сайта