4510321_Статистика. Вариант 2 Задача 1
 Скачать 80.9 Kb. Скачать 80.9 Kb.
|
ВАРИАНТ 2Задача 1.Всхожесть хранящегося на складе зерна в среднем составляет 80%, а среднее квадратическое отклонение 6%. Оценить вероятность того, что в выбранной партии зерна всхожесть составит: а) не менее 85%; б) не более 90%; в) будет отличаться от средней не более чем на 8%; г) будет отличаться от средней не менее чем на 10%. Вероятность попадания величины X в заданный интервал (α ; β). где Ф(x) — функция Лапласа а) P( 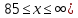 = Ф( = Ф(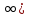 – Ф – Ф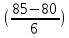 = 0,5-0,3 = 0,2 = 0,5-0,3 = 0,2б) P(- 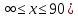 = Ф = Ф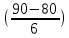 - Ф( - Ф(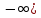 = 0,4525+0,5 = 0,9525 = 0,4525+0,5 = 0,9525в) Вероятность того, что отклонение нормально распределенной случайной величины от ее математического ожидания по абсолютной величине не превзойдет некоторого положительного числа δ, то есть |X- a| < δ, определяется так: г) P(- 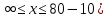 = Ф = Ф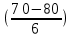 - Ф( - Ф(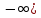 = -0,4525+0,5 = 0,0475 = -0,4525+0,5 = 0,0475P(80+10 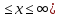 = Ф( = Ф(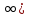 - Ф - Ф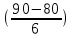 = 0,5 - 0,4525 = 0,0475 = 0,5 - 0,4525 = 0,0475вероятность того, что в выбранной партии зерна всхожесть будет отличаться от средней не менее чем на 10%. = 2*0,0475 = 0,095 Задача 2.Случайная величина ξ имеет нормальный закон распределения с параметрами а и 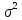 . Найти параметр . Найти параметр 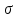 , если известно, что М(ξ)=5 и Р( 2< ξ< 8) = 0,9973. Вычислить вероятность того, что значение случайной величины ξ окажется меньше 0. , если известно, что М(ξ)=5 и Р( 2< ξ< 8) = 0,9973. Вычислить вероятность того, что значение случайной величины ξ окажется меньше 0.Построить графики функции распределения и функции плотности распределения этой случайной величины. a = М(ξ) = 5 s = 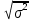 P(A < x < B) = Ф((B-а)/s) - Ф((A-а)/s) Ф(x) - Интегральная функция Лапласа P(2 < x < 8) = Ф((8-5)/s) - Ф((2-5)/s) = Ф(3/s) - Ф(-3/s), т.к. Ф(x) нечетная, то получим: Ф(3/s) +Ф(3/s) = 2Ф(3/s) = 0.9973 Ф(3/s) = 0.9973/2 = 0.4987 По таблице интегральной функции Лапласа найдем соответствующее значение аргумента = 3. Следовательно, s = 3/3 = 1 P(x < 0) = P(- 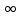 < x < 0) = Ф((0-5)/1) - Ф(- < x < 0) = Ф((0-5)/1) - Ф(- 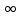 ) = Ф(-5) + Ф( ) = Ф(-5) + Ф(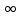 ) )Ф( 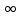 ) = 1/2 ) = 1/2Ф(-5) = 0.4999997 P(x < 0 ) = 1/2 - 0.4999997 = 0.0000003 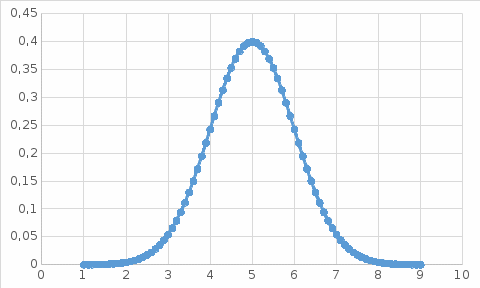 Рис. 1 Функция плотности распределения 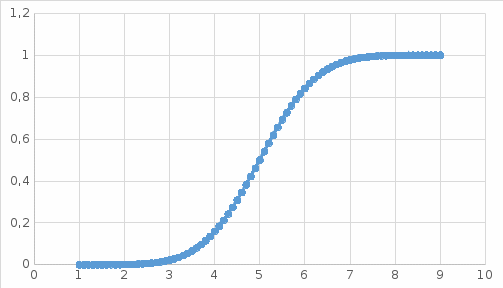 Рис. 2 Функция распределения Задача 3.Из 1560 сотрудников предприятия по схеме собственно случайной бесповторной выборки отобрано 100 человек для получения статистических данных о пребывании на больничном листе в течение года. Полученные данные представлены в таблице:
Найти: а) вероятность того, что среднее число дней пребывания на больничном листе среди сотрудников предприятия отличается от их среднего числа в выборке не более чем на 1 день (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля всех сотрудников, пребывающих на больничном листе не более 7 дней; в) объем бесповторной выборки, при котором те же границы для доли, (см. п. б)), можно гарантировать с вероятностью 0,98. Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Средняя взвешенная (выборочная средняя) ,2 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). = Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 7 в среднем на 2.546 Оценка среднеквадратического отклонения. Вероятность того, что абсолютная величина |X-a| отклонения окажется меньше δ. Вероятность того, что отклонение нормально распределенной случайной величины от ее математического ожидания по абсолютной величине не превзойдет некоторого положительного числа δ, то есть |X- a| < δ, определяется так: вероятность того, что среднее число дней пребывания на больничном листе среди сотрудников предприятия отличается от их среднего числа в выборке не более чем на 1 день (по абсолютной величине) = 0,318 Интервальное оценивание генеральной доли (вероятности события). Доверительный интервал для генеральной доли. (d - ε ; d + ε) 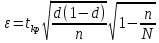 Доля всех сотрудников, пребывающих на больничном листе не более 7 дней d = (6+13+24)/100 = 0,43 Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа. В этом случае 2Ф(tkp) = γ Ф(tkp) = γ/2 = 0.95/2 = 0.475 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475 tkp(γ) = (0.475) = 1.96 границы, в которых с вероятностью 0,95 заключена доля всех сотрудников, пребывающих на больничном листе не более 7 дней (0.336; 0.524) Ф(tkp) = γ/2 = 0.98/2 = 0.49 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.49 tkp(γ) = (0.49) = 2.34 Объем выборки: 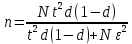 n = 1560*2,34^2*0,43*0,57/(2,34^2*0,43*0,57+1560*0,0939^2) = 139 чел. объем бесповторной выборки, при котором те же границы для доли (0.336; 0.524), можно гарантировать с вероятностью 0,98 равен 139 чел. |
