4510321_Статистика. Вариант 2 Задача 1
 Скачать 80.9 Kb. Скачать 80.9 Kb.
|
Задача 4.С целью изучения размера потребительских кредитов, выданных банком в одном из крупных магазинов электронной техники в течении последнего месяца по схеме собственно-случайной бесповторной выборки было отобрано 180 кредитов из 2500 выданных. Величины сумм выданных кредитов (тыс. руб.) представлены в таблице:
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот. По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану. Заменив параметры генеральной совокупности соответственно их наилучшими выборочными числовыми характеристиками и используя 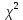 - критерий Пирсона, на уровне значимости а=0,05 проверить две гипотезы о том, что изучаемая случайная величина ξ - величина выданных кредитов - распределена: - критерий Пирсона, на уровне значимости а=0,05 проверить две гипотезы о том, что изучаемая случайная величина ξ - величина выданных кредитов - распределена:а) по нормальному закону распределения; б) по равномерному закону распределения. Построить на чертеже, на котором изображена гистограмма эмпирического распределения и соответствующие графики равномерного и нормального распределений. Определение числа групп. Число групп приближенно определяется по формуле Стэрджесса n = 1 + 3,2log n = 1 + 3,2log(180) = 8 Ширина интервала составит: xmax - максимальное значение группировочного признака в совокупности. xmin - минимальное значение группировочного признака. Таблица для расчета показателей.
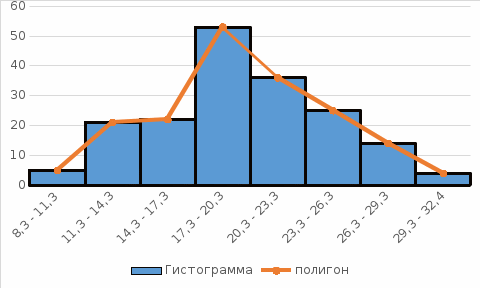 Рис. 1 Гистограмма и полигон Эмпирическая функция распределения.
Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. M[x] = 9.8*0.0278 + 12.8*0.117 + 15.8*0.122 + 18.8*0.294 + 21.8*0.2 + 24.8*0.139 + 27.8*0.0778 + 30.85*0.0222 = 19.884 Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]. D[X] = 9.82*0.0278 + 12.82*0.117 + 15.82*0.122 + 18.82*0.294 + 21.82*0.2 + 24.82*0.139 + 27.82*0.0778 + 30.852*0.0222 - 19.8842 = 22.701 Среднее квадратическое отклонение σ(x). Функция распределения F(X). F(x≤9.8) = 0 F(9.8< x ≤12.8) = 0.0278 F(12.8< x ≤15.8) = 0.117 + 0.0278 = 0.144 F(15.8< x ≤18.8) = 0.122 + 0.144 = 0.267 F(18.8< x ≤21.8) = 0.294 + 0.267 = 0.561 F(21.8< x ≤24.8) = 0.2 + 0.561 = 0.761 F(24.8< x ≤27.8) = 0.139 + 0.761 = 0.9 F(27.8< x ≤30.85) = 0.0778 + 0.9 = 0.978 F(x>30.85) = 1 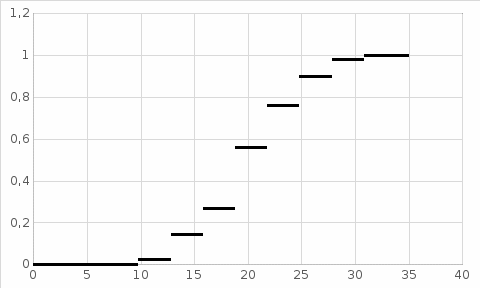 Рис. 2 Эмпирическая функция распределения Для оценки ряда распределения найдем следующие показатели: Средняя взвешенная (выборочная средняя) 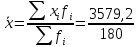 = 19,884 = 19,884Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота. Выбираем в качестве начала интервала 17.3, так как именно на этот интервал приходится наибольшее количество. Наиболее часто встречающееся значение ряда – 19.2 Медиана. Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше. В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 17.3 - 20.3, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот). Таким образом, 50% единиц совокупности будут меньше по величине 19.7. Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 3.9 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). = Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 19.9 в среднем на 4.765 Оценка среднеквадратического отклонения. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять. Степень асимметрии. Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Расчет центральных моментов проводим в аналитической таблице:
Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии. As = M3/s3 где M3 - центральный момент третьего порядка. s - среднеквадратическое отклонение. M3 = 1278.67/180 = 7.1 Положительная величина указывает на наличие правосторонней асимметрии Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя: Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) - отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3. M4 = 238680.34/180 = 1326 Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные - отрицательным эксцессом. Ex < 0 - плосковершинное распределение Проверка гипотез о виде распределения. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона. где pi - вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа где s = 4.765, xср = 19.9 Теоретическая (ожидаемая) частота равна fi = fpi, где f = 180 Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1)
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке). Kkp = χ2(8-2-1;0.05) = 11.07050; Kнабл = 7.64 Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью правила 3-х сигм. Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал: В нашем случае этот интервал составит: (19.9-3*4.765;19.9-3*4.765) = (5.605;34.195) Все значения величин попадают в интервал, так как xmin=8.3; xmax=32.4 Проверка гипотезы о равномерном распределении генеральной совокупности. Для того чтобы проверить гипотезу о равномерном распределении X,т.е. по закону: f(x) = 1/(b-a) в интервале (a,b) надо: 1. Оценить параметры a и b - концы интервала, в котором наблюдались возможные значения X, по формулам (через знак * обозначены оценки параметров): 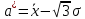 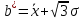 2. Найти плотность вероятности предполагаемого распределения f(x) = 1/(b* - a*) 3. Найти теоретические частоты: n1 = nP1 = n[f(x)*(x1 - a*)] = n*1/(b* - a*)*(x1 - a*) n2 = n3 = ... = ns-1 = n*1/(b* - a*)*(xi - xi-1) ns = n*1/(b* - a*)*(b* - xs-1) 4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы k = s-3, где s - число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s - число интервалов, оставшихся после объединения. 1. Найдем оценки параметров a* и b* равномерного распределения по формулам: 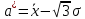 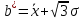 a* = 11,63; b* = 28,14 2. Найдем плотность предполагаемого равномерного распределения: f(x) = 1/(b* - a*) = 1/(28.14 - 11.63) = 0.0606 3. Найдем теоретические частоты: n1 = n*f(x)(x1 - a*) = 180 * 0.0606(11.3-11.63) = -3.62 Поскольку получилось отрицательное значение, то n1 = 0 n8 = n*f(x)(b* - x7) = 180 * 0.0606(28.14-29.3) = -12.69 Поскольку получилось отрицательное значение, то n8 = 0 Остальные ns будут равны: ns = n*f(x)(xi - xi-1)
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры a и b). Kkp(5,0.05) = 11.07050; Kнабл = 33.14 Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по равномерному закону. |
