мат. математика. Вариант 27 Задание 1 Решить задачу графическим методом. С подробным описанием всех действий, графиком и выводом. Задача
 Скачать 109.49 Kb. Скачать 109.49 Kb.
|
|
Вариант 27 Задание 1Решить задачу графическим методом. С подробным описанием всех действий, графиком и выводом. Задача: Для производства двух видов изделий А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется в течении 1 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 3 часа. Для производства единицы изделия В оборудование первого типа используется в течении 2 часов, оборудование второго типа – 3 часа, оборудование третьего типа – 1 час. На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 21 часа, оборудование второго типа 99 часов, оборудование третьего типа – 50 часов. Прибыль от реализации единицы готового изделия А составляет 4 денежные единицы, а изделия В – 2 денежные единицы. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решение: Под планом производства понимается ответ на простой вопрос: сколько изделий А и сколько изделий В надо выпустить, чтобы прибыль была максимальна. Прибыль рассчитывается по формуле: 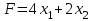 . .Запишем математическую модель задачи:  Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами Построим уравнение x1+2x2 = 21 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 10.5. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 21.. Построим уравнение 3x1+3x2 = 99 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 33. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 33. Построим уравнение 3x1+x2 = 50 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 50. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 16.67. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Рассмотрим целевую функцию задачи F = 4x1+2x2 → max. Построим прямую, отвечающую значению функции F = 4x1+2x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (4;2). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На рисунке 1 эта прямая обозначена пунктирной линией. 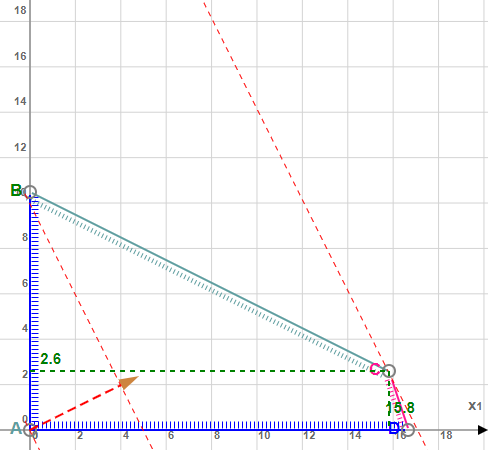 Рис. 1. Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:  Откуда найдем максимальное значение целевой функции: F(x) = 4*15.8 + 2*2.6 = 68.4 ден. ед. Ответ: F(x)=68,4 ден. ед. Задание 2Решить задачу симплексным методом. Все расчёты и таблицы представить в рукописном виде. Решение: А теперь решим эту задачу симплекс-методом. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам, введя дополнительные переменные 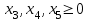 
Симплекс-таблица составляется так: В графе Базис записываются вектора переменных, принимаемые за базисные. На первом этапе это – х3, х4, х5. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных. В следующий столбец Сб записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов xi при i –й переменной. Под столбцом свободных членов записывается начальная оценка  Остальные оценки записываются под столбцами соответствующих векторов  . .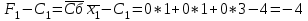  Следует отметить, что оценки для базисных векторов всегда равны нулю. Преобразование симплекс-таблицы ведется следующим образом: Шаг 1: Проверяется критерий оптимальности, суть которого состоит в том, что все оценки Fi-Ci должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу. Шаг 2: Для отрицательных оценок вычисляются величины     Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае -21 минимально, поэтому в качестве так называемого разрешающего элемента выбирается третий элемент первого столбца 3 (выделен в таблице). Шаг 3: Третья строка таблицы делится на 3 и вычитается из первой и второй строк. В сущности, применяется метод исключения неизвестных, известный как метод Жордана – Гаусса. Таким образом, новыми базисными переменными становятся x3, x4, x1. Возвращаемся к шагу 1 и повторяем весь процесс. Под столбцом свободных членов записывается начальная оценка  Остальные оценки записываются под столбцами соответствующих векторов  . .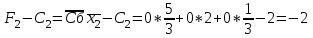  Следует отметить, что оценки для базисных векторов всегда равны нулю. Опять проверяется критерий оптимальности. Отрицательная оценка только одна – в столбце x2. Вычисляем:  Разрешающим элементом будет первый элемент второго столбца – 5/3. Новыми базисными переменными становятся х3, х2, х1 Делим вторую строку на 2 и вычитаем из третьей. Умножаем вторую строку на 5/2 и вычитаем из первой.     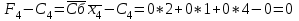 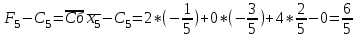 На этот раз отрицательных оценок нет, т.е. критерий оптимальности выполнен. Таким образом, получается искомое значение целевой функции F(13/5; 79/5; 0; 219/5; 0) = 342/5, т.е. возвращаясь к системе неравенств, получаем: F(x)= 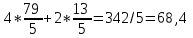 Ответ: F(x)=68,4 Задание 3На три базы A1, A2, A3 поступил очередной груз в количествах равных 140, 131, 149 ед. Этот груз требуется перевезти в четыре пунктов назначения B1, B2, B3, B4 в количествах 149, 90, 100, 81. Тарифы перевозок представлены матрицей
Найти план перевозок данной транспортной задачи методом северно-западного угла и минимального тарифа. Решение: Составим распределительную таблицу 1. Таблица 1 - Распределительная таблица
Для решения задачи необходимо выполнение следующего условия: cуммарные запасы продукции у поставщиков должны равняться суммарной потребности потребителей. Запасы поставщиков: 140 + 131 + 149 = 420 единиц продукции. Потребность потребителей: 149 + 90 + 100 + 81 = 420 единиц продукции. Суммарные запасы продукции у поставщиков равны суммарной потребности потребителей. Метод северо-западного угла. Начинаем заполнять таблицу от левого верхнего угла и постепенно "двигаемся" к правому нижнему.От северо-запада к юго-востоку. 140 = min { 149, 140 }
9 = min { 9, 131 }
90 = min { 90, 122 }
32 = min { 100, 32 }
68 = min { 68, 149 }
81 = min { 81, 81 }
Стоимость доставки продукции, для начального решения, не сложно посчитать. 140*2 + 9*8 + 90*4 + 32*1 + 68*3 + 81*6 = 1434 ден. ед. Метод наименьшей стоимости В первую очередь, будем задействовать маршруты с наименьшей стоимостью доставки. 100 = min { 100, 131 }
140 = min { 149, 140 }
31 = min { 90, 31 }
81 = min { 81, 149 }
59 = min { 59, 68 }
9 = min { 9, 9 }
Стоимость доставки продукции, для начального решения, не сложно посчитать. 140*2 + 31*4 + 100*1 + 9*9 + 59*7 + 81*6 = 1484 ден. ед. Список использованных источников1. Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие, - М.: Вузовский учебник, 2017. – 272 с. 2. Зайцев, М.Г. Методы оптимизации управления и принятия решений: примеры, задачи, кейсы / М.Г. Зайцев, С.Е. Варюхин. - М.: Дело АНХ, 2015. - 640 c. 3.Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – 2-е изд., испр. и доп. - М.: Вузовский учебник: ИНФРА-М, 2018. – 140 с. 4.Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебник для бакалавров. 3-е изд., перераб. и доп.- М.: Издательство Юрайт, 2018. – 304 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 .
.