ожоьжлждлжлж. ИНВЕСТИЦИИ ЗАДАЧИ ВАРИАНТ 5 реш. Вариант 5 (выполняют студенты, фамилии которых начинаются с букв Д, И, Л, С, Ч)
 Скачать 25.47 Kb. Скачать 25.47 Kb.
|
|
ВАРИАНТ 5 (выполняют студенты, фамилии которых начинаются с букв Д, И, Л, С, Ч) Задача 1. Предприниматель рассчитывает получить 250 тыс. руб. через 5 лет при 8% годовых. Сколько он должен вложить, если начисление процентов производится 1 раз в квартал? Решение Так как будущая стоимость определяется как: FV = PV* 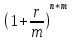 , где: , где:PV – первоначальная стоимость; r – ставка процента; m – число начислений в год (в данном случае m = 4); n – число лет начислений Отсюда PV = 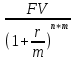 = = 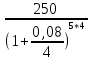 = = 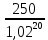 = 168,2 (тыс.руб.) = 168,2 (тыс.руб.)Ответ: чтобы через 5 лет получить 250 тыс.руб., предпринимателю необходимо вложить 168,2 тыс.руб. Задача 2. Определить курс акции (рыночная цена в расчете на 100 денежных единиц) продаваемой по цене 1300 руб., при номинале 1000 рублей. Решение Определим курс акции по формуле: Ка = 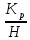 *100, где: *100, где: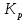 – рыночная цена; – рыночная цена;Н - номинал Ка = 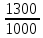 *100 = 130 (%) *100 = 130 (%)Ответ: курс акции равен 130 процентным пунктам. Задача 3. Предприятие рассматривает целесообразность приобретения новой технологической линии. На рынке имеется две модели со следующими параметрами (тыс. руб.):
Обоснуйте целесообразность приобретения той или иной технологической линии. Решение Рассчитаем чистую приведенную стоимость NPV проектов по формуле: NPV = 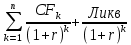 – IC , где: – IC , где: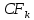 – денежные поступления по годам; – денежные поступления по годам;IC – инвестиционные вложения; r – норма прибыли; 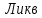 – ликвидационная стоимость – ликвидационная стоимостьОпределим NPV проекта 1: 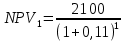 + + 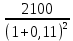 + +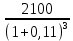 + +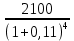 + +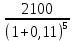 + +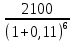 + + 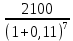 + +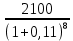 + + 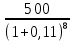 – 9500 = 1891,89+1704,41+1535,5+1383,34+1246,25+1122,75+1011,48+911,25 +216,96-9500 = 1523,82 (тыс.руб.) – 9500 = 1891,89+1704,41+1535,5+1383,34+1246,25+1122,75+1011,48+911,25 +216,96-9500 = 1523,82 (тыс.руб.)Определим NPV проекта 2: 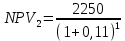 + + 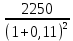 + +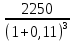 + +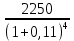 + +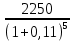 + +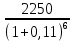 + + 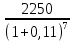 + +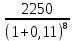 + + 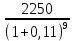 + +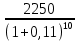 + + 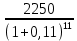 + +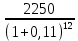 + + 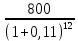 – 13000 = 2027,03 + 1826,15 + 1645,18 +1482,14 + 1335,27 + 1202,94 + 1083,73 + 976,33 + 879,58 + 792,42 + 713,89 + 643,14 + 228,67 – 13000 = 1836,47 (руб.) – 13000 = 2027,03 + 1826,15 + 1645,18 +1482,14 + 1335,27 + 1202,94 + 1083,73 + 976,33 + 879,58 + 792,42 + 713,89 + 643,14 + 228,67 – 13000 = 1836,47 (руб.)Так как NPV обоих проектов больше 0, то они являются экономически выгодными, однако NPV проекта 2 больше, поэтому именно его целесообразнее приобрести. Задача 4. Предприятие имеет возможность инвестировать до 90 тыс. руб. При этом цена капитала составляет 10%. Составьте оптимальный инвестиционный портфель из четырех альтернативных проектов, денежные потоки которых представлены следующей таблицей (тыс. руб.):
Решение Если данные проекты поддаются дроблению, то для каждого проекта рассчитываем индекс доходности: PI = 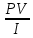 , где: , где:PV – настоящая стоимость денежных поступлений; I – сумма инвестиций в проект Рассчитаем чистый приведенный эффект (NPV) и индекс рентабельности для каждого проекта (PI):
Таким образом, по убыванию показателя PI проекты упорядочиваются следующим образом: В, С, D, A. Поэтому наиболее оптимальным будет следующий портфель:
Если рассматриваемые проекты дроблению не поддаются, оптимальный портфель определим перебором возможных вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта. Комбинация, максимизирующая суммарный NPV, будет оптимальной. В данном случае возможны варианты: А+B+C; A+C+D; B+C+D; A+B+D.
Тогда оптимальным является инвестиционный портфель, включающий проекты A, В и С. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
