физические основы теплоты. физические основы производства теплоты-5-14.11 (2). Вариант 5 Задача 4

• Название: Вариант 5 Задача 4
• Анкор: физические основы теплоты
• Дата: 22.11.2022
• Размер: 0.9 Mb.
• Имя файла: физические основы производства теплоты-5-14.11 (2).docx
• Тип: Задача; #806367

Вариант 5

Задача 4

На рисунке 6 дан график изменения состояния идеального газа в координатах (V,T). Представить этот процесс в координатах (P,T) и (P,V).



Решение:

Для того, чтобы представить целостный процесс 1-2-3-4 изменения состояния термодинамической системы в координатах (P,T) и (Р,V) необходимо рассмотреть каждый процесс отдельно с определением направления изменения (возрастания или уменьшения) всех термодинамических параметров, т.е.:

1-2– термодинамический процесс, при котором объем V– увеличивается, температура Т – увеличивается, давление Р– увеличивается.

2-3– изотермический процесс (Т = const), при котором объем V– уменьшается, давление Р– возрастает;

3-1 - изохорный процесс (V = const), при котором давление Т–уменьшается, давление – Р уменьшается;

2-4 – изохорный процесс (V = const), при котором давление Т–возрастает, давление – Р возрастает;

4-3– термодинамический процесс, при котором объем V– уменьшается, температура Т – уменьшается, давление Р– уменьшается.

Чертим координаты (P,T) и (Р,V) и изображаем на них процессы (рис. 1), соответствующие установленным изменениям термодинамических параметров.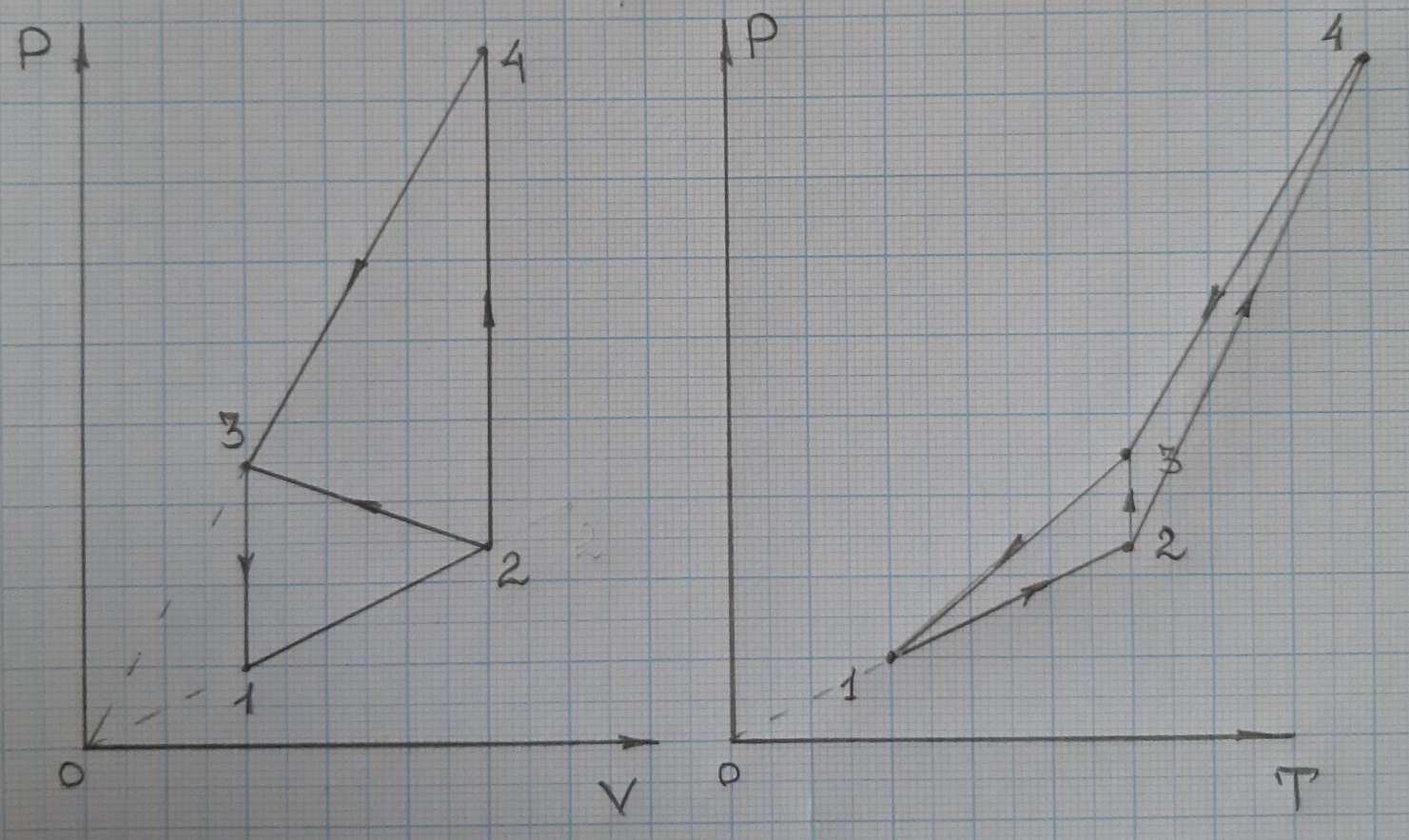



Рис. 1. Графики термодинамического процесса в координатах P-V и Р-Т

Задача 5

Азот массой m =2 кг занимает объем V₁ = 0,8 м³ и находится под давлением Р₁=1,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂ = 1,6 м³, а затем при постоянном объеме до давления Р₃ =1,5 МПа. Найти изменение ΔU внутренней энергии газа, совершенную им работу L и теплоту Q, переданную газу. Построить график процесса.

Решение:

1. Начальную и конечную температуру газа найдем из уравнения состояния идеального газа: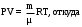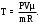



Произведем вычисления, учитывая, что для азота молярная маса равна μ = 28·10^-3 кг/моль.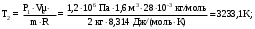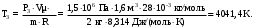







2. Работа расширения газа при постоянном давлении определяется по формуле: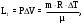



А работа газа, нагреваемого при постоянном объеме равна нулю:

L₂ = 0.

Следовательно, полная работа, совершаемая газом равна:

L = L₁ + L₂ = L₁.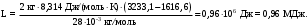



3. Изменение внутренней энергии газа равно: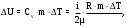



где i - число степеней свободы молекул газа; в данном случае для двухатомных молекул азота i = 5;

ΔТ = Т₃ -Т₁ - разность температур газа в конечном (третьем) и начальном (первом) состояниях.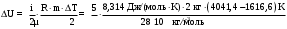





4. Согласно первому началу термодинамики, количество теплоты Q, переданное газу, равно сумме изменения внутренней энергии ΔU и работы L:

Q = ΔU + L = 3,6 МДж + 0,96 МДж = 4,56 МДж.

5. Строим график процесса (рис.2).



Рис. 2. График термодинамического процесса в координатах P-V

Ответ: изменение ΔU внутренней энергии газа равно 3,6 МДж, работу, совершаемая газом составит L = 0,96 МДж, а теплота, переданная газу Q = 4,56 МДж.

Задача 6

Холодильная машина работает по обратному циклу Карно, холодильный коэффициент которого равен 225 %. Каков термический КПД тепловой машины, работающей по прямому циклу Карно.
Решение:

КПД тепловой машины, работающей по обратному циклу Карно определяем по формуле: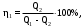



где Q₁ – количество теплоты, полученное от нагревателя;

Q₂ – количество теплоты, отданное холодильнику.

Тогда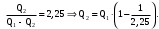



КПД тепловой машины, работающей по прямому циклу Карно определяем по формуле: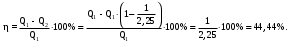



Ответ: термический КПД тепловой машины, работающей по прямому циклу Карно при заданных параметрах составит 44,44%.

Задача 7

В вертикальной трубе круглого сечения (r = 50 мм), высотой 7 м движется снизу вверх воздух. Определить коэффициент теплоотдачи от воздуха к стенке трубы, если средняя скорость воздуха 1,15 м/с, температура воздуха на входе 230 ^оС, на выходе температура равна 30 ^оС, средняя температура стенки 35^оС.

Решение:

1. Режим движения определяем по величине числа Рейнольдса: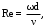



где ω – средняя скорость жидкости или газа, м/с;

d – характерный размер, м; в данном случае диаметр d = 2r =2· 0,05 = 0,1 м.

 – коэффициент кинематической вязкости, м²/с. Коэффициент кинематической вязкости воздуха находим при определяющей температуре, равной средней температуре воздуха, используя данные таблицы 12 Приложения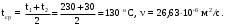



Тогда получим число Рейнольдса:



Поскольку1000 ˃ Rе = 4318 ˃ 2300, то режим движения воздуха переходный.
2. Для расчета критерия Нуссельта выбираем формулу - поток в трубе при Re = 2320 -10⁴:

Nu_ж = 7,6·ε₁·Рr^0,43·( Рr/Рr_с)^0,25,

где ε₁=1– поправочный коэффициент для длинных труб при l ˃ 50d (l/d = 700/10 = 70);

Физические параметры воздуха при определяющей температуре, равной 130 ⁰С (справочные данные):

t_возд = 130 ^оС;

 = 3,42·10^-2 Вт/(м·⁰С);

 = 26,63·10^-6 м²/сек;

Рr = 0,685.

Критерий Pr_с находим по тому же приложению, но при температуре стенки 35 ⁰С:

Рr_с = 0,700.

Тогда:

Nu_ж = 7,6·0,685^0,43·( 0,685/0,700)^0,25= 6,424.

3. Коэффициент теплоотдачи соответственно равен: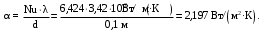



где α - коэффициент теплоотдачи, Вт/(м²∙К);

d - определяющий размер, м;

 - коэффициент теплопроводности, Вт/(м∙К).

Ответ: коэффициент теплоотдачи от воздуха к стенке трубы равен 2,197 Вт/(м²·К).

Задача 8

Определить коэффициент облученности и лучистый тепловой поток между двумя стальными параллельно расположенными дисками с центрами на общей нормали. Температуры поверхностей дисков 320 ^оС и 160 ^оС; диски имеют одинаковые диаметры, равные 460 мм; расстояние между ними h = 500 мм. Степень черноты дисков 0,28.

Решение:

1. Определим коэффициент облученности по формуле: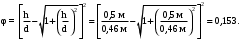



2. Площадь поверхности пластины составляет



3. Определим приведенную степень черноты: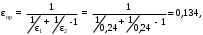



где ε₁ и ε₂ - степень черноты 1-го и 2-го тел.

4. Тепловой поток между пластинами определяем по формуле:



где С_s = 5,67 Вт/(м²·К⁴) - отношение коэффициентов лучеиспускания реального тела и абсолютно черного тела.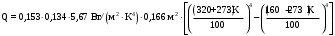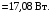





Ответ: в заданных условиях коэффициент облученности равен 0,153, а лучистый тепловой поток составляет 17,08 Вт.