фоэ 9. Электроника 9. Вариант 9 Задача 9

• Название: Вариант 9 Задача 9
• Анкор: фоэ 9
• Дата: 07.04.2022
• Размер: 0.66 Mb.
• Имя файла: Электроника 9.docx
• Тип: Задача; #451516
• страница: 3 из 5

Задача 59. Опишите метод определения типа носителей заряда с помощью термозонда. Определите тип электропроводности материала, основных и неосновных носителей. Нарисуйте зонную диаграмму данного материала. Какие примеси могут быть использованы? Селен. Стрелка вольтметра отклонилась влево.




Термозонд







V

Рис. 3

Тип проводимости можно измерить методом термозонда.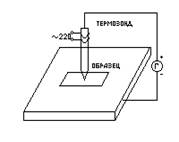



Образец помещается на массивную МЕ пластинку, служащую холодным контактом. Нагретым с помощью электронагревателя зондом касаются верхней поверхности образца. Если образец n-типа, то электроны в образце диффундируют от нагреваемой термозондом верхней грани к холодной нижней грани, заряжая ее отрицательно. Верхняя грань образца будет заряжаться положительно за счет остающихся нескомпенсированными ионов донорной примеси. Если образец p-типа, то к холодной грани образца диффундируют положительные дырки, оставляя на горячей грани отрицательный заряд нескомпенсированных ионов акцепторов. Таким образом, холодная грань образца заряжается знаком основных носителей заряда, который можно установить по направлению стрелки гальванометра в цепи термозонда. Еще можно определить тип проводимости из эффекта Холла по знаку коэффициента Холла, но метод термозонда более достоверный (точный) и поэтому он предпочтительнее.

Селен – довольно редкий химический элемент, который относится к неметаллам. Он черного цвета, обладает хрупкостью, на изломе блестит. Селен является аналогом серы. Открыл его Йенс Якоб Берцелиус в 1817 году. В ходе исследований, химик обнаружил, что селен, своими свойствами, похож на теллур, а так, как этот элемент в переводе с греческого – это Земля, то открытый элемент назвали именем её спутника – Луной. В виде самородков это вещество встречается очень редко. Получают селен из шлама медно-электролитного производства, в нем он содержится в составе селенида серебра. Для этого применяют множество различных способов.

Наиболее устойчивой модификацией данного вещества является серый селен или же металлический. Плавится он при температуре 217°C, кипит, примерно, при 685°C. Плотность серого селена составляет 4,79 г/см3.

Издавна селен нашел свое применение в стекольной и керамической промышленности. Его добавляют в стекольную массу, и он способствует её обесцвечиванию и устраняет зеленоватый оттенок, который возникает из-за примесей железосодержащих соединений. Селен способен придавать красный цвет керамическим и эмалированным изделиям, из соединения данного вещества с кадмием получается краситель, который используют в технологии изготовления рубинового стекла. Выступает это вещество и легирующей добавкой в металлургии. Сплавы, которые содержат его, имеют мелкозернистую структуру. В виде наполнителя селен применяется в резиновой промышленности.

Также, селен применяют при производстве полупроводниковой техники, ведь он обладает свойствами полупроводника р-типа. Сульфид кадмия является спутником данного материала и, вместе с ним образует p-n-переход. На их основе получают селеновые выпрямители.

Наделен селен ещё одним важным свойством – под действием света его электропроводность значительно увеличивается. Поэтому, этот материал используется при изготовлении селеновых фотоэлементов и других приборов, работающих по принципу внутреннего фотоэффекта. К ним относятся солнечная батарея и экспонометр.

Благодаря свойству селена – внутреннему фотоэффекту, были изобретены ксерографы – аппараты, при помощи которых, можно получить высококачественную черно-белую копию с оригинала. Эта технология применяется и в нынешнее время.

Пожалуй, полупроводниковые свойства селена и спровоцировали рост спроса на данный материал, а, как следствие, и его добычу.

Задача 67. Опишите эффект и метод Холла для определения типа носителей, концентрации и подвижности носителей. Определите тип электропроводности материала, основных и неосновных носителей. Нарисуйте зонную диаграмму данного материала. Какие примеси могут быть использованы?

Германий. Стрелка прибора отклонилась влево, индукция магнитного поля - по оси —Y. Куда направлен ток?

Одним из наиболее удобных методов изучения полупроводников является эффект Холла. Эффект состоит в возникновении на боковых гранях образца, помещенного в поперечное магнитное поле, разности потенциалов U_H, прямо пропорциональной величине тока i и индукции магнитного поля В:



U_H =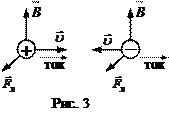



В формуле d – толщина образца;

Величина R_Н называется постоянной или сопротивлением Холла. Эффект Холла обусловлен взаимодействием носителей заряда (электронов проводимости и дырок) с магнитным полем. В магнитном поле на электрон действует сила Лоренца = e[ , ], на положительные заряды = q[ , ]. Здесь = /ne – средняя скорость направленного движения носителей в электрическом поле; n – концентрация носителей; e, q – электрические заряды электронов проводимости и дырок, которые при взаимодействии с магнитным полем отклоняются в направлении, перпендикулярном вектору плотности тока и вектору магнитной индукции .

В результате на боковой грани пластины происходит накопление зарядов и возникает электрическое поле Холла E_H = U_H/b. При одном и том же направлении тока на передней грани (ближе к нам) накапливаются разные по знаку заряды в зависимости от типа носителей. Например, если носители заряда – электроны, передняя грань заряжается отрицательно. Поле напряжённостью Е_H действует на электроны с силой F = еЕ_H, направленной против силы Лоренца. При F = F_Л поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Из условия равенства сил следует, что

еuB = eЕ_H,

и, сокращая, находим: Е_H = uB, или

U_H=bBu.

Учитывая, что u = ј/(ne), а j = i/S и принимая, что площадь торцевой поверхности датчика S = db,получим:

U_H = ,

Таким образом, теория приводит к выражению для U_H, совпадающему с формулой, установленной экспериментально.

Постоянная Холла оказывается при этом равной

R_H = , [м³/Кл].

Из формулы следует, что, зная численную величину и знак постоянной Холла, можно определить концентрацию и знак носителей тока в проводнике. У электронных проводников (n-типа) постоянная R_H отрицательна, у дырочных (p-типа) – положительна.

Зная удельную электропроводность проводника s = пеu, можно определить подвижность носителей заряда u .Подвижность носителей заряда представляет собой их среднюю дрейфовую скорость в электрическом поле единичной напряженности.

R_Hs = u.

Знак постоянной Холла определяется знаком носителей, подвижность которых выше. Обычно такими носителями являются электроны. Однако, при переходе к дырочной проводимости (например, у полупроводников р-типа) разность потенциалов Холла проходит через ноль и меняет знак. Проводимость химически чистых (беспримесных) полупроводников называется собственной проводимостью, а сами полупроводники – собственными полупроводниками. В отличие от собственных полупроводников, в которых проводимость осуществляется одновременно электронами и дырками, в примесных полупроводниках проводимость обусловливается, в основном, носителями одного знака: электронами в донорных полупроводниках (n-типа) и дырками в акцепторных полупроводниках (р-типа). Эти носители называются основными.

Помимо основных носителей полупроводник содержит всегда и неосновные: электронный полупроводник – дырки, а дырочный – электроны. Концентрация их, как правило, значительно ниже концентрации основных носителей. В эксперименте измерения поперечной (холловской) разности потенциалов U_H проводят дважды в противоположных направлениях и :

U_H1 = U_H + U_{H неосн.}

U_H2 = U_H + U_{H неосн.},

где U_{H неосн} – разность потенциалов, обусловленная неосновными носителями зарядов. Таким образом, холловская разность потенциалов определяется, как

U_H = (U_H1 + U_H2)/2.

В настоящей работе используется примесный полупроводник с концентрацией основных носителей зарядов, значительно большей концентрации неосновных носителей зарядов.

В настоящее время из полупроводниковых элементов наибольшее применение нашли германий и кремний. Германий является очень редким элементом: содержание его в земной коре составляет менее 7 -10^-4 %. Исходным продуктом для получения чистого германия является двуокись германия (GeO.,), восстанавливаемая в водороде.

Кремний, наоборот, — один из самых распространенных элементов в природе и запасы его неисчерпаемы. Однако получение чистого кремния затруднено из-за высокой температуры плавления (более 1400° С) и большой химической активности в жидком состоянии.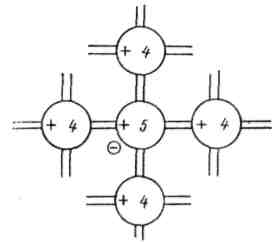



Кристаллическая решетка германия с примесью фосфора.

Если в четырехвалентный германий добавить пятивалентный мышьяк или фосфор (донорную примесь), то примесные атомы займут в кристаллической решетке места отдельных атомов германия. При этом около каждого атома примеси остается один валентный электрон, не связанный с окружающими атомами германия.

При температуре, отличающейся от абсолютного нуля, этот электрон может покинуть атом примеси и стать свободным, причем возникновение свободных электронов не связано с появлением дырки. Для ионизации атома чистого германия необходима энергия 0,72 эв, тогда как для ионизации примесного атома требуется энергия 0,015 эв. Поэтому уже при комнатной температуре все свободные электроны донорной примеси находятся в зоне проводимости. Германий с донорной примесью называется германием я-типа. Если к нему приложить электрическое поле, то в полупроводнике появится ток.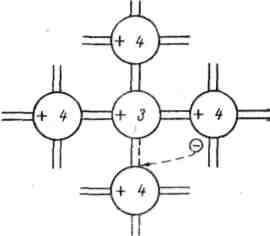



Кристаллическая решетка четырехвалентного германия с примесью трехвалентного индия.

В германии n-типа много свободных электронов, они рекомбинируют с дырками и уменьшают их количество; аналогично в германии р-типа много дырок, они рекомбинируют с электронами и уменьшают их количество.

При значительной концентрации примеси проводимость полупроводника определяется основными примесными носителями. Так, в германии n-типа основными носителями являются электроны, неосновными — дырки, а в германии р-типа основными носителями являются дырки, а неосновными — электроны.

Примесные полупроводники электрически нейтральны и обладают проводимостью, определяемой видом примеси.

При добавлении в четырехвалентный германий трехвалентного индия или галлия атом примеси,заняв место атома германия в кристаллической решетке, не будет иметь достаточного числа электронов для образования ко-валентной связи. При температуре выше абсолютного нуля один из валентных электронов соседних атомов, получив достаточную энергию, заполнит недостающую связь. Примесный атом становится отрицательным ионом, а в том месте, откуда ушел электрон, образуется дырка. При этом свободный электрон не появляется, количество свободных электронов в зоне проводимости остается прежним. Для того чтобы электрон от атома германия перешел к атому примеси, ему надо сообщить энергию порядка 0,1 эв, в то время как для того, чтобы электрону от примесного атома перейти в зону проводимости, надо затратить энергию в 0,72 эв. При обычной комнатной температуре большинство электронов германия переходит к примесным атомам. Германий с акцепторной примесью называется германием р-типа.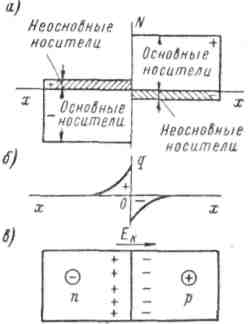




Задача 73. Опишите методику определения (схему, последовательность операций, формулы) ширины запрещенной зоны с помощью экспериментального определения зависимости: Удельной объемной проводимости от температуры.

При исследовании электрических свойств полупроводников и при производстве полупроводниковых материалов и приборов возникает необходимость в определении удельной электрической проводимости полупроводниковых материалов в виде слитков, образцов, пластин диффузионных и эпитаксиальных слоев.

Измерение удельной проводимости осуществляют не только для установления данного параметра при технологических процессах, но и также для определения косвенными методами других важных характеристик полупроводниковых материалов, например, ширины запрещенной зоны.

Четырехзондовый метод измерения удельной электрической проводимости является самым распространенным. Основное преимущество четырехзондового метода состоит в том, что не требуется создания омических контактов к образцу и возможно измерение удельной проводимости образцов самой распространенной формы и размеров. Условием для его применимости с точки зрения формы образца является наличие плоской поверхности, линейные размеры которой превосходят линейные размеры системы зондов. Многие особенности реальных образцов, связанные с их формой и характером условий на поверхностях, можно легко учесть, не создавая при этом трудностей для четырехзондового метода измерения.

Рассмотрим теоретические основы четырехзондового метода измерения удельной проводимости применительно к образцу, представляющему собой полубесконечный объем, ограниченный плоской поверхностью.

На плоской поверхности образца размещают четыре металлических электрода в виде металлических иголок - зондов с малой площадью соприкосновения. Все четыре зонда расположены вдоль одной прямой линии (рис 1). Через два внешних зонда (электрода) 1 и 4 пропускают электрический ток I, на двух внутренних зондах (электродах) 2 и 3 измеряют падение напряжения U2,3. По измеренным значениям разности потенциалов между зондами 2 и 3 тока, протекающего через зонды 1 и 4, можно определить величину удельной проводимости образца.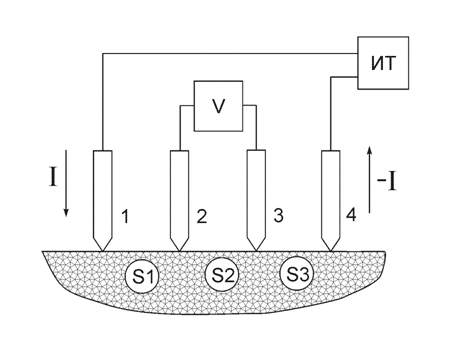



Рис.1. Схема измерения удельной электрической проводимости четырехзондовым методом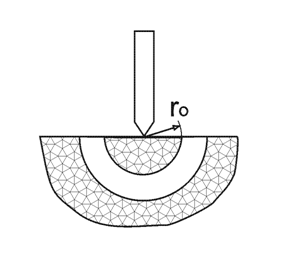



Рис.2. Модель зонда

Чтобы найти аналитическую связь между удельным сопротивлением ρ, током I и напряжением U2,3, необходимо решить более простую задачу, связанную с протеканием тока через отдельный точечный зонд, находящийся в контакте с плоской поверхностью полупроводникового образца полубесконечного объема (рис.2).

Так как распределение потенциала в образце имеет сферическую симметрию, для вычисления потенциала U(r) в объеме образца в зависимости от расстояния r до контакта достаточно решить уравнение Лапласа в сферической системе координат, в котором оставлен лишь член, зависящий от r: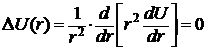

(1)

при условии, что потенциал в точке r=0 положителен и стремится к нулю при очень больших r. Интегрирование этого уравнения с учетом указанных граничных условий дает следующее решение: , где константу интегрирования можно определить из условия для напряженности электрического поля Е при некотором значении r=rо

(2)

где – плотность тока, протекающего через полусферу радиусом rо.

Окончательно получим

(3)

В практике нашли применение лишь две конструкции зондовых головок. Это случаи расположения зондов в линию (рис. За) и по углам прямоугольника (рис.3б).

Выражение (3) справедливо лишь для полубесконечых образцов. Это значит, что границы образца как в плоскости расположения зондов, так и по глубине образца удалены от зондов на бесконечность. В реальных случаях за счет конечности образцов удельное сопротивление будет определяться в виде

(4)

где F1 – поправочный множитель, являющийся функцией межзондового расстояния l, толщины образца d и расстояния от зондов до ближайшей границы образца L, К=πl.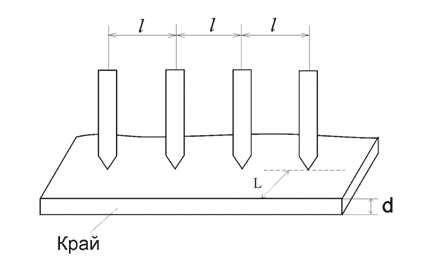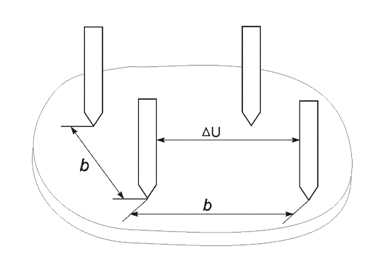



а) б)

Рис.3. Различные способы расположения зондов на поверхности образца

Электрическая схема измерения удельной проводимости четырехзондовым методом весьма проста (см. рис.1). Ток I от регулируемого источника постоянного тока ИТ пропускается через зонды 1 и 4. Желательно, чтобы источник тока имел высокое выходное сопротивление, т. е. являлся генератором тока. Напряжение, возникающее при этом на зондах 2 и 3, измеряется вольтметром V. Чтобы контактные сопротивления зондов не оказывали влияния на результаты измерений, разность потенциалов U2,3 необходимо измерять в отсутствие тока через них. Поэтому измерения проводят компенсационным методом. В зависимости от сопротивления образцов в качестве компенсаторов используют низкоомные или высокоомные потенциометры постоянного тока и в качестве нуль-индикаторов - высокочувствительные гальванометры. Исключить термо-э. д.с., возникшую вдоль образца, можно проведя измерения при двух противоположных направлениях тока. При этом разность потенциалов вычисляется как среднее из результатов двух измерений.

Возможно также применение электронных вольтметров с высоким входным сопротивлением. В таком случае ток через измерительные зонды пренебрежимо мал, что позволяет отказаться от использования компенсационных методов измерений. Применение милливольметра с входным сопротивлением порядка 108Ом дает возможность измерять удельное сопротивление на слитках и пластинах кремния до 3000Ом·см, можно измерять практически любые полупроводниковые материалы.

Обычно измерения проводят при токе порядка 1 мА или меньше, причем точное значение тока находят путем измерения падения напряжения на эталонном сопротивлении, включенном последовательно в цепь зондов 1 и 4. Наименьший рабочий ток определяется возможностью измерения малых напряжений, наибольший рабочий ток ограничивается нагревом образца, что наиболее существенно для низкоомных образцов.

Расстояние между зондами выбирают 0,5-2,0мм. Зонды монтируют в специальной четырехзондовой головке, где расстояния между зондами строго фиксированы. Для изготовления зондов используют вольфрамовую проволоку или проволоку из твердых сплавов ВК-10, ВК-16 и ВК-20. Концы зондов затачивают электролитически или путем электроэрозионной обработки и полировки с применением алмазных порошков так, чтобы диаметр контакта был значительно меньше рассеяния между ними. Если диаметр контакта составляет 0,05S или меньше, то погрешность измерения, обусловленная конечными размерами контактов, составляем менее 2%. Надежный самоустанавливающийся контакт каждого зонда с поверхностью образца обеспечивается за счет пружин. Величина давления на контакт не оказывает существенного влияния на результаты измерений, однако большое давление может повредить образец или зонд. Четырехзондовую головку крепят к манипулятору, с помощью которого головка устанавливается на поверхности образца.

Для получения малых величин контактных сопротивлений металлических зондов поверхность образца, на которой производят измерения, механически обрабатывают (например, шлифуют и полируют).

Удельная электрическая проводимость полупроводникового материала в области собственной элекропроводимости

(5)

где ni - концентрация носителей заряда в области собственной электропроводности;

(6)

No, Nv - эффективные плотности квантовых состояний в свободной и валентной зонах соответственно;

Eg – ширина запрещенной зоны;

К – постоянная Больцмана;

Т – абсолютная температура;

Un, Up – подвижность электронов и дырок.

Величина (No,· Nv )1/2, как известно, пропорциональна Т3/2. Примем, что зависимости подвижности электронов и дырок от температуры одинаковы и что каждая из подвижностей в достаточно широком интервале температур может быть представлена степенной функцией температуры:

(7)

В действительности температурные зависимости подвижности электронов и дырок отличаются друг от друга, т. е. характеризуются различными значениями α.

С учетом (7) отношение подвижностей В=Un/Up представляет собой константу, не зависящую от температуры. При сделанных допущениях σi можно записать в виде произведения температурно зависимых сомножителей на некоторую постоянную, величину:

(8)

Логарифмируя выражение (8) и строя график зависимости

(9)

определяем ширину запрещенной зоны Eg из значения производной функции



(10)

Окончательно ширина запрещенной зоны (в эВ)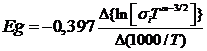

(11)

Как следует из (11), для определения Eg необходимо знать значение α. Однако, практически в ряде случаев α не сильно отличается от 3/2, так что сомножителем можно пренебречь.