Решение вариант ЕГЭ. Вариант Часть 1
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
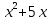 =- =- 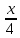 , находим a = 0, a =- , находим a = 0, a =- 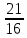 . Выкалываем эти тоски (рис.). По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при , a =- . Выкалываем эти тоски (рис.). По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при , a =- 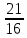 , a = 0, a = , a = 0, a = 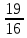 , a = , a = 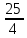 . .Отв: - 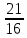 ; 0; ; 0; 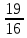 ; ; 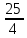 .▲ .▲Вар. 13. Найдите все значения а, при каждом из которых система 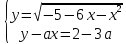 имеет ровно два решения. имеет ровно два решения.▼ Построим график уравнения 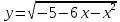 , ,Преобразовав подкоренное выражение, получим 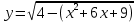 , , 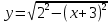 . .Если y ≥ 0, то y2 = 22 – (x + 3)2, (x + 3)2 + y2 = 22. Если y < 0, точек, удовлетворяющих уравнению, нет. Получилась полуокружность с центром в точке (-3; 0) радиусом 2, лежащая в верхней полуплоскости (рис.) Уравнение 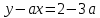 запишем в виде запишем в виде 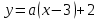 -семейство -семействопрямых с угловым коэффициентом а, проходящих через точку М(3; 2). Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если a1 <a a2. Прямая ВМ касается окружности и является горизонтальной, поэтому ее угловой коэффициент равен 0, значит a1 = 0. Найдем a2 из условия, что прямая АМ 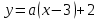 проходит через точку А(-5; 0). проходит через точку А(-5; 0).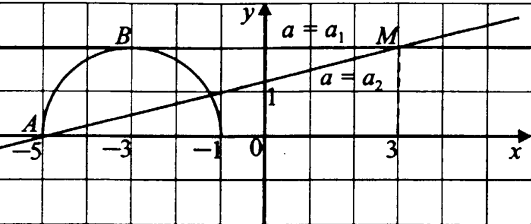 а(-5 – 3) + 2 = 0, а = 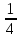 . Следовательно, система имеет ровно два решения при 0 <a . Следовательно, система имеет ровно два решения при 0 <a 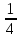 . .Отв: (0; 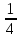 ] ▲ ] ▲Вар. 17. При каких значениях параметра а система 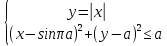 имеет два решения? имеет два решения?▼ Заметим, что при a < 0 неравенство не имеет решения, потому что левая часть неравенства отрицательна. При а = 0 оно имеет вид x2 + y2 0 и имеет единственное решение x = y = 0. Рассмотрим а > 0. Решим задачу, построив графики уравнения и неравенства. Графиком неравенства системы будет являться круг радиусом 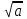 с центром в точке (sina; a). с центром в точке (sina; a).Графиком уравнения будут стороны угла (см. рис.). Ровно два решения будет, если круг касается обеих сторон угла, тогда центр круга должен лежать на биссектрисе угла, то есть на луче Oy. Значит, абсцисса центра круга должна равняться нулю, sina = 0, a = k. a = k. Значит, aZ. Рассмотрим О1МО, где О1 – центр круга, М – одна из точек касания. Тогда О1О = а, О1М = 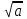 , О1МО = 90°, О1ОМ = 45°. Отсюда, , О1МО = 90°, О1ОМ = 45°. Отсюда, О1М = О1ОsinО1ОМ = 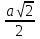 . Следовательно, . Следовательно, 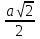 = = 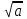 , , 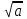 = = 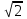 , а = 2. Ясно, что 2Z. , а = 2. Ясно, что 2Z.Oy 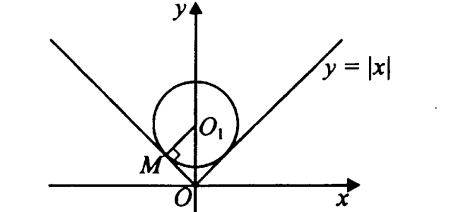 Отв: 2▲ 19) На доске записаны числа 4, 5, 6, 7, 8, 9,..,18. За один ход разрешается стереть произвольно три числа, сумма которых меньше 32 и отлична от каждой из сумм троек чисел, стертых на предыдущих ходах. а) Приведите пример последовательных трех ходов. б) Можно ли сделать 5 ходов? в) Какое наибольшее число ходов можно сделать? ▼ а) Пример последовательных трех ходов (стерты тройки чисел): (4, 7, 10); (5, 8, 11); (6, 9, 12)    |
