Решение вариант ЕГЭ. Вариант Часть 1
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
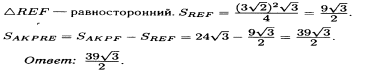 Вар.5.  ▼ 15) Вар1. Решите неравенство 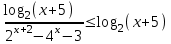 . .▼ ОДЗ: 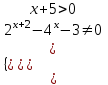 ; ; 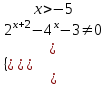 ; ; 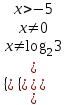 . .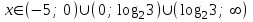 . .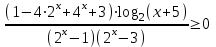 , , 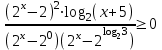 . .Применим МЗМ: 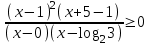 , , 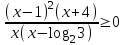 Отв: x[-4; 0){1}(log23; )▲ Вар5. Решите неравенство 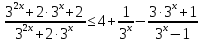 . .▼ Обозначим 3x= t, t > 0. Неравенство примет вид: 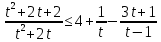 , , 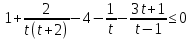 , ,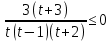 . Воспользуемся условием t > 0. . Воспользуемся условием t > 0.Так как при этомt + 3 > 0 и t + 2 > 0, то неравенство верно при t – 1 < 0, то есть 0 < t < 1. Тогда 0 < 3x < 1, x < 0. Отв: (-∞; 0)▲ Вар.9. Решите неравенство 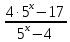 + +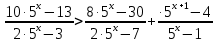 ▼ С помощью замены 5x= t, t > 0, приведем неравенство к виду 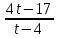 + +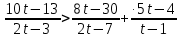 . Выделим целую часть в каждом слагаемом: . Выделим целую часть в каждом слагаемом: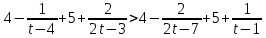 , , 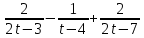 - - 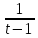 > 0. > 0.После приведения к общему знаменателю и упрощения получим: 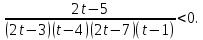 Решим неравенство методом интервалов Решим неравенство методом интервалов , С учетом условия t > 0, получим 0 < t < 1, 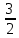 < t < < t < 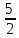 , , 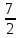 < t < 4. < t < 4.Возвращаясь к переменной х, получим 5x < 1, 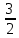 < 5x < < 5x < 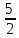 , , 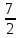 < 5x < 4, откуда < 5x < 4, откуда x < 0, 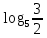 < x < < x < 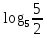 , , 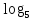 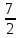 < x < < x < 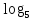 4. 4.\Отв: (-∞; 0)( 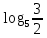 ; ; 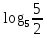 )( )(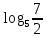 ; ; 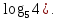 Вар. 13. Решите неравенство 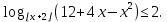 ▼ ОДЗ: 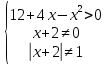 , , 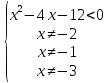 , , 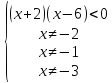 , ,x(-2; -1)(-1; 6). 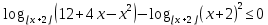 . .На ОДЗ заменим полученное неравенство равносильными неравенствами, применив дважды метод рационализации: знак logaf – logag совпадает со знаком (a – 1)(f – g), знак f – g совпадает со знаком (f – g)(f + g). Согласно 1: (x+2 - 1)(12 + 4x – x2 – x2 – 4x – 4) 0. (x+2 - 1)(– 2x2 + 8) 0. Разделим обе части неравенства на -2 (x+2 - 1)( x2 - 4) ≥ 0. Согласно 2: (x + 2 – 1)(x + 2 + 1) )( x2 - 4) ≥ 0. (x + 1)(x + 3)(x – 2)(x + 2) ≥ 0. Решение неравенства показано на рисунке  \ \x -3, -2 x -1, x ≥ 2. Учитывая ОДЗ, получим:  -2 < x< -1; 2 x < 6. Отв: (-2; -1)[2; 6)▲ Вар. 13. Решите неравенство 72x – 7x+1 + 37x - 5 ≥ 6. ▼ Введем обозначение 7x = t, t > 0. Неравенство примет вид t2 – 7t + 3t - 5 ≥ 6. 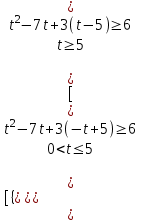 ; ; 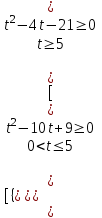 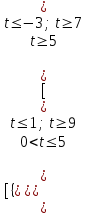 ; ; 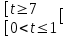 . .1) 0 < 7x ≤ 1, x ≤ 0. 2) 7x ≥ 7, x ≥ 1. Значит, объединением решений будут промежутки (-; 0] и [1; ) Отв: (-; 0][1; ) ▲ 16) В треугольнике АВС с прямым углом С MN – средняя линия, параллельная стороне АС. Биссектриса угла А пересекает луч MN в тоске K. а) Докажите, что BKC AMK. б) Найдите отношение SBKC:SAMK, если cosBAC = 0,6. ▼ 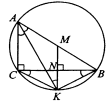    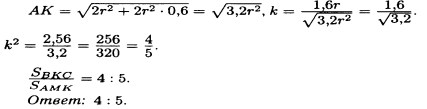  17) В июле 2016 года планируется взять кредит в банке на сумму S млн рублей, где S – целое число, на 4 года. Условия возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
Найдите наименьшее значение S, чтобы общая сумма выплат была больше 20 млн рублей. ▼ Пусть x1, x2,x3,x4 – ежегодные выплаты. Составим уравнения, которые соответствуют графику погашения кредита: на 2017 год 1,2S - x1 = 0,7S, на 2018 год 1,20,7S - x2 = 0,4S, на 2019 год 1,20,4S - x3 = 0,2S, на 2020 год 1,20,2S - x4 = 0S. Сложим все уравнения 1,2S(1+ 0,7 + 0,4 + 0,2) – (x1 +x2 +x3 +x4) = S(0,7 + 0,4 + 0,2). Пусть Х = x1 +x2 +x3 +x4 – общая сумма выплат. Уравнение примет вид 1,2S2,3 – Х = 1,2S, Х = S(2,76 – 1,3) = 1,46S, 1,46S > 20, S > 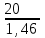 = = 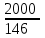 = =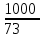 = =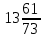 . .Так как S – целое число, то наименьшее значение S составляет 14 млн рублей. Отв: 14  18). Вар 1. Найдите все значения а, при каждом из которых уравнение 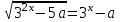 имеет единственный корень. имеет единственный корень.▼ Пусть 3x = t, t > 0, тогда 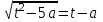 . .При t – a < 0 правая часть уравнения отрицательная, а левая – неотрицательная, поэтому уравнение при t < a решения не имеет. При t – a ≥ 0 получаем t2 – 5a = t2 – 2at + a2, 2at = a2 + 5a. При a= 0: 0t = 0 – любое положительное значение t является корнем уравнения, что противоречит условию единственности корня. При a 0: t = 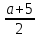 . Для этого корня должны выполняться условия: t≥ a и t > 0. . Для этого корня должны выполняться условия: t≥ a и t > 0.Условие 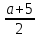 ≥ a выполняется при а ≤ 5. ≥ a выполняется при а ≤ 5.Условие 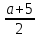 > 0 выполняется при а > -5. > 0 выполняется при а > -5.Исходное уравнение имеет единственный корень при -5 < a < 0 и 0 < a ≤ 5. Отв: (-5; 0)(0; 5].▲ Вар 5. Найдите все значения а, при каждом из которых уравнение x2 + ax + 4 = 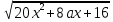 имеет ровно три различных корня. имеет ровно три различных корня.▼ Исходное уравнение при x2 + ax + 4 < 0 не имеет корней. При x2 + ax + 4 ≥ 0 (*) можно обе части исходного уравнения возвести в квадрат. (x2 + ax + 4)2 = 20x2 + 8ax + 16. x4 + 2aх3 + х2(а2 – 12) = 0, x2(x2+ 2aх + а2 – 12) = 0, x2((x+а)2– 12) = 0, х1 = 0, (x+а– 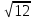 )(x+а+ )(x+а+ 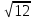 ) = 0, ) = 0,х2 = -а + 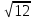 , х3 = -а - , х3 = -а - 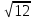 . .Чтобы исходное уравнение имело три различных корня, необходимо выполнение условия (*) для чисел х1, х2, х3 и выполнения условия, что эти числа различны. х2 ≠ 0, х3 и х3 ≠ 0, если а ≠ 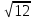 = 2 = 2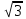 , и а ≠ - , и а ≠ -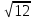 = -2 = -2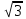 . .Обозначим g(x) =x2 + ax + 4. g(x1) = g(0) = 4 > 0. Числа х2 = -а + 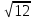 , и х3 = -а - , и х3 = -а - 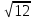 будут корнями исходного уравнения, если выполняются условия: будут корнями исходного уравнения, если выполняются условия: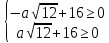 ; ; 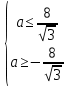 ; ; Таким образом, а- 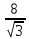 ;-2 ;-2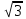 )( -2 )( -2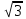 ; 2 ; 2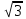 )(2 )(2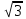 ; ; 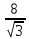 ]. ].Отв: - 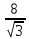 ;-2 ;-2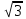 )( -2 )( -2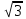 ; 2 ; 2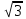 )(2 )(2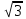 ; ; 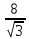 ].▲ ].▲Вар 9. Найдите все значения а, при каждом из которых уравнение 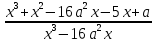 = 1 имеет единственный корень. = 1 имеет единственный корень.▼ В левой части уравнения выделим целую часть 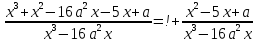 . Тогда уравнение имеет вид . Тогда уравнение имеет вид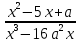 . = 0. Оно равносильно системе . = 0. Оно равносильно системе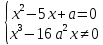 ; ;  ; ; Решим систему графически в системе координат хОа. Для этого построим графики функций 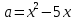 и и 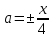 . .Графиком функции 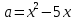 является парабола, ветви которой направлены вниз. Вершина параболы – точка ( является парабола, ветви которой направлены вниз. Вершина параболы – точка (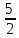 ; ;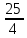 ), точки (0; 0) и (5; 0) принадлежат параболе. Графиком функции ), точки (0; 0) и (5; 0) принадлежат параболе. Графиком функции 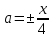 являются прямые являются прямые 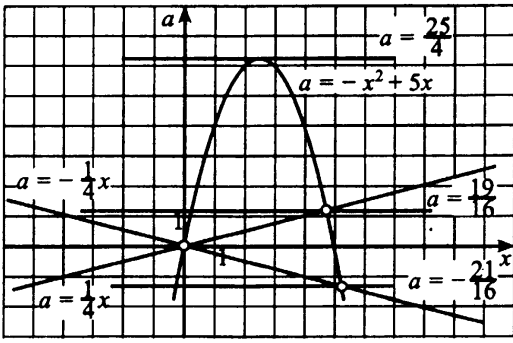 Решая уравнение – 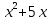 = = 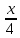 , находим точки пересечения прямой , находим точки пересечения прямой 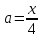 и параболы и параболы 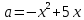 : х = 0, х = : х = 0, х = 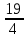 , откуда a = 0, a = , откуда a = 0, a = 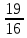 . Аналогично, решая уравнение – . Аналогично, решая уравнение – |
