Решение вариант ЕГЭ. Вариант Часть 1
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
Вар.17. Цена телевизора ежеквартально (в квартале – три месяца) уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый квартал уменьшилась цена телевизора, если выставленный на продажу за 50000 рублей через два квартала был продан за 41405 рублей? ▼ Цена телевизора первоначально была 50000 руб. Через квартал она стала 50000 - 50000·0,01х = 50000(1 – 0,01х), где х – количество процентов, на которые уменьшается ежеквартально цена телевизора. Через два квартала его цена стала 50000(1 – 0,01х)2. Составим и решим уравнение: 50000(1 – 0,01х)2 = 41405, (1 – 0,01х)2 = 0,8281, (1 – 0,01х) = 0,91, х = 9. Итак, на 9 процентов уменьшалась цена телевизора ежеквартально. Отв: 9 ▲ 12) Вар.1. Рассмотрите функцию 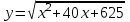 и найдите ее наименьшее значение. и найдите ее наименьшее значение.▼ Для неотрицательных t функция 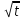 возрастает, значит, возрастает, значит, 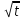 наименьшее при наименьшем значении t. Преобразуем выражение под знаком корня. наименьшее при наименьшем значении t. Преобразуем выражение под знаком корня.Заметим, что 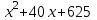 = = 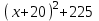 ≥ 225, причем при х = -20 достигается равенство. ≥ 225, причем при х = -20 достигается равенство.Отсюда 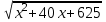 ≥ ≥ 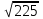 = 15. При х = -20 имеем ymin = 15. = 15. При х = -20 имеем ymin = 15.Отв: 15. ▲ Вар.5. Найдите точку максимума функции y = 2x3 + 40x2 + 200x + 79. ▼ Найдем производную исходной функции y(x) = 6x2 + 80x + 200. Найдем нули производной из уравнения y(x) = 0: 6x2 + 80x + 200 = 0, 3x2 + 40x + 100 = 0 х1 = -10, х2 = -10. Расставим знаки производной и определим промежутки монотонности исходной функции Из рисунка видно, что значение х = -10 является единственной точкой максимума. Отв: -10. ▲ Вар.9. Найти точку максимума функции 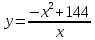 . .▼ ОДЗ: х ≠ 0. y = -x - 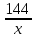 , тогда производная исходной функции y(x) = -1 + , тогда производная исходной функции y(x) = -1 + 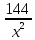 . Найдем нули производной y(x) =0 при . Найдем нули производной y(x) =0 при 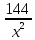 = 1, х2 = 144, х =12. Расставим знаки производной и определим промежутки монотонности исходной функции. = 1, х2 = 144, х =12. Расставим знаки производной и определим промежутки монотонности исходной функции.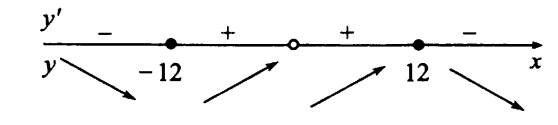 Из рисунка видно, что исходная функция имеет единственную точку максимума х = 12. Отв: 12. Вар. 13. Найдите точку максимума функции y = (x + 7)2(x - 6) + 11. ▼ Найдем производную исходной функции, используя формуле производной произведения: y(x) = (x + 7)(3x - 5). Отыщем нули производной: y(x) = 0, (x + 7)(3x - 5) = 0 х1 = -7, х2 = 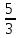 . Расставим знаки производной и определим промежутки монотонности исходной функции: . Расставим знаки производной и определим промежутки монотонности исходной функции: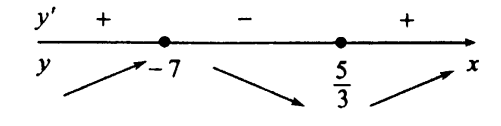 Из рисунка видно, что х = -7 является единственной точкой максимума Отв:-7▲ Вар. 17. Найдите наибольшее значение функции y = ln(x + 7)9 – 9x на отрезке [-6,5; 0]. ▼ ОДЗ: (x + 7)9 > 0. x + 7 > 0, x > -7. Так как на ОДЗ ln(x + 7)9 = 9ln(x + 7), то исходная функция примет вид y = 9ln(x + 7) – 9x. Найдем производную: y = 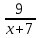 – 9. Определим нули производной – 9. Определим нули производной 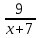 – 9 = 0, – 9 = 0, 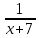 – 1, х = -6. – 1, х = -6.Расставим знаки производной и определим промежутки монотонности исходной функции  Из рисунка видно, что на отрезке [-6,5; -6] исходная функция возрастает, а на отрезке [-6; 0] – убывает, Таким образом, наибольшее значение на отрезке [-6,5; 0] достигается при х = -6 и равно y(-6) = ln(-6 + 7)9 - 9·(-6) = 54. Отв: 54 ▲ 13) Вар.1. а) Решите уравнение 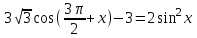 б) Укажите корни этого уравнения, принадлежащие отрезку [2π; 3π]. ▼ а) Запишем уравнение в виде 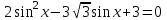 . Решая это уравнение как квадратное относительно sinx, получим . Решая это уравнение как квадратное относительно sinx, получим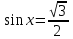 ; ; 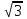 Уравнение Уравнение 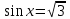 >1 – корней не имеет. >1 – корней не имеет. 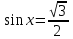 , , 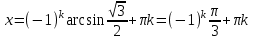 . .б) При ответах на дополнительные вопросы удобно представить решение в виде х = 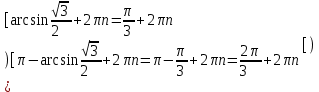 . .Укажем корни, которые лежат в промежутке [2π; 3π]: 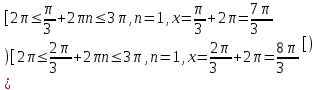 . .Отв: а) 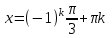 ; б) ; б) 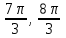 .▲ .▲Вар.5. а) Решите уравнение 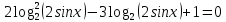 . .б) Найдите все корни этого уравнения, принадлежащие отрезку [ 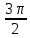 ; 3π]. ; 3π].▼ а) Обозначим log2(2sinx) = t. 2t2 – 3t + 1 = 0 t1 = 1, t2 = ½. 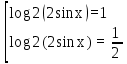 ; ; 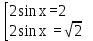 ; ;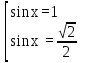 ; ; 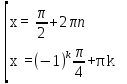 ; ;б) Корни, принадлежащие отрезку [ 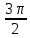 ; 3π], найдем с помощью числовой окружности: ; 3π], найдем с помощью числовой окружности: 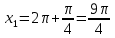 ; ; 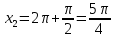 ; ; 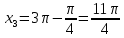 . .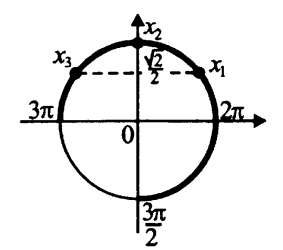 Отв: а) 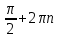 ; ; 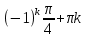 ; б) ; б) 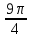 ; ; 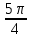 ; ; 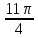 .▲ .▲Вар. 9. а) Решите уравнение 9·32cosx - 10 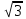 ·3cosx + 3 =0. ·3cosx + 3 =0.б) Укажите корни этого уравнения, принадлежащие отрезку [ 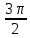 ; 4π]. ; 4π].▼ а) После замены t = 3cosx исходное уравнение примет вид 9t2 – 10 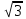 t + 3 = 0. Корни этого уравнения t1 = t + 3 = 0. Корни этого уравнения t1 = 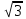 , t2 = , t2 = 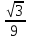 . Возвращаясь к переменной х, получим . Возвращаясь к переменной х, получим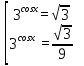 ; ; 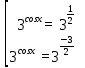 ; ; 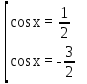 ; ;Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим 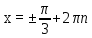 . .б) Запишем уравнение в виде 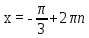 или или 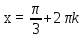 и выясним, для каких целых значений n и k справедливы неравенства и выясним, для каких целых значений n и k справедливы неравенства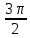 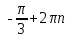 4π и 4π и 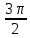 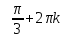 4π. 4π.Получим 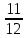 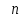 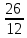 и и 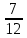 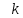 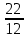 . Отсюда следует, что два целых значения . Отсюда следует, что два целых значения 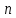 = 1 и = 1 и 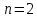 удовлетворяют неравенству удовлетворяют неравенству 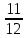 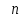 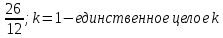 , удовлетворяющее неравенству , удовлетворяющее неравенству 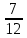 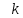 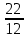 . .При 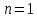 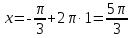 . .При 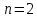 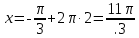 При 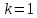 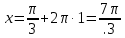 . .Итак, 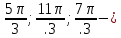 корни уравнения, принадлежащие промежутку [ корни уравнения, принадлежащие промежутку [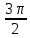 ; 4π]. ; 4π].……………………… Отв: а) 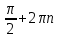 ; ; 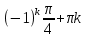 ; б) ; б) 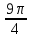 ; ; 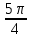 ; ; 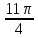 .▲ .▲Вар.13. а) Решите уравнение 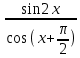 = =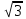 . .б) Укажите корни этого уравнения, принадлежащие промежутку [ 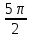 ; 4π). ; 4π).▼ а) Применим формулу 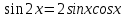 и формулу приведения и формулу приведения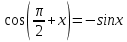 . .Уравнение примет вид: 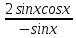 = =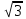 . Учитывая, что sinx ≠ 0, x ≠ πk, получим: . Учитывая, что sinx ≠ 0, x ≠ πk, получим:2cosx =- 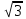 . .cosx =- 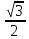 , x = , x = 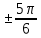 + 2πn. + 2πn.б) Отберем корни уравнения, принадлежащие промежутку [ 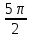 ; 4π), с помощью числовой окружности. ; 4π), с помощью числовой окружности.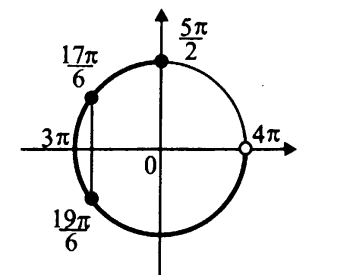 x = 2π + 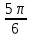 = = 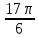 . .x = 4π - 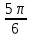 = = 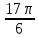 .. ..Отв: а) 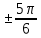 + 2πn; б) + 2πn; б) 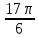 ; ; 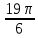 . .▲ Вар.17. а) Решите уравнение 8sinx + 4cos2x =7. б) Найдите корни уравнения, принадлежащие отрезку [ 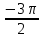 ; - ; -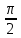 ]. ].▼ а) 8sinx + 4cos2x =7. 4(1 – sin2x) + 8sinx – 7 = 0. 4sin2x- 8sinx + 3 = 0. Пусть sinx = t, t 1, уравнение примет вид 4t– 8t + 3 = 0. t1,2 = 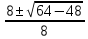 = = 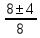 = 1 = 1 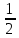 . .t1 = 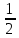 или t2 = или t2 = 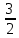 . t2 отбрасываем. . t2 отбрасываем.sinx = 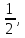 x = (-1)n x = (-1)n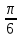 + πn. + πn.б) Найдем корни уравнения на отрезке [ 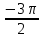 ; - ; -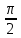 ]. ].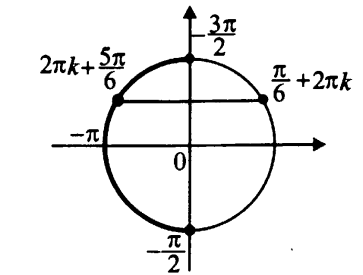 Это число 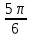 - 2π = - - 2π = -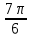 . .Отв: а) x = (-1)n 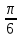 + πn.; б) - + πn.; б) -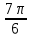 . .14) Вар.1. В прямоугольном параллелепипеде ABCDA1B1C1D1 стороны оснований АВ и ВС равны соответственно 8 и 5, а боковое ребро АА1 равно 4. На ребре A1B1 отмечена точка K, а на луче ВС – точка F, причем A1K = KB1 и BF = AB. Плоскость AKF пересекает ребро В1С1 в точке Р. а) Докажите, что B1Р : РС1 = 4 : 1. б) Найти площадь сечения параллелепипеда плоскостью AKF. ▼  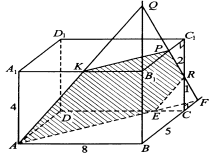 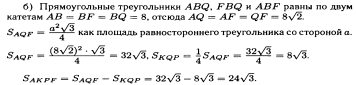  |
