Решение вариант ЕГЭ. Вариант Часть 1
 Скачать 1.17 Mb.
|
|
Вариант 1. Часть 1 1). Стоимость билета в музей составляет 500 рублей, а для льготной категории посетителей – 60% от полной стоимости. Группа состоит из 8 человек, двое из которых имеют право на приобретение льготного билета. Сколько рублей стоят билеты на всю группу? ▼ 500 руб. – полная стоимость билета; 5000,6 = 300 руб. – льготная стоимость билета. Все билеты стоят: 5006 + 3002 = 3600 руб. Отв: 3600.▲ 2) На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат – крутящий момент в Нм. 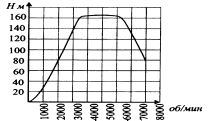 Чтобы автомобиль начал движение, крутящий момент должен быть не менее 80 Нм. Какое наименьшее число оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение? ▼ Выбираем точку с ординатой 80 к началу координат. С помощью рисунка находим соответствующую ординате точку на графике, из нее опускаем перпендикуляр на ось абсцисс и получаем точку, абсцисса которой равна 2000, это и есть наименьшее число оборотов двигателя. Отв: 2000.▲ 3) Вар.1. На клетчатой бумаге с размером клетки 11 изображен угол. Найти тангенс этого угла. 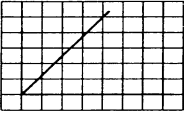  ▼ Проведем ВС перпендикулярно ОА и рассмотрим прямоугольный треугольник ОВС: tgBOA = tgBOC =  = 1,25.Отв: 1,25. ▲ Вар. 5. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см1 см. Ответ дайте в квадратных сантиметрах. ▼ Площадь ромба равна половине произведения его диагоналей. АС = 8, BD = 4, следовательно,  . 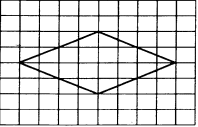 Отв: 16. ▲ 4). Вар.1. В сборнике билетов по физике всего 35 билетов, в 14 из них встречается вопрос по теме «Механика». Найти вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Механика». ▼Пусть выбор билета – исход, выбор билета, в котором есть вопрос по механике, - благоприятный исход. Общее число исходов n = 35, благоприятных исходов m = 14. По определению, вероятность  = 0,4.Отв: 0,4. ▲ Вар.5. Фабрика выпускает брюки. В среднем из 17 брюк 200 имеют скрытые дефекты. Найти вероятность того, что купленные брюки окажутся без дефектов. Результаты округлите до события сотых. ▼ Общее число исходов равно 200, неблагоприятных исходов 17. По определению, вероятность события, противоположного искомому («брюки имеют дефект»), равна  = 0,085. Вероятность события «брюки не имеют дефекта» равна 1 – 0,085 = 0,915 ≈ 0,92.Отв: 0,92. ▲ Вар.9. Вероятность того, что в случайный момент времени температура тела здорового человека будет отличаться от температуры 36,6°С не больше чем на 0,2°С, равна 0,964. Найти вероятность того, что в случайный момент времени у здорового человека температура окажется ниже, чем 36, 4°С, или выше, чем 36,8°С. ▼ Событие, «температура тела будет отличаться от температуры 36,6°С не больше, чем на 0,2°С, противоположно событию «температура окажется ниже, чем 36, 4°С, или выше, чем 36,8°С», поэтому искомая вероятность равна 1 – 0,964 = 0,036. Отв: 0,036.▲ Вар.13. Научная конференция проводится в 6 дней. Всего запланировано 80 докладов – первые четыре дня по 15 докладов, остальные распределены равномерно между пятым и шестым днями. На конференции планируется доклад профессора Л. Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора Л. Окажется запланированным на последний день конференции7 ▼ Найдем, сколько докладов запланировано на последний день конференции: (80 - 4·15):2 = 10 докладов. Будем считать экспериментом выбор порядкового номера профессора Д., эксперимент имеет 80 возможных исходов. Благоприятствуют указанному событию 10 исходов. Искомая вероятность равна 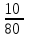 = 0,125.Отв: 0,125 ▲ Вар. 17. На экзамене по литературе школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Творчество Пушкина», равна 0,15, по теме «Творчество Лермонтова», равна 0,21. Вопросов, которые одновременно относятся к этим двум, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. ▼ Пусть событие А означает, что школьнику достанется вопрос по теме «Творчество Пушкина», событие В – вопрос по теме «Творчество Лермонтова». По условию Р(А) = 0,15, Р(В) = 0,21. По условию события А и В несовместны. Искомая вероятность события «школьнику достанется вопрос по одной из этих двух тем» равна Р(АВ) = Р(А) + Р(В) = 0,15 + 0,21 = 0,36. Отв: 0,36 ▲ 5) Вар.1. Найдите корень уравнения  .▼  ;  = 25, х = 25.Отв: 25.▲ Вар.5. Найдите корень уравнения x2 -19x + 90 = 0. Если уравнение имеет более одного корня, укажите меньший из них. ▼ x2 -19x + 90 = 0, х1,2 = 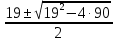 , х1 = 9, х2 = 10. Меньший из корней равен 9.Отв: 9.▲ 6) Вар.1. Найти площадь прямоугольной трапеции, основания которой равны 16 и 22, большая боковая сторона составляет с основанием угол 45°. ▼ Рассмотрим прямоугольную трапецию с основаниями ВС = 16, AD = 22, A = 90°, D = 45°. Проведем высоту CH. ABCH – прямоугольник, BC = AH = 16, тогда HD = 22 – 16 = 6.  Треугольник CDH прямоугольный и равнобедренный. HD = HC = 6. Площадь трапеции 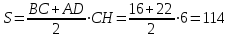 .Отв: 114. ▲ Вар.5. В треугольнике АВС А = 48°, С = 62°. На продолжении стороны АВ за точку В отложен отрезок ВD, равный стороне ВС. Найдите D треугольника ВСD. Ответ дайте в градусах.  ▼ Угол СВD является внешним углом треугольника АВС и равен сумме двух углов треугольника, не смежных с ним. СВD = А + С = 48° + 62° + 110°. Треугольник ВСD равнобедренный, его углы при основании равны: D = DСВ. Сумма углов треугольника равна 180°. Тогда D = (180° – 110°):2 = 35. Отв: 35. ▲ Вар.9. Стороны параллелограмма равны 8 и 16 см. Высота, опущенная на первую из этих сторон, равна 14. Найти высоту, опущенную на вторую сторону параллелограмма.  ▼ Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне. Для параллелограмма АВСD выполняется S = AB·DH = CB·DE. Получаем 16·DH = 8·14, DH = 7. Отв: 7. ▲ Вар. 13. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 14. Найти площадь этого треугольника.  ▼ Площадь треугольника можно найти как половину произведения двух его сторон на синус угла между ними  ·14 14·sin30° = 49.Отв: 49▲ Вар. 17. Площадь параллелограмма АВСDравна 324. Точа Р – середина стороны ВС. Найдите площадь трапеции АРСD. ▼ Точка Р – середина стороны ВС, поэтому РС = 0,5ВС. Обозначим h высоту параллелограмма, проведенного к стороне АD. Тогда площадь параллелограмма S = BC·h = 324. Площадь трапеции АРСD равна 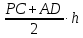 =  = =  = 0.75S = 243.  Отв: 243 ▲ 7) На рис. изображен график функции y = f(x) и касательная у нему в точке с абсциссой х0. Найти значение производной функции f(x) в точке х0. 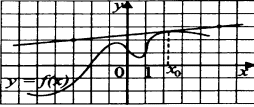 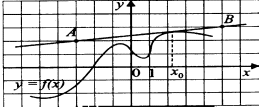 ▼ По рисунку определяем, что касательная проходит через точки В(5; 3) и А(-3; 2). Известно, что значение производной в точке х0 равно угловому коэффициенту касательной:  Отв: 0,125. ▲ 8) Найти площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 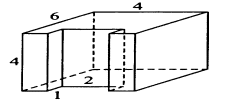 ▼ Площадь поверхности S многогранника состоит из площади оснований и площади боковой поверхности. Площадь одного из двух равных оснований равна разности площадей двух многоугольников, имеющих измерения 64 и 12, т.е. 64 - 21. Площадь боковой поверхности равна произведению периметра основания многогранника на его высоту. Отсюда, S = 2Sосн + Sбок = 2Sосн + Роснh, где Sосн , Росн, h соответственно – площадь основания, периметр основания и высота многогранника. S = 2(64 - 21) + (2 + 1 + 1 +6 + 4 + 6 + 1 + 1)4 = 132. Отв: 132. ▲ Часть 2 9) Вар.1. Найдите значение выражения  . ▼ =  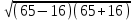=  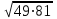= 79 = 63.Отв: 63. ▲ Вар.5. Найдите значение выражения 30,74·90,13. ▼ 30,74·(32)0,13 = 30,74·30,26 = 30,74+0,26 = 31 =3. Отв: 3. ▲ Вар.9. Найдите значение выражения 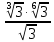 ▼ По свойству корней выполняются равенства:  , поэтому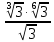 =  =  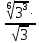=  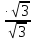= 1.Отв: 1. ▲ Вар.13 Найдите значения выражения 19a10a14:(5 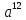 )2.▼19a10a1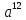4:(5 )2 = 19a10+14:(5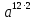 ) = = 0,76.Отв: 0,76▲ Вар.17. Найдите значение выражения 4log3(log5125). ▼4log3(log5 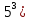 = 4log33 = 4·1 = 4.Отв: 4▲ 10) Независимое агентство намерено ввести рейтинг новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый отдельный показатель – целое число от -4 до 4. Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность – вдвое дороже, чем оперативность. Таким образом, формула приняла вид  . Найдите, каким должно быть А, чтобы издание, у которого все показатели максимальны, получило бы рейтинг 48.▼ Выразив А из формулы , получим 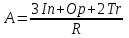 . Так как все показатели максимальны, то In = Op = Tr = 4, откуда  = 0,5.Отв: 0,5. ▲ 11) Вар.1. Из двух городов, расстояние между которыми 544 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 64 км/ч и 72 км/ч. ▼ Обозначим время автомобилей до встречи через х ч. Тогда первый автомобиль до встречи со вторым автомобилем пройдет 64х км, а второй автомобиль пройдет до встречи 72х км. Составим и решим уравнение: 64х + 72х = 544, 136х = 544, х = 4. Автомобили встретятся через 4 часа. Отв: 4. ▲ Вар.5. Из одной точки круговой трассы, длина которой равна 18 км, одновременно в одном направлении стартовали два автомобиля. Скорость одного из них 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найти скорость второго автомобиля. Ответ дайте в км/ч . ▼ Пусть х км/ч – скорость второго автомобиля; 40 минут =  часа. Составляем уравнение x = 63 км/ч.Отв: 63. ▲ Вар.9. В сосуд, содержащий 3 литра 14-процентного водного раствора некоторого вещества, добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора? ▼ Составляем таблицу:
Концентрация получившегося раствора 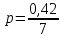 = 0,06, или 6%.Ответ: 6▲ Вар.13. В 2005 году в поселке проживало 55000 человек. В 2006 году в результате строительства новых домов, число жителей возросло на 6%, а в 2007 – на 10% по сравнению с 2006годом. Сколько человек стало проживать в поселке в 2007 году? ▼55000(1+0,06 + 0,1) = 1,16·55000 = 64130 человек. Отв: 64130▲ |