вариант. Вариант на 12.11. Вариант на 12. 11 Найдите корень уравнения 2
 Скачать 106.35 Kb.
|
|
Вариант на 12.11 1. Найдите корень уравнения  2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпала больше раз, чем орёл. 3. 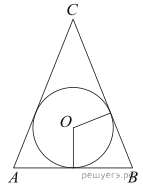 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника. 4. Найдите значение выражения  5. 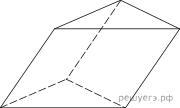 В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.6. На рисунке изображен график функции y = f(x), определенной на интервале (−9; 2). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −10. 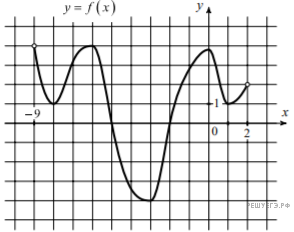 7. Груз массой 0,2 кг колеблется на пружине. Его скорость v меняется по закону  где t — время с момента начала колебаний, T = 24 с — период колебаний,  м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле  где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.8. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 9. 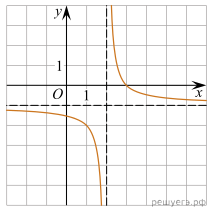 На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите  10. Вероятность того, что новый тостер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,8. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. 11. Найдите точку минимума функции  12. а) Решите уравнение  б) Найдите все корни этого уравнения, принадлежащие промежутку  13. В правильной треугольной пирамиде SABC сторона основания AB равна 4, а боковое ребро SA равно 5. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C. б) Найдите площадь многоугольника, являющегося сечением пирамиды SABC плоскостью α. 14. Решите неравенство:  15. В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы: — каждый январь долг возрастает на x% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. Найдите x, если известно, что наибольший платёж по кредиту составит не более 1,9 млн рублей, а наименьший — не менее 0,5 млн рублей. 16. Четырёхугольник ABCD вписан в окружность, причем сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке Е, а окружность — в точке F, причем H — середина AE. а) Докажите, что четырёхугольник BCFE — параллелограмм. б) Найдите площадь четырёхугольника ABCD, если известно, что AB = 3 и  17. Найдите все значения а. при каждом из которых уравнение  на промежутке  имеет более двух корней.18. Множество чисел назовём хорошим, если его можно разбить на два подмножества с одинаковой суммой чисел. а) Является ли множество {200; 201; 202; ...; 299} хорошим? б) Является ли множество {2; 4; 8; ...; 2100} хорошим? в) Сколько хороших четырёхэлементных подмножеств у множества {1; 2; 4; 5; 7; 9; 11}? |