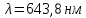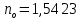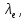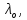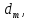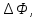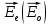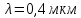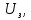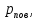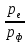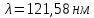ФИЗИКА РГР ВСЕ ЗАДАЧИ. Вариант задача 1
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
5 - ВАРИАНТЗадача 1 Параллельный пучок света с длиной волны λ = 643,8 нм падает по нормали на пластинку из кристалла кварца в половину длины волны перпендикулярно её оптической оси. Показатели преломления для необыкновенного и обыкновенного лучей составляют соответственно 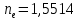 и и 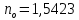 . Определить: 1) длины волн этих лучей в кристалле; 2) минимальную толщину пластинки; 3) разность фаз между обыкновенным и необыкновенным лучами на выходе из пластинки; 4) уравнение траектории конца результирующего светового вектора для луча на выходе пластинки. Обосновать, какой тип поляризации будет наблюдаться у луча на выходе из пластинки. Изобразите на рисунке ход для необыкновенного и обыкновенного лучей, покажите тип поляризации этих лучей. . Определить: 1) длины волн этих лучей в кристалле; 2) минимальную толщину пластинки; 3) разность фаз между обыкновенным и необыкновенным лучами на выходе из пластинки; 4) уравнение траектории конца результирующего светового вектора для луча на выходе пластинки. Обосновать, какой тип поляризации будет наблюдаться у луча на выходе из пластинки. Изобразите на рисунке ход для необыкновенного и обыкновенного лучей, покажите тип поляризации этих лучей.
Определение показателя преломления: 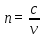 где 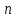 — абсолютный показатель преломления, — абсолютный показатель преломления, 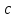 — скорость света в вакууме, — скорость света в вакууме, 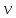 — скорость света в среде. Он отражает то, во сколько раз медленнее свет распространяется в среде, чем в вакууме. С другой стороны, зная связь скорости света в среде и ее длины волны: — скорость света в среде. Он отражает то, во сколько раз медленнее свет распространяется в среде, чем в вакууме. С другой стороны, зная связь скорости света в среде и ее длины волны: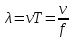 где 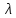 — длина волны, — длина волны, 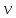 — скорость света в среде, — скорость света в среде, 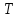 — период колебаний, f — частота, получаем связь коэффициента преломления и длины волны: — период колебаний, f — частота, получаем связь коэффициента преломления и длины волны: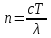 Видно, что в числителе стоит длина волны света в вакууме ( 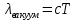 ), а в знаменателе длина волны в среде. Выражая искомые длины волн: ), а в знаменателе длина волны в среде. Выражая искомые длины волн: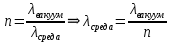 получаем для обыкновенного и необыкновенного лучей: 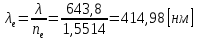 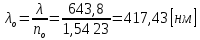 Оптическая длина пути 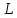 в среде с показателем преломления в среде с показателем преломления 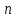 равна произведению геометрической длины пути равна произведению геометрической длины пути 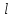 , пройденного светом, на показатель преломления , пройденного светом, на показатель преломления 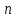 : :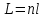 В нашей задаче геометрическая длина пути — это и есть искомая толщина пластинки. Также из условия (пластинка в половину длины волны) ясно, что разность хода (разность оптических длин преломленного (необыкновенного) и непреломленного (обыкновенного)) лучей составляет половину исходной длины волны: 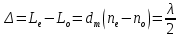 Выражаем искомую величину: 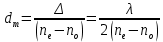 Подставляем значения: 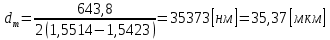 Длина волны — расстояние между точками с одинаковой фазой. Это значит, что разность фаз между точками, расстояние между которыми равно длине волны, составляет 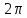 . Это позволяет составить простую пропорцию и выразить искомую величину: . Это позволяет составить простую пропорцию и выразить искомую величину: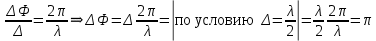 Если свет распространяется перпендикулярно оптической оси, то поляризацию можно разложить на две проекции — параллельную оптической оси и перпендикулярную. Эффективный показатель преломления будет разным для света двух ортогональных поляризаций, и при прохождении через слой (пластинку) материала может наблюдаться сдвиг по фазе между двумя компонентами. Если исходная поляризация линейная и ориентирована либо полностью вдоль, либо полностью перпендикулярно оптической оси, то на выходе из пластинки она не изменится. Однако, если исходно свет поляризован под углом к оптической оси, либо поляризация эллиптическая или циркулярная, то при прохождении через пластинку из одноосного кристалла поляризация может измениться из-за сдвига по фазе между компонентами. По условию свет изначально имел круговою поляризацию, значит обыкновенный и необыкновенный лучи будут линейно поляризованы и перпендикулярны друг другу. Введем координатные оси и, учитывая поляризацию света, запишем уравнение траектории конца светового вектора для необыкновенного луча на выходе пластинки: 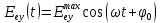 Где 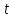 — время, — время, 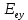 — — 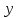 -вая компонента вектора напряженности (других компонент нет, так как свет так линейно поляризован), -вая компонента вектора напряженности (других компонент нет, так как свет так линейно поляризован), 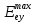 — амплитуда, — амплитуда, 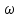 — циклическая частота, — циклическая частота, 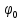 — начальная (в момент времени t=0) фаза. — начальная (в момент времени t=0) фаза.Для обыкновенного луча необходимо учесть, что он поляризован перпендикулярно и имеет сдвиг фазы: 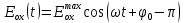 Сдвиг фазы на 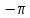 даёт смену знака гармонической функции: даёт смену знака гармонической функции: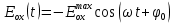 Выразим 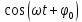 из обоих формул, получим искомое уравнение траектории: из обоих формул, получим искомое уравнение траектории: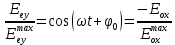  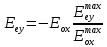 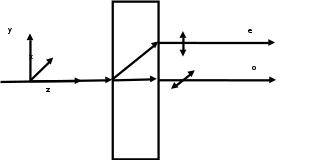 Ответ:𝜆𝑒=414,98нм;𝜆о=417,43нм;𝑑𝑚=35,37мкм;∆Ф=𝜋;𝐸𝑒𝑦=−𝐸𝑒𝑚𝑎𝑥/𝐸𝑜𝑚𝑎𝑥*𝐸𝑜𝑥 Задача 2 Работа выхода электрона из металла 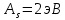 . Поверхность металла облучается фотонами с длиной волны . Поверхность металла облучается фотонами с длиной волны 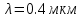 . Определить задерживающее напряжение . Определить задерживающее напряжение  для этого опыта. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона ( для этого опыта. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона (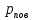 ). Во сколько раз отличается импульс выбитого электрона ( ). Во сколько раз отличается импульс выбитого электрона (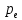 ) от импульса фотона ( ) от импульса фотона (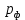 ), который падает на поверхность? Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ВАХ ток насыщения ), который падает на поверхность? Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ВАХ ток насыщения  и задерживающий потенциал ( и задерживающий потенциал ( ). ).
Уравнение фотоэффекта — закон сохранения энергии, который говорит, что энергия кванта излучения (фотона) идет на преодоление электроном работы выхода и приобретение им кинетической энергии. 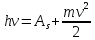 где 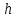 — постоянная Планка, — постоянная Планка,  — частота излучения, их произведение это энергия фотона — частота излучения, их произведение это энергия фотона 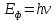 , , 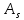 — работа выхода, энергия, которую надо потратить, чтобы электрон покинул материал, — работа выхода, энергия, которую надо потратить, чтобы электрон покинул материал, 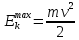 — максимальная кинетическая энергия электрона. — максимальная кинетическая энергия электрона.Запирающее напряжение — это обратное напряжение, которое нужно подать на анод и катод, чтобы ток, который появляется в ходе фотоэффекта прекратился. Работа этого поля должна компенсировать кинетическую энергию электронов. Связь работы и напряжения: 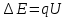 где где 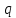 – заряд, – заряд, 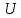 – напряжение, – напряжение, 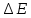 – приращение энергии, работа. В нашем случае речь идет об электроне поэтому – приращение энергии, работа. В нашем случае речь идет об электроне поэтому 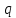 заменим на заменим на 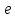 – заряд электрона. Тогда получим: – заряд электрона. Тогда получим: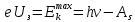 Связь длины волны, частоты и скорости: 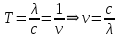 Выражаем искомую величину, подставляем значения (важно заметить, что работа выхода нам дана в электрон-вольтах, соответственно, ее пересчитываем): 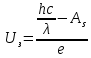 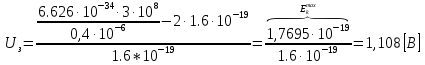 По закону сохранения импульса, поверхность испытывает “отдачу” равную импульсу выбитого электрона. 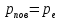 Кинетическую энергию электрона мы нашли при ответе на прошлый вопрос. Через неё найдем импульс электрона и соответственно искомую величину: 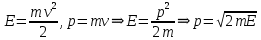 В нашем случае 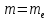 — масса электрона. Таким образом: — масса электрона. Таким образом: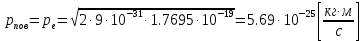 Импульс фотона: 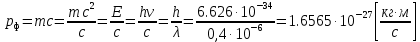 крипч крипч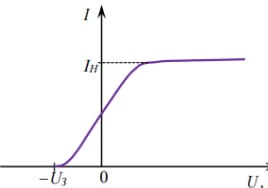 Напряжении, при котором сила тока в фотоэлементе обращается в ноль, 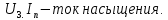 держивающим напряжением 𝑼з. 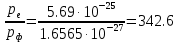 Ответ: 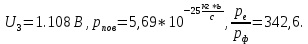 Задача 3 Атомарный водород, находящийся в основном состоянии, облучается монохроматическим светом с длиной волны 121,58 нм и переходит в возбужденное состояние. Определить радиус 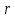 боровской орбиты этого возбужденного состояния. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней переход из основного в возбужденное состояние. боровской орбиты этого возбужденного состояния. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней переход из основного в возбужденное состояние.
Энергия фотона расходуются на возбуждение атома. Разность между энергией возбужденного состояния и основного равно энергии фотона. Энергия основного состояния, это энергия, которую требуется потратить для полной ионизации газа. 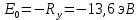 , где , где 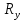 — постоянная Ридберга: — постоянная Ридберга: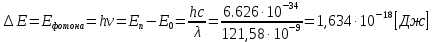 Для удобства пересчитаем в электрон-вольтах: 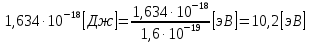 Энергия 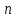 –того состояния: –того состояния: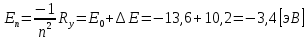 Отсюда: 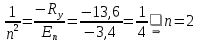 Радиус атома в -том состоянии: 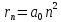 где 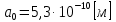 — боровский радиус (радиус ближайшей к ядру орбиты электрона). — боровский радиус (радиус ближайшей к ядру орбиты электрона).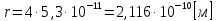 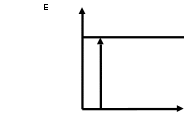 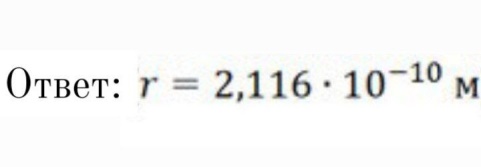 |