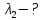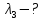ФИЗИКА РГР ВСЕ ЗАДАЧИ. Вариант задача 1
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
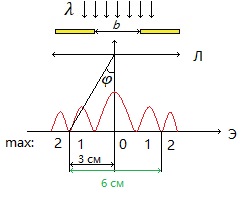
6 - ВАРИАНТМонохроматический свет падает нормально на щель шириной 10 мкм. За щелью находится тонкая линза с оптической силой 4Дптр. В фокальной плоскости линзы расположен экран. Найти длину волны света 𝜆, если расстояние между симметрично расположенными минимумами второго порядка равно 6 см. Приведите рисунок для схемы установки. Изобразите дифракционную картину интенсивности света на экране. Пронумеруйте все дифракционные максимумы, которые могут быть видны на экране. (𝜆 = 595,7нм)
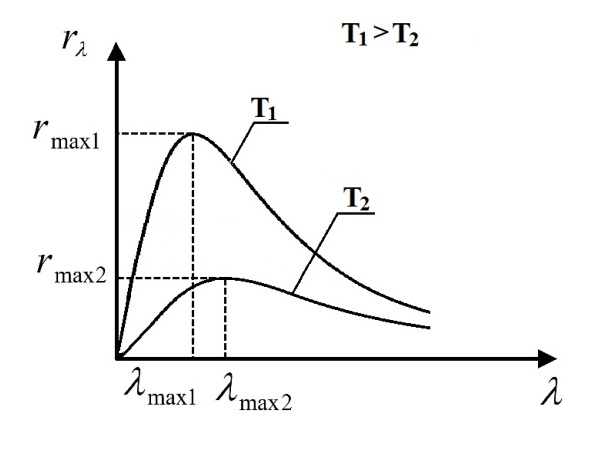
Нам нужно найти длину волны 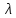 . Ее мы можем выразить из условия наблюдения дифракционного минимума: . Ее мы можем выразить из условия наблюдения дифракционного минимума: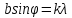 1.1 1.1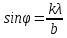 Где 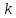 , порядок дифракционного минимума, у нас по условию , порядок дифракционного минимума, у нас по условию 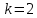 . .Фокусное расстояние линзы определим из ее оптической силы: 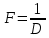 1.2 1.2 Из формул 1.1 и 1.2 мы можем вывести формулу для расстояния от центра дифракционной картины до минимума второго порядка: 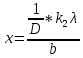 1.3 1.3Нам дано расстояние между симметрично расположенными минимумами второго порядка = 6 см, но для  нам нужно расстояние от центра дифракционной картины до минимума второго порядка, которое исходя из рисунка является нашим катетом. нам нужно расстояние от центра дифракционной картины до минимума второго порядка, которое исходя из рисунка является нашим катетом. Отсюда: 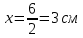 . .Выразим из 1.3 длину волны λ: 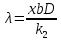 1.4 1.4Подставим числовые значения: 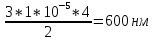 Ответ: длина волны λ = 600 нм. Температура абсолютно черного тела увеличилась в 1,5 раза, в результате чего длина волны 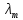 , на которую приходится максимум энергии излучения, изменилась на , на которую приходится максимум энергии излучения, изменилась на 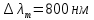 . Определить начальную . Определить начальную 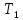 и конечную и конечную 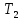 температуру тела. Во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом? Рисунком поясните график распределения энергии в спектре излучения абсолютно чёрного тела, укажите для данных температур положение температуру тела. Во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом? Рисунком поясните график распределения энергии в спектре излучения абсолютно чёрного тела, укажите для данных температур положение 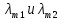 . ( . (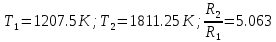 ) )
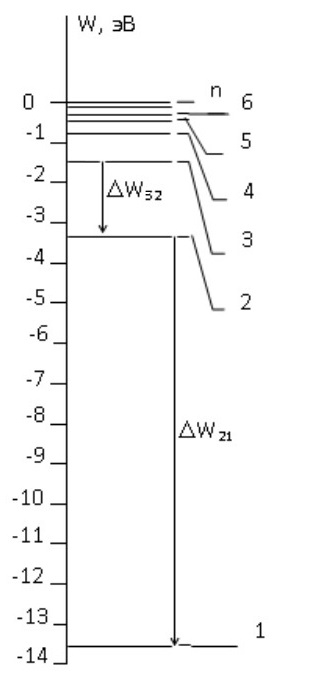
Воспользуемся законом смещения Вина: длина волны, на которую приходится максимум излучательной способности а.ч.т. 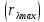 обратно пропорционален абсолютной температуре этого тела. Для любого а.ч.т. постоянная обратно пропорционален абсолютной температуре этого тела. Для любого а.ч.т. постоянная 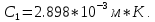 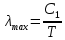 2.1 2.1 По условию задачи температура абсолютно черного тела увеличилась в 1.5 раза: 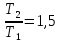 2.2 2.2Следовательно: 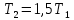 2.3 2.3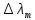 определяется как разница между определяется как разница между 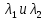 : :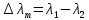 2.4 2.4Выразим  и и  : :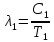 2.5 2.5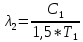 2.6 2.6Подставим 2.5 и 2.6 в 2.4: 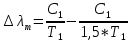 2.7 2.7Выразим температуру первого тела 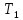 , для этого для начала приведем , для этого для начала приведем 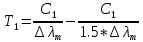 2.8 2.8Подставим наши данные: 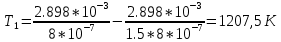 Зная 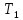 , мы можем найти , мы можем найти 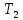 , подставив значение , подставив значение 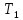 в 2.3: в 2.3: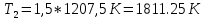 Согласно закону Стефана – Больцмана, энергетическая светимость R абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. 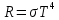 2.9 2.9где 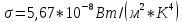 – постоянная Стефана-Больцмана. – постоянная Стефана-Больцмана.Определим, во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом. Для этого определим отношение 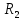 к к 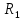 . .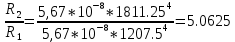 Ответ: 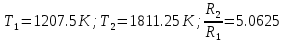 Атомарный водород, находящийся в некотором возбужденном состоянии, переходит в основное состояние. При этом радиус боровской орбиты уменьшается в 9 раз. Определить все длины волн  , излучаемые при переходе из первоначального состояния в основное, имея виду, что переход в основное состояние может происходить через промежуточные состояния. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней все переходы из возбужденного в основное состояние, включая промежуточные переходы. ( , излучаемые при переходе из первоначального состояния в основное, имея виду, что переход в основное состояние может происходить через промежуточные состояния. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней все переходы из возбужденного в основное состояние, включая промежуточные переходы. (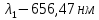 ; ; 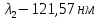 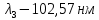
Определим радиус боровской орбиты в возбужденном состоянии. Сила Кулона, действующая на электрон в водородоподобном атоме со стороны ядра, является центростремительной силой. 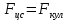 3.1 3.1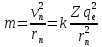 где 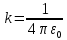 – коэффициент в законе Кулона, – коэффициент в законе Кулона, 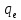 – величина заряда электрона, – величина заряда электрона, 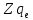 – величина заряда ядра водородоподобного атома. Выразим скорость из постулата стационарных состояний: – величина заряда ядра водородоподобного атома. Выразим скорость из постулата стационарных состояний: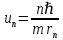 3.2 3.2Подставим выражение для скорости в 3.1: 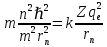 Получим зависимость радиуса орбиты электрона 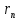 от номера орбиты n: от номера орбиты n: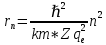 3.3 3.3Заметим, что дробь, стоящая перед квадратом номера орбиты, является набором констант и соответствует радиусу орбиты электрона при n = 1. Тогда для атома водорода при Z=1 можно записать: 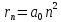 3.4 3.4где  – боровский радиус. – боровский радиус.Определим боровский радиус в возбужденном состоянии. По условию, боровский радиус уменьшился в 9 раз, то есть изначально (в возбужденном состоянии), он был в 9 раз больше, отсюда, 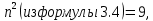 следовательно, n = 3. следовательно, n = 3.Делаем вывод, что изначально возбужденный атом находился на 3 уровне. В простейшем случае, в атоме водорода имеется один единственный электрон, который является валентным электроном. Значения энергии для электрона в атоме водорода определяются формулой: 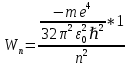 3.5 3.5Здесь первая дробь представляет собой набор констант, а n - главное квантовое число. Обозначим: 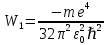 3.6 3.6Тогда 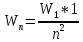 3.7 3.7Здесь 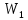 – энергия основного состояния электрона в атоме водорода. Полезно запомнить, что – энергия основного состояния электрона в атоме водорода. Полезно запомнить, что 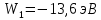 . Поэтому формулу (3.7) часто пишут в виде: . Поэтому формулу (3.7) часто пишут в виде: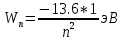 3.8 3.8В случае внешних воздействий атом, т.е. фактически его электрон, может получить дополнительную энергию и перейти в одно из возбужденных состояний, энергия которых больше, чем энергия основного состояния. Такие переходы называют переходами на более высокие энергетические уровни. Из возбужденных состояний атом спонтанно, т.е. самопроизвольно, переходит в основное состояние или на один из более низких энергетических уровней. При этом атом излучает в окружающее пространство энергию: 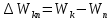 3.9 3.9Здесь 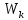 – энергия атома в исходном состоянии, а – энергия атома в исходном состоянии, а 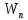 – энергия атома в конечном состоянии. Энергия – энергия атома в конечном состоянии. Энергия 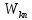 излучается в виде кванта электромагнитного излучения излучается в виде кванта электромагнитного излучения 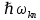 , так что , так что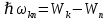 3.10 3.10Соотношение 3.10 часто называют правилом частот. Из соотношений 3.5 и 3.10 следует, что частота излучения равна: 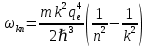 (3.10) (3.10)Выразив циклическую частоту 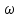 через длину волны λ, можно записать, что: через длину волны λ, можно записать, что: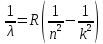 3.11 3.11Здесь величина 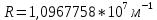 называется постоянной Ридберга. называется постоянной Ридберга.Из формулы 3.11 мы можем легко выразить длину волны: 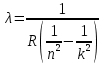 3.12 3.12Мы выяснили, что изначально наш атом был на 3 уровне (n=3). Подставим значения наших уровней в 3.12: 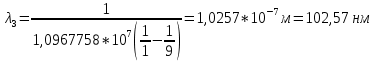 Далее он перешел на второй уровень: 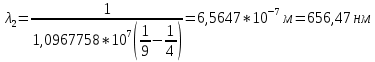 А затем спустился на первый: 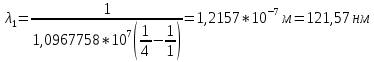 Ответ: 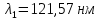 ; ; 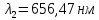  |

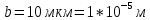
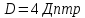
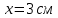
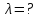
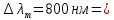
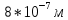
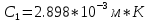
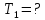
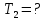
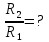
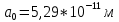
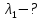 ;
;