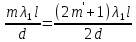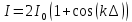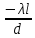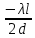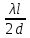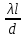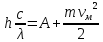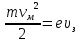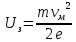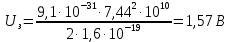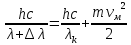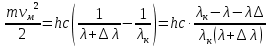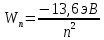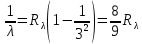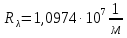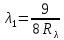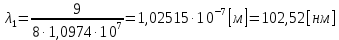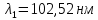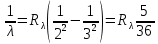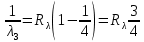ФИЗИКА РГР ВСЕ ЗАДАЧИ. Вариант задача 1
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
1 - ВАРИАНТ1. В опыте Юнга вначале рассматривается излучение с длиной волны λ1 = 0,7 мкм, а затем с λ2. Определите значение длины волны λ2, если шестая светлая полоса в первом случае совпадает с девятой темной полосой во втором случае. Рисунком поясните схему опыта Юнга, укажите на рисунке распределение интенсивности света на экране. Опыт проводится в вакууме. (𝜆2 = 494,1нм) Дано: 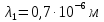 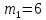 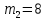 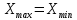 Найти: 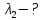 Решение: 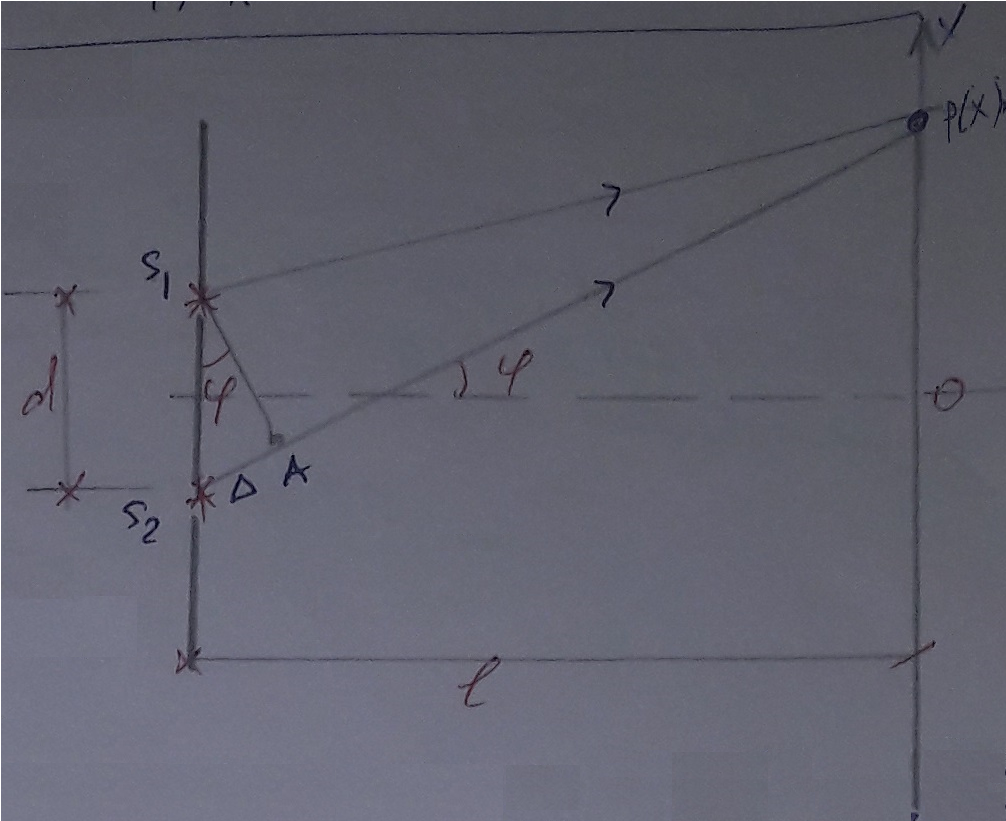 Где 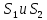 – когерентны, источники света – когерентны, источники светаd – расстояние между ними Расстояние от источника до экрана h>>d 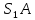 является волновым фронтом. Поэтому разность хода образуется на расстояние | является волновым фронтом. Поэтому разность хода образуется на расстояние |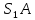 | : | : 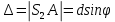 , т.к. 𝛗<<1, , т.к. 𝛗<<1, 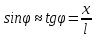 , , 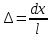 . .Светлая полоса возникает если «∆» содержит целое число длины волн: 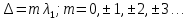 - целое число. - целое число.Тёмная полоса возникает если «∆» содержит нечетное число полудлин волн; 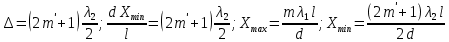 . .По условию 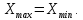
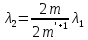 Центральную светлую полосу не будем считать. Тогда m=6. Первый минимум соответствует 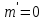 . . 9-й минимум соответствует 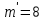 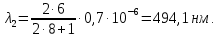 Если интенсивность источников равны 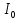 то интенсивность света в точке наблюдения то интенсивность света в точке наблюдения 
Где, 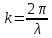 – волновой центр, – волновой центр,∆ - оптическая разность хода. 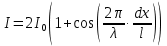 I(x) будет изменятся по закону косинуса вокруг 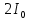
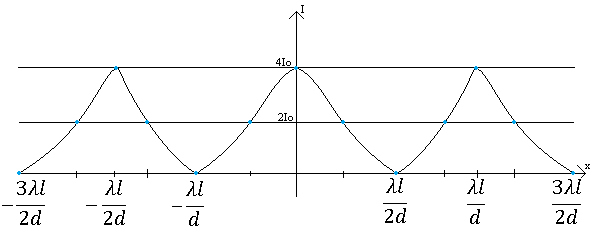 Ответ: 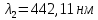 2. Красная граница фотоэффекта рубидия λ0=0,81 мкм. Определить скорость фотоэлектронов при облучении рубидия монохроматическим светом с длиной волны λ=0,4 мкм. Какую задерживающую разность потенциалов Uз надо приложить к фотоэлементу, чтобы прекратить фототок? На сколько изменится задерживающая разность потенциалов ΔUз при увеличении длины волны падающего света на Δλ=200 нм? Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ВАХ ток насыщения и задерживающий потенциал. (𝜐 = 7.44 ∙ 105м/с; 𝑈з = 1.57 В; ∆𝑈 = 1.036 В) Дано: 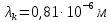 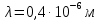 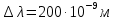 Найти: 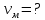 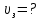 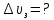 Решение: По закону Эйнштейна для фотоэффекта:
где 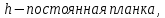 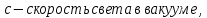 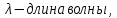 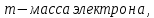 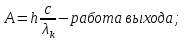 Производим замену переменных и запишем формулу: 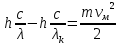 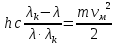 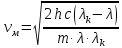 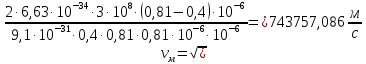 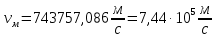 По теореме о кинетической энергии, изменение кинетической энергии равно работе электрических сил:
При увеличении длины волны на  формула Эйнштейна будет таким: формула Эйнштейна будет таким:
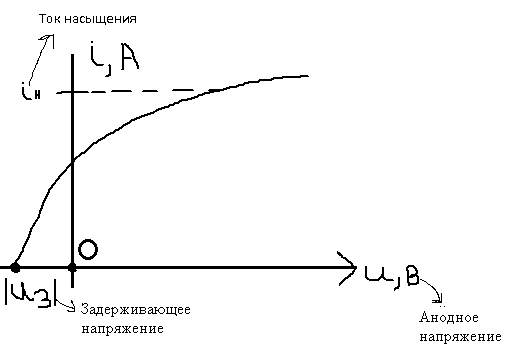 Зависимость силы фототока от анодного напряжения, ( 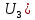 – задерживающее напряжение. – задерживающее напряжение.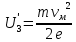 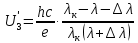  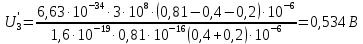 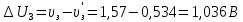 Ответ: 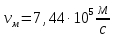 ; ; 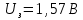 ; ; 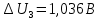 . .3. Свободный электрон, имея кинетическую энергию 15 эВ, неупруго столкнулся с атомом водорода, находящимся в основном состоянии, и отскочил от него, потеряв часть энергии. Энергия электрона после столкновения оказалась 2.91 эВ. Определить длины волн, которые может излучить атом водорода после столкновения с электроном. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней все переходы между уровнями, которые могут произойти после столкновения. (𝜆1 = 102.58 нм; 𝜆2 = 121.58 нм; 𝜆3 = 656.51 нм) Дано: T=15 эВ 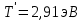 Найти: 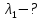 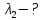 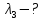 Решение: Энергия электрона в атоме водорода определяется формулой
Где -13,6 эВ – энергия основного состояния, n – главное квантовое число. После получения дополнительной энергии 12,09 эВ электрон с основного состояния (h=1) перейдёт в состоянии с «n»: 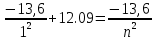 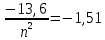 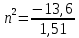 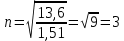 n=3, то электрон перейдёт в состояние с n=3. 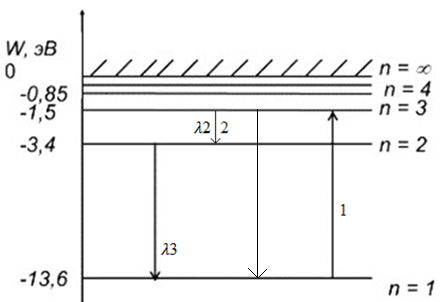 По формуле Бора соответствующее излучение имеет длину волны:
Постоянная Ридберга:
После столкновения может произойти переход: 32 с
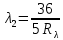 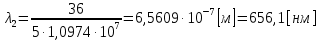 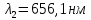 И переход 2 1 с:
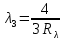 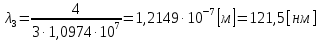 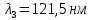 Ответ: 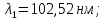 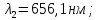 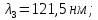 |