Задачи_резервирование. Вероятность безотказной работы системы при раздельном дублировании и равнонадежных элементах равна
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
1. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента ср =10000Т ч. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти среднее время безотказной работы системы Cр =1000Т , а также частоту отказов с t и интенсивность отказов с t в момент времени t = 50 ч в следующих случаях: а) нерезервированной системы, б) дублированной системы при постоянно включенном резерве. Ответ:  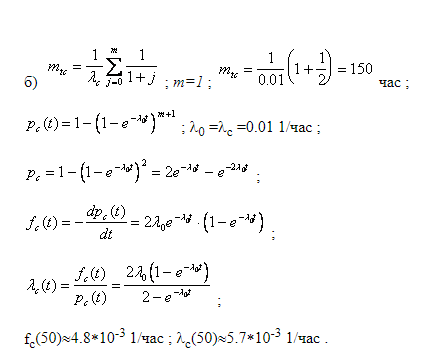 2. Нерезервированная система управления состоит из n=5000 элементов. Для повышения надежности системы предполагается провести общее дублирование элементов. Чтобы приближенно оценить возможность достижения заданной вероятности безотказной работы системы Рс(t) = 0,9 при t =10 ч, необходимо рассчитать среднюю интенсивность отказов одного элемента при предположении отсутствия последействия отказов. Ответ Вероятность безотказной работы системы при раздельном дублировании и равнонадежных элементах равна:  3. Вероятность безотказной работы преобразователя постоянного тока в переменный в течение времени t=1000 ч равна 0,95, т. е. Р(1000) = 0,95. Для повышения надежности системы электроснабжения на объекте имеется такой же преобразователь, который включается в работу при отказе первого (режим ненагруженного резерва). Требуется рассчитать вероятность безотказной работы и среднее время безотказной работы системы, состоящей из двух преобразователей, а также определить частоту отказов с t и интенсивность отказов с t системы Ответ В рассматриваемом случае кратность резервирования m = 1. Используя формулу (5.9), получим   4. Основная функционально-необходимая система представляет собой последовательное (в смысле надежности) соединение элементов. Число элементов n = 4. Интенсивность отказов у каждого из элементов равна = 0,210–3 . Определить показатели надежности системы без резервирования и при различных методах резервирования на момент времени 1000 час, при кратности резервирования m = 1, m = 2. Сравнить эффективность методов резервирования. Ответ     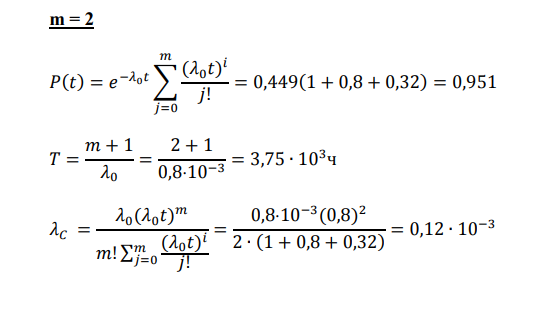 . . Основная функционально-необходимая система представляет собой последовательное (в смысле надежности) соединение элементов. Число элементов n = 4. Интенсивность отказов у каждого из элементов равна = 0,210–3 . Определить показатели надежности системы без резервирования и при различных методах резервирования на момент времени 1000 час, при кратности резервирования m = 1, m = 2. Сравнить эффективность методов резервирования. Ответ 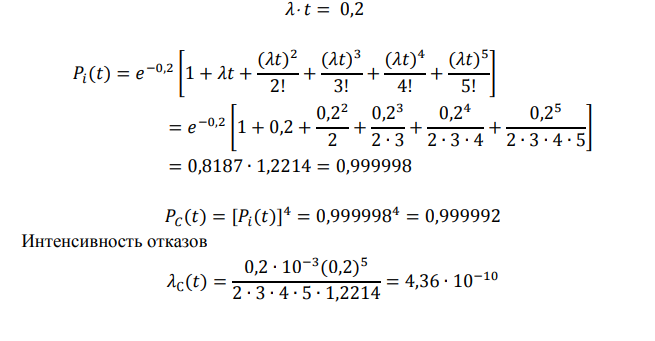 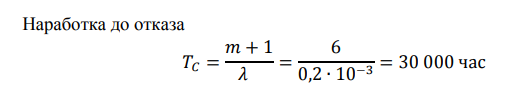 5. Система имеет кратность раздельного резервирования замещением с целой кратностью m = 5. Основная нерезервированная система содержит четыре равнонадежных элемента с логически последовательным соединением. Интенсивность отказов одного элемента λ = 0,210-3 . Определить характеристики надежности системы за 1000 ч Ответ Определим интенсивность отказов основной системы по формуле  6. Система построена из 4 однотипных блоков, которые имеют интенсивность отказов λ = 0,210-3 . Определить показатели надежности системы за 1000 час работы, если в скользящем «холодном» резерве находится: 1 такой же блок, 2 таких же блока. Резервные блоки могут заменить в случае отказа любой из отказавших блоков Ответ   7. Система имеет общее резервирование с дробной кратностью и постоянно включенным резервом. Система работоспособна, если работоспособны не менее 2-х элементов из 3-х. Определить показатели надежности для t = 1000 час, если интенсивность отказов элементов λ = 0,210- 3 . Ответ:  8. Система имеет кратность общего резервирования m = 5. Основная нерезирвированная система содержит четыре равнонадежных элемента с логически последовательным соединением. Интенсивность отказов одного элемента λ = 0,210-3 . Определить характеристики надежности системы за 1000 ч Ответ   9. Определить характеристики надежности системы при кратности раздельного резервирования каждого элемента m = 5. Интенсивность отказов одного элемента λ = 0,210-3 . Определить характеристики надежности системы за 1000 ч. Ответ     10. Найти среднюю наработку до первого отказа и вероятность безотказной работы устройства, структурная схема которого приведена на рис При его двукратном резервировании, если р1 = 0,9; p2 = 0,7; tраб = 100 ч Ответ. |
